
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
28-10-2024 - Analytic Geometry - Matrix Operations [EN]-[IT]
With this post I would like to give a brief instruction regarding the topic mentioned in the subject
(code notes: X_088)
Matrix Operations
The main operations that are performed with matrices are 3.
Given a matrix A, these elementary operations can be performed.
I-Exchange of two rows of A
II-multiplication of a row of A by an element Y that belongs to K
III-replacement of a row of A with the sum of the row itself and a multiple of another row.
Example
Let's consider the following matrix.
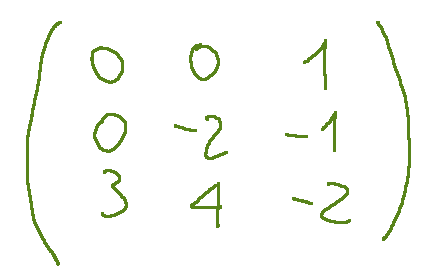
Exercise 1
Let's try to perform an elementary operation of type II, that is, multiply the third row by -3/4
To obtain the result, we must multiply each term of the third row by -¾ and we will obtain the correct result. Below is the matrix following the elementary operation requested.
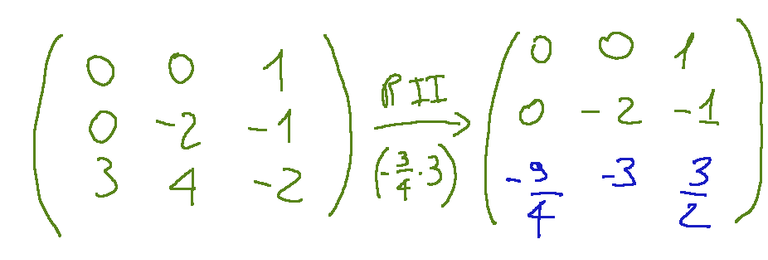
Exercise 2
Let's now try to perform a type III operation. That is, we replace the first row with the sum of the row itself and the second row multiplied by -2
Let's perform the elementary type III operation. We take the first row and add it to the second row multiplied by -2. The result will replace the first row.
What I have just described translates into this writing
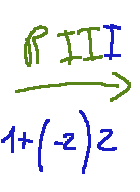
This is the result of the exercise
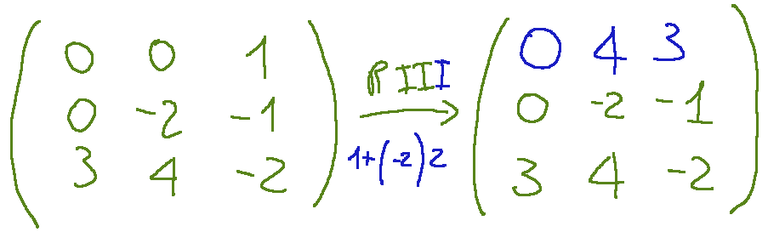
Exercise 3
Perform a type I operation. Swap the first with the second column
The result will be the following.
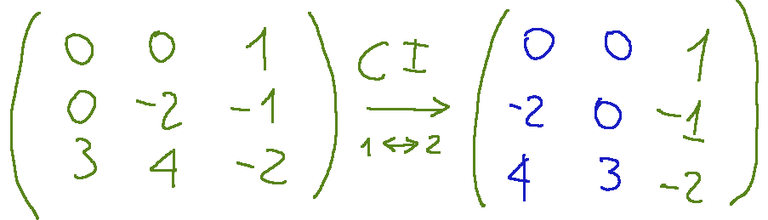
Conclusions
When we manage matrices we have at our disposal 3 elementary operations called type I, II and III
Question
Have you ever performed elementary operations on matrices?

[ITALIAN]
28-10-2024 - Geometria analitica - Operazioni con le matrici [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_088)
Operazioni con le matrici
Le principali operazioni che si effettuano con le matrici sono 3.
Data una matrice A si possono effettuare queste operazioni elementari.
I-Scambio di due righe di A
II-moltiplicazione di una riga di A per un elemento Y che appartiene a K
III-sostituzione di una riga di A con la somma della riga stessa e di un multiplo di un’altra riga.
Esempio
Prendiamo in considerazione la seguente matrice.
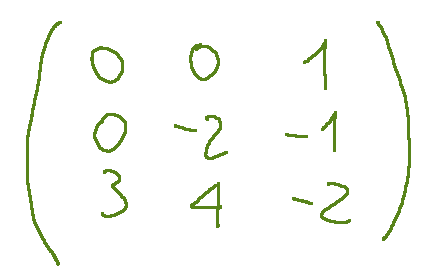
Esercizio 1
Proviamo ad effettuare un operazione elementare di tipo II, cioè moltiplicare la terza riga per -3/4
Per ottenere il risultato dobbiamo moltiplicare ogni termine della terza riga per -¾ ed otterremo il risultato corretto. Qui di seguito la matrice a seguito dell’operazione elementare richiesta.
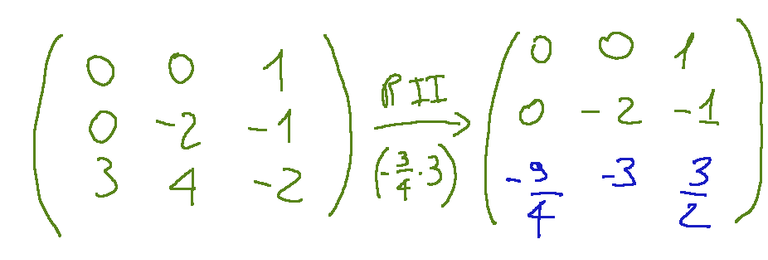
Esercizio 2
Proviamo ora ad effettuare un'operazione di tipo III. Cioè sostituiamo la prima riga con la somma della riga stessa e della seconda riga moltiplicata per -2
Andiamo ad effettuare l’operazione elementare di tipo III. Prendiamo la prima riga e la sommiamo alla seconda riga moltiplicata per -2. Il risultato andrà a sostituire la prima riga.
Questo che ho appena descritto si traduce in questa scrittura
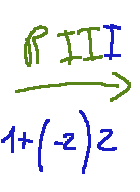
Questo il risultato dell'esercizio
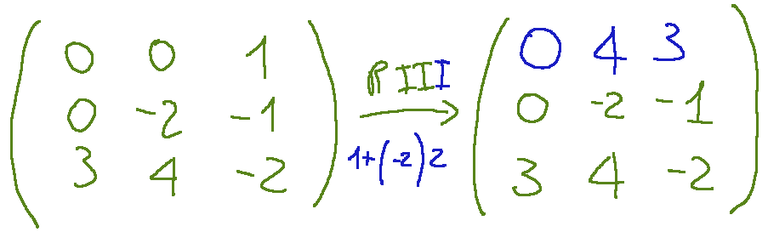
Esercizio 3
Effettuare un'operazione di tipo I. Scambiare la prima con la seconda colonna
Il risultato sarà il seguente.
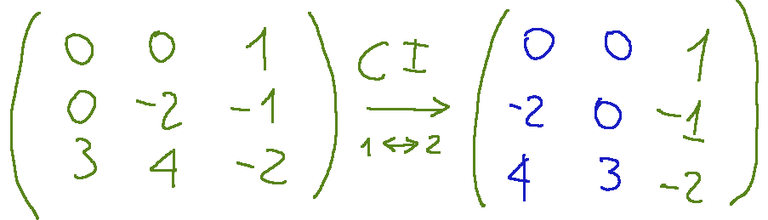
Conclusioni
Quando gestiamo delle matrici abbiamo a nostra disposizione 3 operazioni elementari dette di tipo I, II e III
Domanda
Avete mai eseguito delle operazioni elementari sulle matrici?
THE END



