En este post queremos deducir la técnica para derivar el cociente de dos de funciones reales de variable real continuas y diferenciables, g y h
In this post we want to deduce the technique to derive the quotient of two of continuous and differentiable real functions of real variable, g and h.
Esto es:
Dadas las funciones diferenciables g y h, con dominio en 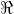.gif)
( el conjunto de los números reales), se quiere determinar y aplicar en ejemplos la Técnicas para derivar la función f definida por f(x)=g(x)/h(x).
That is:
Given differentiable functions g and h, with domain in( the set of real numbers), we want to determine and apply in examples the Techniques for deriving the function f defined by f(x)=g(x)/h(x).
Comencemos // Let's start
Usemos la definición de derivada para deducir la técnica, esto es:// Let us use the definition of derivative to derive the technique, that is:
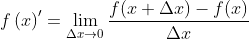.gif)
Donde f(x)=g(x)/h(x), por lo que nuestra expresión anterior, queda así:// Where f(x)=g(x)/h(x), so our previous expression, remains as follows:
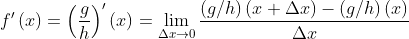.gif)
Apliquemos la definición de cociente de funciones en la expresión anterior:// Let us apply the definition of quotient of functions in the previous expression:
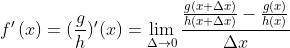.gif)
Desarrollando, nos queda://Developing, we are left with:
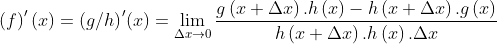.gif)
Restando y sumando en el numerador g(x).h(x), nos queda así: // Subtracting and adding in the numerator g(x).h(x), we get:
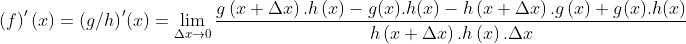.gif)
Aplicando factor común, nos queda así :// Applying the common factor, we are left with :
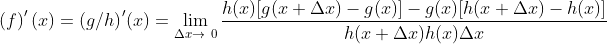.gif)
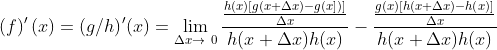.gif)
Con la finalidad de simplificar la demostración, cuyo resultado es evidente, hagamos las siguientes consideraciones, en la misma, cuando apliquemos las propiedades algebraicas de los límites en cada uno de los términos correspondientes:
In order to simplify the demonstration, whose result is evident, let us make the following considerations, in the same, when we apply the algebraic properties of the limits in each of the corresponding terms:
1.-La función h es continua, entonces h(x+ Δx)=h(x), consecuentemente en cada denominador de la expresión anterior nos queda h2(x). //The function h is continuous, so h(x+ Δx)=h(x), consequently in each denominator of the above expression we are left with h2(x).
2.-
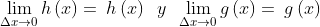.gif)
3.-
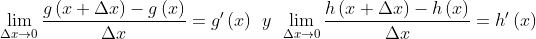.gif)
Por lo tanto: // Therefore:
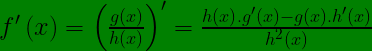.gif)
Lo cual corresponde a la regla que se utiliza para obtener la derivada de un cociente de funciones. // This corresponds to the rule used to obtain the derivative of a quotient of functions.
Aquí, en este post encontrará un ejemplo de aplicación. // Here, in this post you will find an example application.
https://hive.blog/math/@analealsuarez/the-derivative-of-a-quotient
