En post anteriores se estuvo estudiando los procedimientos que permiten obtener la derivada de una función, los mismos reciben el nombre de ``Técnicas de Derivación´´, y se resumen a continuación:
In previous posts we have been studying the procedures that allow us to obtain the derivative of a function, these are called ``Derivative Techniques'', and are summarized below:

Is important to highlight the importance of the concept of the derivative in terms of functions in different contexts, let's take the case of economics, in the field of economics, this concept is used to identify variables such as the speed of change in different phenomena such as, for example, the speed of change of the cost of production of a certain quantity of items, which is called "Marginal Cost", specifically, in this case it is the derivative of the cost function that is defined as Marginal Cost; Similarly, the derivative of the income function is defined as the Marginal income, and so it happens with all other functions in the economy.
Ejemplo/Example
A Company has determined that the function defining its revenue from the purchase and sale of its commodity x is R(x) = 2x + 4 x1/2 and therefore wishes to determine how fast its revenue changes in order to establish its profit criteria.
Solución:// Solution:
R'= (2x + 4 x1/2 )'=2-1/2(4x-1/2)=2- 2x-1/2
Este otro ejemplo lo dejamos al lector // This other example is left to the reader
El Costo de Producción de una mercancía es: C(x)= 2x - 6x +1, hallar el Costo Marginal.//The Cost of Production of a good is: C(x)= 2x - 6x +1, find the Marginal Cost.
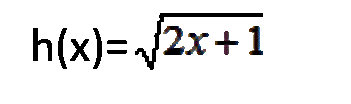
Nos preguntamos.//We wonder.
¿Se puede obtener la derivada de esta función con las fórmulas dadas en la tabla anterior? // Can the derivative of this function be obtained with the formulas given in the table above?
Vemos que no. // We see that we do not.
Vamos a conocer mejor a esta función H, considérese las funciones siguientes: // To learn more about this function H, consider the following functions:
f(x)= x1/2 y g(x)= 2x+1
¿Cómo se definiría f(g(x))? // How would f(g(x)) be defined?
Concluimos que la definición de esta función es H. // We conclude that the definition of this function is H.
Esta función recibe el nombre de Función Compuesta y se lee g compuesta con f.// This function is called Composite Function and is read g composed with f.
La función g se le denomina función Interna y f, función externa. Para obtener la derivada de esta función, se aplica una técnica, tal técnica se denomina la Regla de la Cadena la cual se define de la siguiente manera. // The function g is called internal function and f, external function. To obtain the derivative of this function, a technique is applied, this technique is called the Chain Rule which is defined as follows:
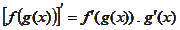
Encontrarás un ejemplo muy bien explicado en este post. // You will find a very well explained example in this post.
DERIVADA DE UN PRODUCTO COMBINADA CON REGLA DE LA CADENA
Espero que este post sea de utilidad, los invito a visitarme en mi blogspot personal. // I hope this post is useful, I invite you to visit me on my personal blogspot
https://analealsuarezvzla.blogspot.com/

.gif) , si la aplicamos a
, si la aplicamos a 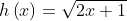.gif) . Asi:
. Asi: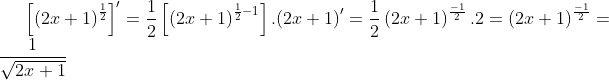.gif)