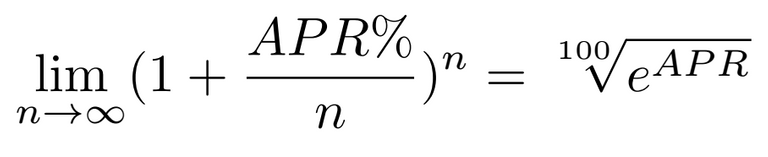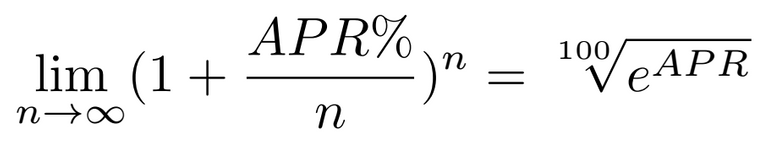
Beim jüngsten Engine-Stammtisch entbrannte eine heiße Diskussion zwischen @thatgermandude und mir. Aber was hat unsere Gemüter so erhitzt?
Einige in der Runde bezeichneten das Liquidity-Adden als Zinseszins. Ich haute ein entsetztes Veto in die Runde, diesem widersprachen @leosoph und @thatgermandude. Da kann ich nur sagen - gut so. Denn eine wichtige Regel der Mathematik lautet: Glaube erst mal nix und mach dir deine eigenen Gedanken.
Dies ist vermutlich auch eine gute Empfehlung für manch andere Belange im Leben. Aber ich möchte natürlich meine Gründe für das Veto näher ausführen. Viele von euch kennen bestimmt π. Die sogenannte Kreiszahl ist eine transzendente Zahl, welche ca. 3.41559... ist. In Dezimaldarstellung besitzt sie unendliche viele Nachkommastellen.
Nicht ganz so bekannt, aber genauso bedeutsam ist die eulersche Zahl e. e ist ca. 2.7182818284590452353602874713526624977572470936999595749669676277... (Anm. v. @quekery: ca.). Schülern kann man relativ einfach erklären, was π ist, auch wenn der Transzendenzbeweis eher nicht so Gegenstand einer schulischen Ausbildung ist. e taucht zwar auch in der Schule auf (i.d.R. in der 10. Klasse), aber wer kann sich schon daran erinnern?
Was bedeutet e denn nu?
Ich erkläre e gerne über den Jahreszins. Man könnte sich e wie einen unendlich feinen idealen Wachstumsfaktor vorstellen. Auch die e-Funktion hat unglaublich geniale Eigenschaften, aber das ist ein anderes Thema.
Die perfekte Verzinsung wirkt bestimmt auf viele Menschen wie etwas surreales. Etwas was kein echtes Äquivalent in der Realität findet. Ja, ein Klassiker der Mathematik könnte man meinen.
Aber dann kamen Liquidity-Pools. Pools ermöglichen sehr feinintervalliges nachpoolen. Wir könnten einmal im Monat (wie im Falle von HBD-Savings), einmal am Tag (Diesel-Pools) oder gar einmal pro Stunde (z.B. BSC oder ETH) etc. nachpoolen.
Und was würde eigentlich passieren, wenn wir unendlich "fein" nachpoolen wollen? BÄHM, hier kommt die eulersche Zahl ins Spiel. Wer hätte das gedacht, doch noch ne Anwendung in der Realität. Tatsächlich kommt sowas schon öfter vor in der Geschichte der Menschheit.
Naja, wir wollen uns mal nicht zu lange darüber freuen, dass Mathematik doch im Reallife ihre Anwendung findet. Zurück zur Mystik von e.
Wir stellen uns vor, wir haben einen Diesel-Pool mit einer APR von 100%. Fassen wir es mal als Jahreszins auf und vergessen kurz, dass es noch Gebühren gibt für das Nachpoolen und andere peakige Steine. Jetzt legen wir 1 USD für ein Jahr fest an. Nach einem Jahr hätten wir also 2 USD - nice. Ok, nur in unseren theoretischen Gedankenmodell, aber das ist doch auch was.
Jetzt könnten wir uns gemütlich zurücklegen und über die Verdoppelung freuen. Moment mal, würden wir nicht mehr bekommen, wenn wir unsere Zinsen monatlich nachpoolen? Dann testen wir dies doch gleich mal aus.
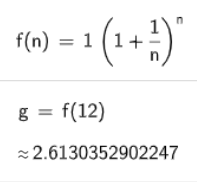
Ne Ver-2.6-fachung klingt doch schon mal besser als ne Verdopplung. Was wird wohl passieren, wenn wir täglich nachpoolen? Ne Vervierfachung, Verzehnfachung, Verdreißigfachung? Ist ja schließlich exponentiell und so. Wir bleiben gespannt:

Mh, was ging denn hier schief? Wollen wir mal stündlich nachpoolen. Wird es sich vervierfachen, verzehnfachen, verdreißigfachen?
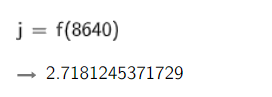
Mh, was ging denn hier schief? Wollen wir mal sekündlich nachpoolen. Wird eine Vervierfachung, Verzehnfachung, Verdreißigfachung stattfinden? Das war natürlich nur Spaß. Ich halte euch nicht mehr länger auf. Des Rätsels Lösung ist e. Würde man nanosekündlich oder pikosekündlich nachpoolen, würde man sich immer weiter e anähern, also 2.7182818284590452353602874713526624977572470936999595749669676277....
Endlich habe ich voll das Reallifebeispiel gefunden, um Leuten e näherzubringen und es ist nicht völlig aus den Fingern gesagt.
Und wenn wir ne andere APR haben?
Das ist eine ausgezeichnete Frage. Schauen wir uns kurz mal HBD an. Zum einfacheren Nachrechnen nehmen wir 10% statt 12%. Wir legen 100 HBD an und staken jährlich, monatlich, täglich bzw. stündlich nach:

Das ist jetzt aber nicht so viel Unterschied zum Jahreszins, bloß knapp 0.5 HBD, sagt ihr?
Aber @quekery nimm doch mal ne APR von 365 oder so. Ok, nehmen wir ne hohe.
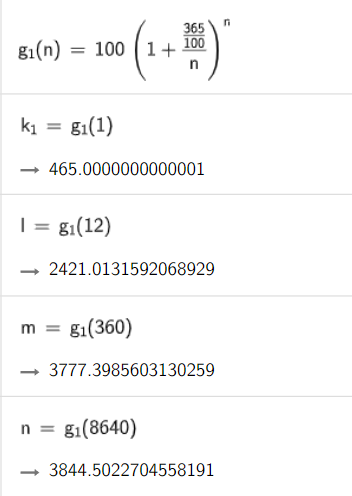
3844.5 ist jetzt aber schon deutlich mehr als 465? Ja ok, ihr habt mich, Das ist schon ein erheblicher Unterschied.
Das Resumé
Unser letztes Rechenbeispiel könnte man jetzt vielleicht mal visualisieren.
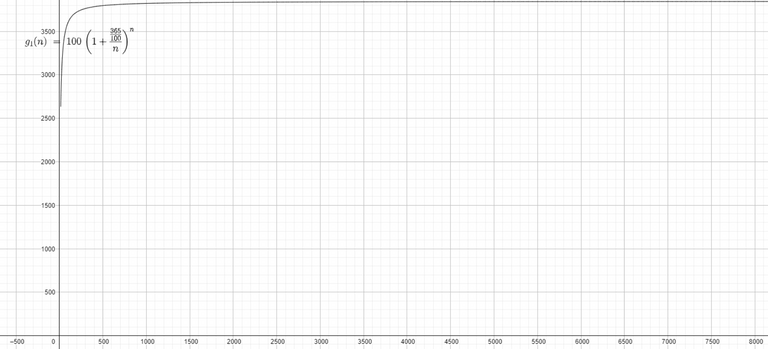
Wie wir sehen, bewegt sich unser Graph asymptotisch gegen einen bestimmten Wert, welcher btw. rund 3847.47 ist. Dies ist die 100te-Wurzel aus e hoch APR.
Posted using Dapplr