Square Root of Unity, Cube Root of Unity, and Complex Rotations

mes in #hive-128780 • 2 days ago

In this video I demonstrate that the square root of 1 (or unity) has two solutions while the cube root of unity has three solutions, two of which are rotations in the complex plane. I show this by first determining the factors using the difference of squares and cubes formulas. The difference of squares gives two factors or solutions: +1 and - 1. The difference of cubes gives the factor +1 and another factor in the form of a quadratic equation, which yields an additional 2 factors. Applying the quadratic formula and simplifying results in a square of a negative number, hence we obtain an imaginary number. This means yields 2 factors that are complex numbers, which I demonstrate are just rotations of 120° and 240° counterclockwise in the complex plane. These solutions will be required for obtaining the solutions of the cubic formula!

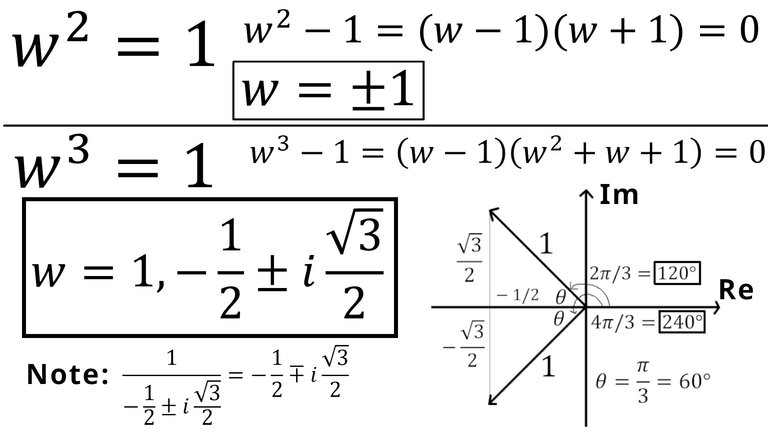
5 Cube Root of Unity.jpeg

Timestamps

Cube root gives 3 solutions just as square root gives 2 solutions: 0:00
Difference of squares for square root of unity gives 2 solutions: 1:07
Difference of cubes for square root of unity gives 3 solutions: 3:11
2nd cube root has 2 solutions via the PQ quadratic equation: 5:15
2nd cube root solutions are complex or involve imaginary numbers: 7:01
Note that the complex solutions are inversely equal to each other: 8:30
The complex factors are just rotations in the complex plane: 11:40
Solving complex angles via exact trigonometric ratios: 14:16
Complex angles are 120 degrees and 240 degrees: 15:47
Summary of cube roots of unity: 1, complex rotation of 120°, complex rotation of 240°: 16:44

Notes and Playlist

Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0EF05ExjzLbB64NgUjoV1hl
Notes: https://peakd.com/hive-128780/@mes/dzekfnxh .

Become a MES Super Fan! https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join

DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate

SUBSCRIBE via EMAIL: https://mes.fm/subscribe

MES Links: https://mes.fm/links

MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes

Email me: contact@mes.fm

Free Calculators: https://mes.fm/calculators

BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm

Free Online Tools: https://mes.fm/tools

iPhone and Android Apps: https://mes.fm/mobile-apps

▶️ 3Speak

#math #science #education #algebra #stemgeeks #chessbrothers #stem #palnet #proofofbrain #mathematics

Sort:

Trending

[-]

mes 2 days ago

!summarize

0.04 VYB

1 vote

[-]

ai-summaries 2 days ago

Part 4/5:

An intriguing relationship exists between these roots: the reciprocal of one will yield another. For example, by taking the reciprocal of (z_1):

[

\frac{1}{z_1} = \frac{2}{-1 + i\sqrt{3}}

]

By multiplying the numerator and denominator by the conjugate, one can simplify this expression to reveal its connection to (z_2), demonstrating that every root has a mathematical relation with others.

Conclusion

The cube roots of unity embody a rich tapestry of algebra and geometry. By dissecting the polynomial equation and leveraging the quadratic formula, we reveal the hidden structure of these roots within the complex plane. Not only do we acquire solutions but also gain an understanding of how they interact and represent rotations—a beautiful interplay between arithmetic and geometry.

0.00 VYB

[-]

ai-summaries 2 days ago

Part 1/5:

Understanding the Cube Root of Unity

In this exploration, we delve into a fundamental concept in algebra related to the roots of unity, specifically focusing on the cube root of unity. This discussion not only sheds light on the derivation of these roots but also provides insight into complex numbers and their geometric interpretations.

The Nature of Cube Roots

When calculating the cube root of a number, one anticipates multiple solutions, specifically three for any non-zero complex number. This contrasts with square roots, which yield two solutions. To illustrate this, consider the equation (z^3 = 1). Here, we want to extract the values of (z) that satisfy the equation.

Factorization: Roots of Unity

0.00 VYB

[-]

ai-summaries 2 days ago

Part 3/5:

( z_1 = \frac{-1 + i\sqrt{3}}{2} )
( z_2 = \frac{-1 - i\sqrt{3}}{2} )

Complex Solutions and Their Geometric Interpretation

The two complex solutions are represented in the complex plane. It is important to understand that these solutions signify rotations. The term "imaginary" may evoke confusion but can be interpreted as indicating direction.

The solutions can be seen as rotations around the origin in the complex plane. The angle corresponding to (z_1) is (120^\circ) or (\frac{2\pi}{3}) radians, while (z_2) rests at (240^\circ) or (\frac{4\pi}{3}) radians. This geometrical perspective underlines the significance of complex numbers as not just quantities but as vectors that exist in two dimensions.

Relationship Among the Roots

0.00 VYB

[-]

ai-summaries 2 days ago

Part 5/5:

Through this journey, we appreciate the elegance of mathematical concepts, illuminating the path between abstract numbers and their geometric representations.

0.00 VYB

[-]

chessbrotherspro 2 days ago

Congratulations!

✅ Good job. Your post has been appreciated and has received support from CHESS BROTHERS ♔ 💪

♟ We invite you to use our hashtag #chessbrothers and learn more about us.

♟♟ You can also reach us on our Discord server and promote your posts there.

♟♟♟ Consider joining our curation trail so we work as a team and you get rewards automatically.

♞♟ Check out our @chessbrotherspro account to learn about the curation process carried out daily by our team.

🏅 If you want to earn profits with your HP delegation and support our project, we invite you to join the Master Investor plan. Here you can learn how to do it.

Kindly

The CHESS BROTHERS team

0.00 VYB