~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
04-11-2024 - Analytic Geometry - Matrix Multiplication Example [EN]-[IT]
With this post I would like to give a brief instruction regarding the topic mentioned in the subject
(code notes: X_086)
Matrix Multiplication Example
Let's proceed with the multiplication between the following matrices
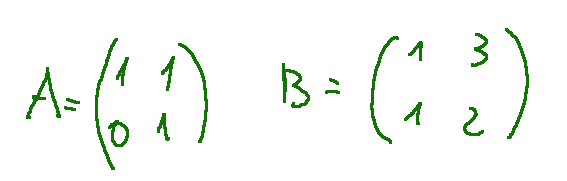
The result for us will be the matrix C which will have the following terms as result
c11=a11⋅b11+a12⋅b21
c12=a11⋅b12+a12⋅b22
c21=a21⋅b11+a22⋅b21
c22=a21⋅b12+a22⋅b22
Let's replace the terms
c11=1⋅1+1⋅2
c12=1⋅3+1⋅2
c21=0⋅1+1⋅1
c22=0⋅3+1⋅2
We will obtain the following results
c11=1⋅1+1⋅2 = 1 + 2 = 3
c12=1⋅3+1⋅2 = 3 + 2 = 5
c21=0⋅1+1⋅1 = 0 + 1 = 1
c22=0⋅3+1⋅2 = 0 + 2 = 2
So the resulting matrix will be the following
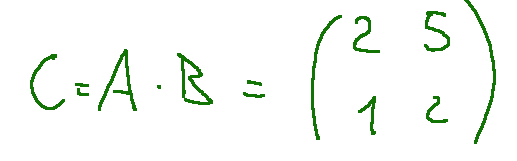
Inverse matrix
Let's try to find the inverse matrix of
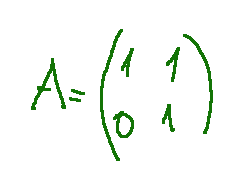
Consider the following system
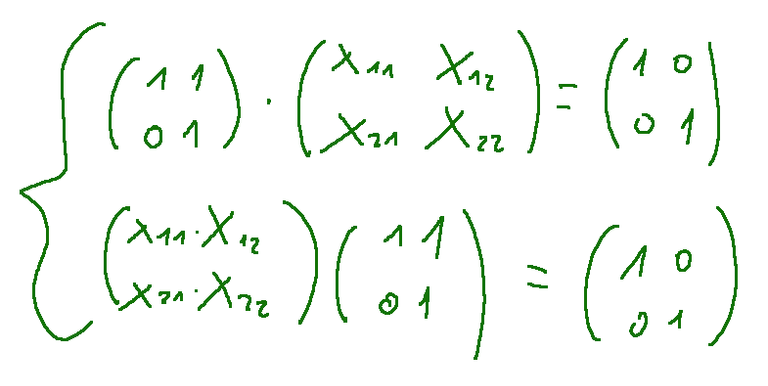
The unknown is a matrix. Now let's do the two products row by column.
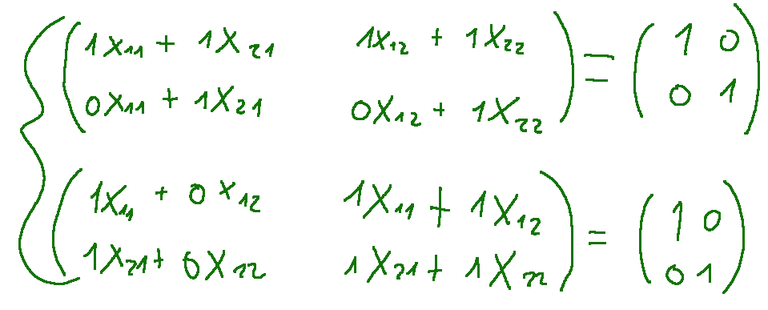
At this point we have a system of 8 equations
1 x11 + 1 x21 = 1
1 x12 + 1 x22 = 0
0 x11 + 1 x21 = 0
0 x12 + 1 x22 = 1
1 x11 + 0 x12 = 1
1 x11 + 1 x12 = 0
1 x21 + 0 x22 = 0
1 x21 + 1 x22 = 1
For solution has the quaterna (x11,x12,x21,x22) = (1, -1, 0, 1)
Let's do two checks with the first two rows and the last one
1 x11 + 1 x21 = 1 ---> 1 x 1 + 1 x 0 = 1
1 x12 + 1 x22 = 0 ---> 1 x -1 + 1 x 1 = 0
…
1 x21 + 1 x22 = 1 ---> 1 x 0 + 1 x 1 = 1
Conclusions
Matrix multiplications are obtained by multiplying the rows with the columns.
Question
In my opinion matrix multiplications are not an easy thing to understand, what do you think?

[ITALIAN]
04-11-2024 - Geometria analitica - Esempio moltiplicazione di matrici [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_086)
Esempio moltiplicazione di matrici
Procediamo con la moltiplicazione tra le seguenti matrici
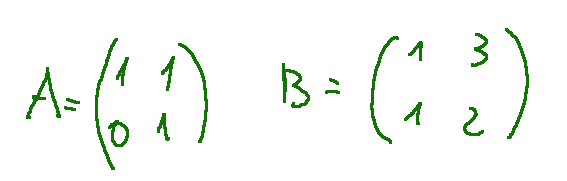
Il risultato per noi sarà la matrice C che avrà i seguenti termini come risultato
c11=a11⋅b11+a12⋅b21
c12=a11⋅b12+a12⋅b22
c21=a21⋅b11+a22⋅b21
c22=a21⋅b12+a22⋅b22
Andiamo a sostituire i termini
c11=1⋅1+1⋅2
c12=1⋅3+1⋅2
c21=0⋅1+1⋅1
c22=0⋅3+1⋅2
Otterremo i seguenti risultati
c11=1⋅1+1⋅2 = 1 + 2 = 3
c12=1⋅3+1⋅2 = 3 + 2 = 5
c21=0⋅1+1⋅1 = 0 + 1 = 1
c22=0⋅3+1⋅2 = 0 + 2 = 2
Quindi la matrice risultante sarà la seguente
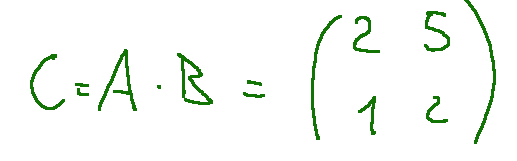
Matrice inversa
Proviamo a trovare la matrice inversa di
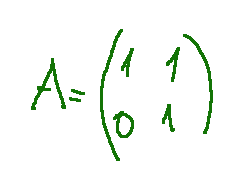
Consideriamo il seguente sistema
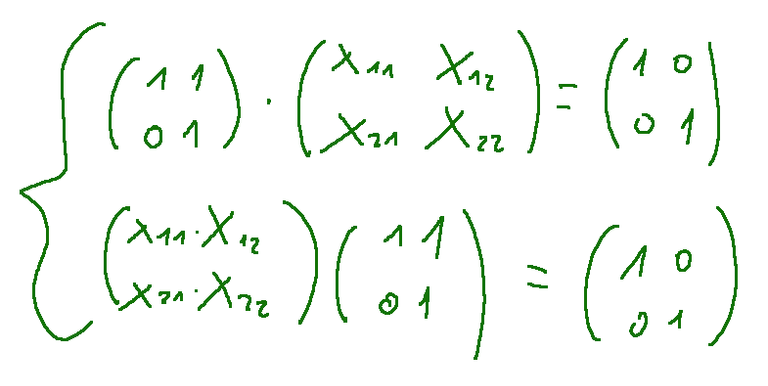
L’incognita è una matrice. Ora facciamo i due prodotti righe per colonne.
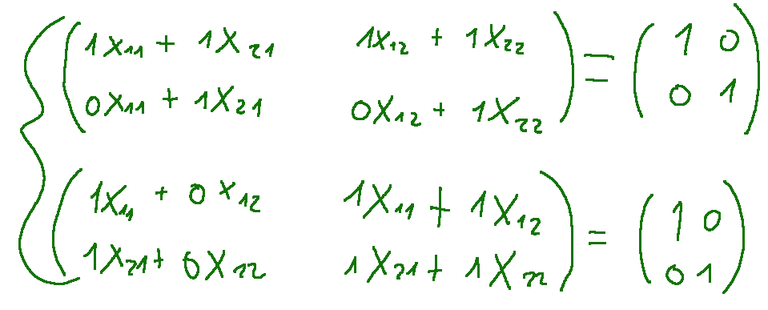
A questo punto abbiamo un sistema di 8 equazioni
1 x11 + 1 x21 = 1
1 x12 + 1 x22 = 0
0 x11 + 1 x21 = 0
0 x12 + 1 x22 = 1
1 x11 + 0 x12 = 1
1 x11 + 1 x12 = 0
1 x21 + 0 x22 = 0
1 x21 + 1 x22 = 1
Per soluzione ha la quaterna (x11,x12,x21,x22) = (1, -1, 0, 1)
Facciamo due verifiche con le prime due righe e l’ultima
1 x11 + 1 x21 = 1 ---> 1 x 1 + 1 x 0 = 1
1 x12 + 1 x22 = 0 ---> 1 x -1 + 1 x 1 = 0
…
1 x21 + 1 x22 = 1 ---> 1 x 0 + 1 x 1 = 1
Conclusioni
Le moltiplicazioni con le matrici si ottengono moltiplicando le righe con le colonne.
Domanda
Secondo me le moltiplicazioni tra matrici non sono una cosa facile da comprendere, voi che ne pensate?
THE END

