
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
05-11-2024 - Analytic Geometry - Determinant of 3x3 matrix [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_085)
Determinant of 3x3 matrix
The determinant of a matrix is a number associated with each square matrix, and expresses some of its algebraic and geometric properties.
In this article I will show the steps that need to be done to calculate the determinant of a 3x3 matrix.
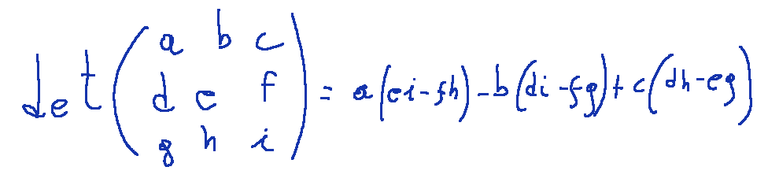
Let's now take the following matrix as an example
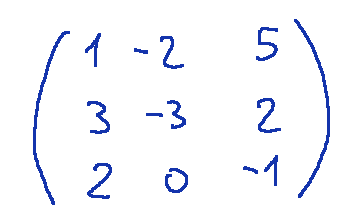
We will therefore have that the determinant will be
a(ei−fh)−b(di−fg)+c(dh−eg)
so thinking about the given matrix
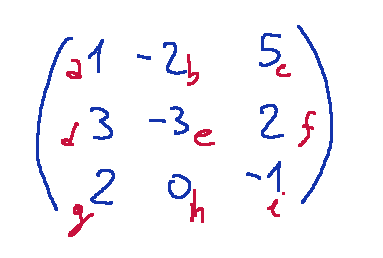
we can perform the calculation thinking in two ways
1- det = a(ei−fh)−b(di−fg)+c(dh−eg)
2- det = a11a22a33 - a11a23a32 + a12a23a31 - a12a21a33 + a13a21a32 - a13a22a31
The result is 19
Conclusions
To calculate the determinant of a 3x3 matrix, you need to multiply each element of the first row by the determinant of the 2×2 matrix obtained by eliminating the row and column of the element.
Question
Have you ever tried to calculate the determinant of a 3 x 3 matrix?

[ITALIAN]
05-11-2024 - Geometria analitica - Determinante matrice 3x3 [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_085)
Determinante matrice 3x3
Il determinante di una matrice è un numero associato a ciascuna matrice quadrata, e ne esprime alcune proprietà algebriche e geometriche.
In questo articolo mostrerò i passi che bisogna fare per calcolare il determinante di una matrice 3x3.
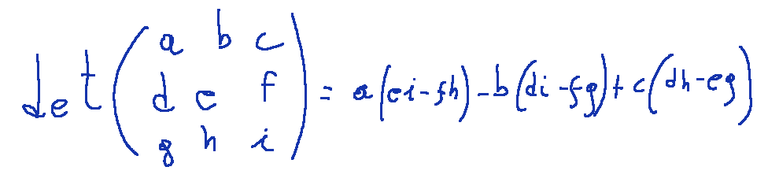
Prendiamo ora come esempio la seguente matrice
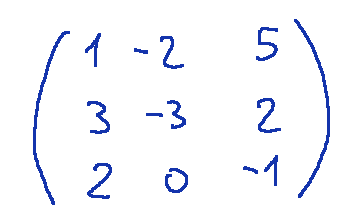
Avremo quindi che il determinante sarà
a(ei−fh)−b(di−fg)+c(dh−eg)
quindi pensando all amatrice data
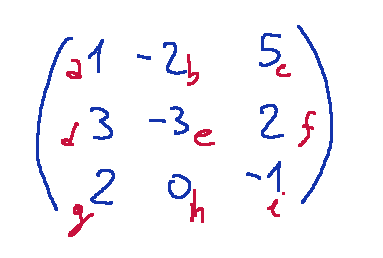
possiamo effettuare il calcolo pensado in due maniere
1- det = a(ei−fh)−b(di−fg)+c(dh−eg)
2- det = a11a22a33 - a11a23a32 + a12a23a31 - a12a21a33 + a13a21a32 - a13a22a31
Il risultato è 19
Conclusioni
Per calcolare il determinante di una matrice 3x3 bisogna moltiplicare ciascun elemento della prima riga per il determinante della matrice 2×2 ottenuta eliminando la riga e la colonna dell’elemento.
Domanda
Avete mai provato a calcolare il determinante di una matrice 3 x 3?
THE END



