
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
14-11-2024 - Analytic Geometry - Changes of Basis [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_77)
Changes of Basis
The coordinates of a vector change if the basis changes.
The change of basis allows to reinterpret the coordinates of the vectors and the linear expressions with respect to different bases, sometimes simplifying the calculations or revealing hidden properties of linear transformations.
The key concepts are the following:
-Basis. A basis in a vector space V is a set of linearly independent vectors that generate V. Every vector in the space can be represented as a linear combination of the vectors of the basis.
-Coordinates. The coordinates of a vector with respect to a basis are the coefficients that are used to express that vector as a linear combination of the basis vectors.
Below is an example.
If…
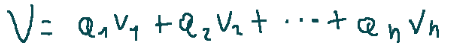
then the coordinates of v with respect to this basis are…
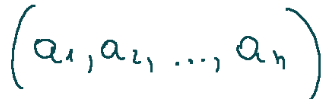
-Change of basis matrix
Given a vector space V and two bases
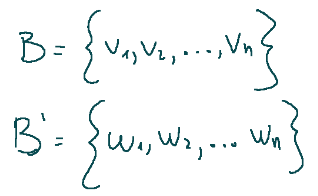
the basis change matrix P from B to B’ is a matrix that allows you to transform the coordinates of a vector from one basis to another.
-Calculating the basis change matrix.
To find the basis change matrix P from B to B’, the vectors of the basis B are expressed as a linear combination of the vectors of B’.
The coordinates of each vector of B with respect to the vectors of B’ form the columns of P.
What are basis changes used for
-Simplifying linear transformations
-Revealing geometric properties
-Normalizing calculations
Example
Let B, B’ and B’’ be bases of a finitely generated vector space V such that the basis change matrices are the two expressed below.
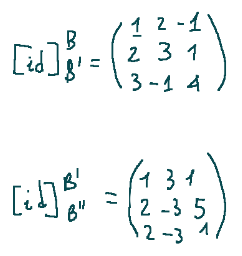
Now let's try to calculate the change of basis matrix
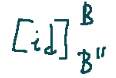
Process
We have that the composition of the identity function idv is the identity function idv, so we have continued…
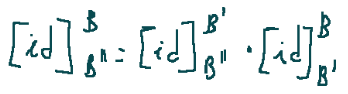
The basis change matrix is
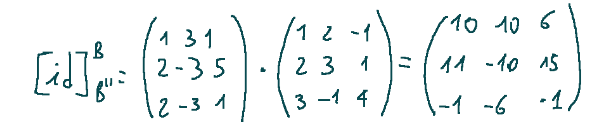
Conclusions
The basis change is a process that is used to go from one basis to another in the vector space. It is mainly used to simplify linear transformations and detect geometric properties.
Question
Have you ever heard of a change of basis in vector space? Have you covered these topics in analytical geometry?

[ITALIAN]
14-11-2024 - Geometria analitica - Cambiamenti di base [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_77)
Cambiamenti di base
Le coordinate di un vettore cambiano se cambia la base.
Il cambiamento di base permette di reinterpretare le coordinate dei vettori e le espressioni lineari rispetto a diverse basi, semplificando a volte i calcoli o rivelando proprietà nascoste delle trasformazioni lineari.
I concetti chiave sono i seguenti:
-Base. Una base in uno spazio vettoriale V è un insieme di vettori linearmente indipendenti che generano V. Ogni vettore nello spazio può essere rappresentato come combinazione lineare dei vettori della base.
-Coordinate. Le coordinate di un vettore rispetto a una base sono i coefficienti che servono per esprimere quel vettore come combinazione lineare dei vettori base.
Qui di seguito un esempio.
Se…
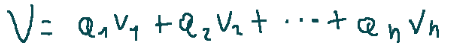
allora le coordinate di v rispetto a questa base sono…
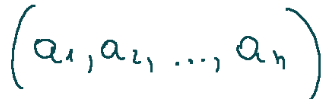
-Matrice cambiamento di base
Dato uno spazio vettoriale V e due basi
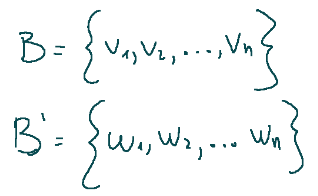
la matrice di cambiamento di base P da B a B’ è una matrice che permette di trasformare le coordinate di un vettore da una base all’altra.
-Calcolo della matrice di cambiamento di base.
Per trovare la matrice di cambiamento di base P da B a B’, si esprimono i vettori della base B come combinazione lineare dei vettori di B’.
Le coordinate di ogni vettore di B rispetto ai vettori di B’ formano le colonne di P.
A cosa servono i cambiamenti di base
-Semplificare le trasformazioni lineari
-Rivelare proprietà geometriche
-Normalizzare i calcoli
Esempio
Siano B, B’ e B’’ basi di uno spazio vettoriale finitamente generato V tali che le matrici di cambiamento di base siano le due espresse qui di seguito.
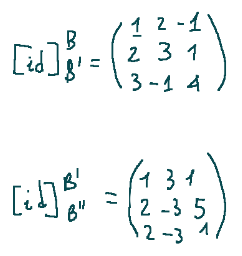
Proviamo ora a calcolare la matrice di cambiamento di base
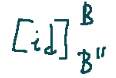
Svolgimento
Abbiamo che la composizione della funzione identità idv è la funzione identità idv, quindi abbiamo quanto segue…
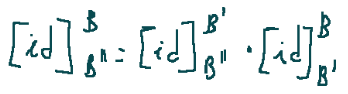
La matrice di cambiamento di base è
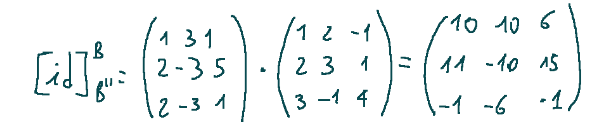
Conclusioni
Il cambiamento di base è un processo che viene usato per passare da una base a un’altra nello spazio vettoriale. Si usa principalmente per semplificare le trasformazioni lineari e rilevare proprietà geometriche.
Domanda
Avete mai sentito parlare di un cambio di base nello spazio vettoriale? Avete affrontato questi argomenti in geometria analitica?
THE END






