
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
16-11-2024 - Analytic Geometry - Systems of Linear Equations [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_76)
Systems of Linear Equations
Matrices and linear applications can be combined to study systems of linear equations
Below is shown a system of linear equations with 2 equations and 2 unknowns. This system is linear and real.
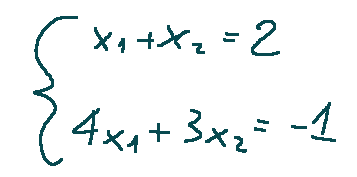
We can also say that a system of linear equations is a set of equations in which each equation is linear and which takes the following form.
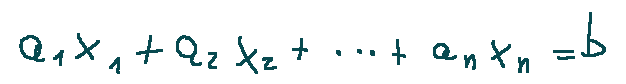
Where:
a1, a2,...,an are the coefficients of the variables x1, x2,...,xn
b is the known term
n is the number of variables
The purpose of linear equations is to find the values of the variables x1,x2,...,xn that satisfy the system of equations.
Example
Let's consider the following system:
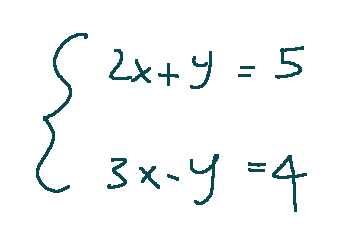
The first step we can take is to isolate the y:
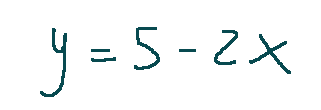
Now let's substitute the second expression y
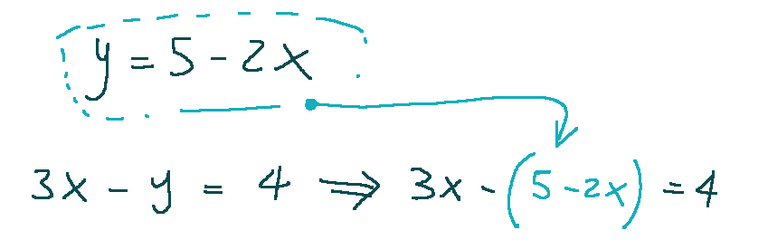
Continuing with the calculations we will have that…
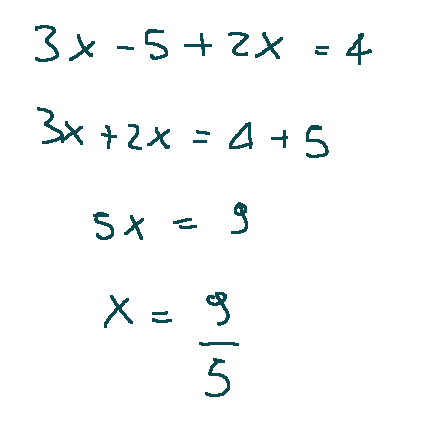
Now let's calculate y
Let's go back to the first equation and replace x with the value we just found, that is 9/5.
We will get the following:
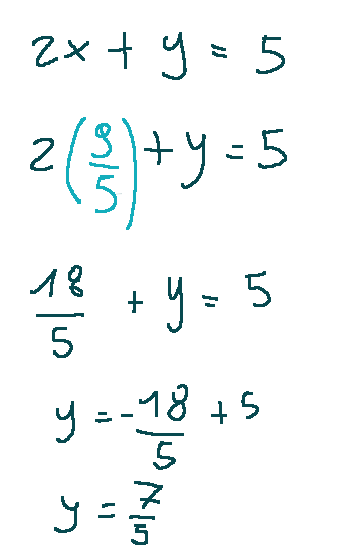
Result
So the final result will be:
X = 9/5, y = 7/5
Matrix representation
We can write the equation described above in matrix form and it turns out as follows:
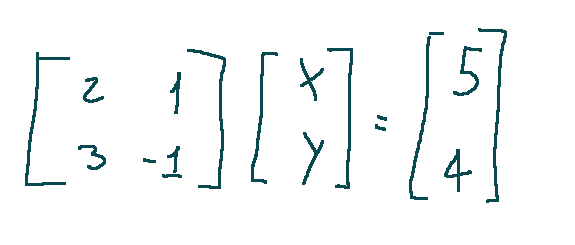
Where:
Matrix A contains the coefficients
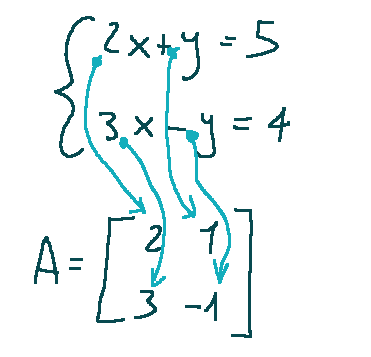
Vector X contains the unknowns
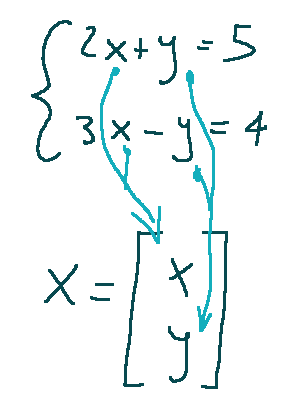
Vector B contains the known terms
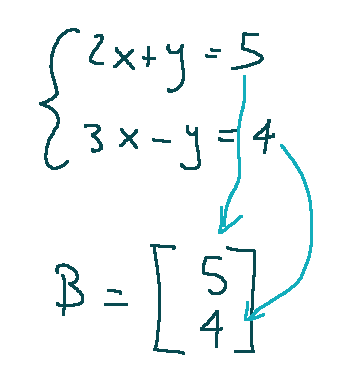
Conclusions
_To solve the linear equation of matrices we can use the Gaussian elimination method or other techniques matrix.
Question
Linear equations between matrices are a not very common topic, did you study them at school?

[ITALIAN]
16-11-2024 - Geometria analitica - Sistemi di equazioni lineari [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_76)
Sistemi di equazioni lineari
Le matrici e le applicazioni lineari possono essere combinati per studiare i sistemi di equazioni lineari
Qui di seguito è mostrato un sistema di equazioni lineari con 2 equazioni e 2 incognite. Questo sistema è lineare e reale.
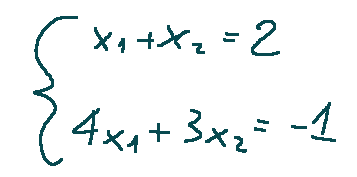
Possiamo dire anche che un sistema di equazioni lineari è un insieme di equazioni in cui ogni equazione è lineare e che assume la seguente forma.
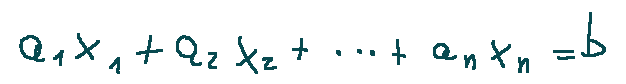
Dove:
a1, a2,...,an sono i coefficienti delle variabili x1, x2,...,xn
b è il termine noto
n è il numero di variabili
Lo scopo delle equazioni lineari è trovare i valori delle variabili x1,x2,...,xn che soddisfano il sistema di equazioni.
Esempio
Consideriamo il sistema seguente:
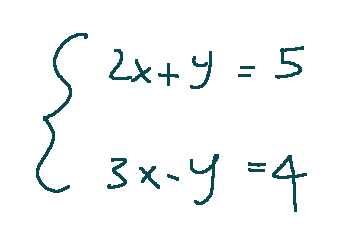
Il primo passo che possiamo fare è isolare la y:
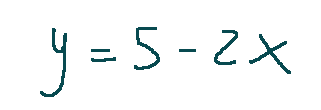
Passiamo ora a sostituire nella seconda espressione la y
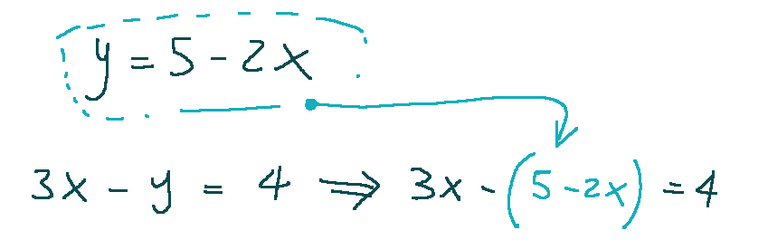
Continuando con i calcoli avremo che…
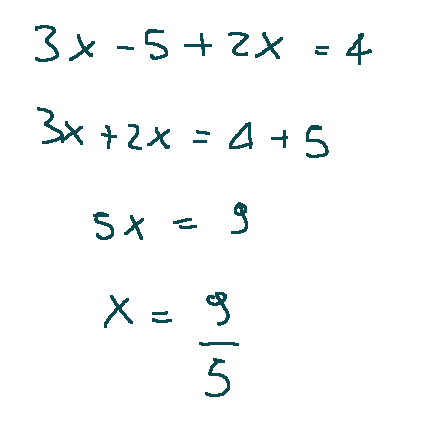
Ora passiamo a calcolare y
Riprendiamo la prima equazione e sostituiamo la x con il valore che abbiamo appena trovato, cioè 9/5.
Otterremo quanto segue:
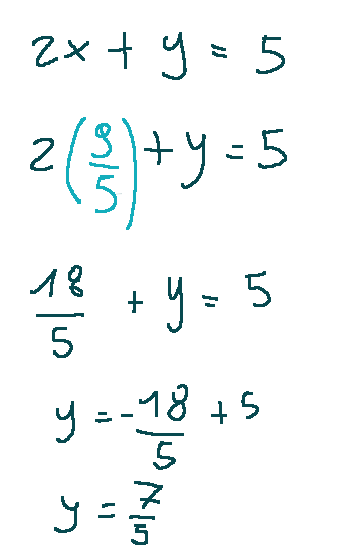
Risultato
Quindi il risultato finale sarà:
X = 9/5, y = 7/5
Rappresentazione con matrice
Possiamo scrivere l’equazione prima descritta in forma di matrice e risulta come segue:
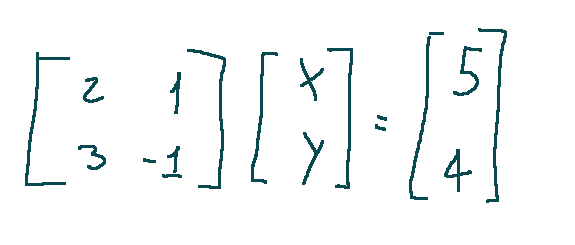
Dove:
La matrice A contiene i coefficienti
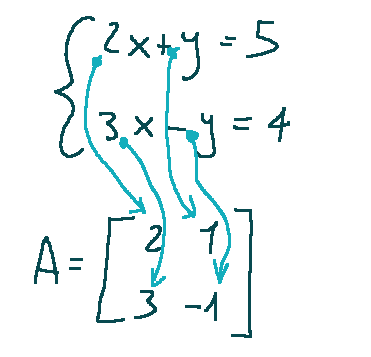
il vettore X contiene le incognite
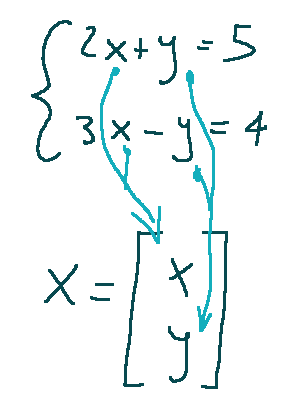
Il vettore B contiene i termini noti
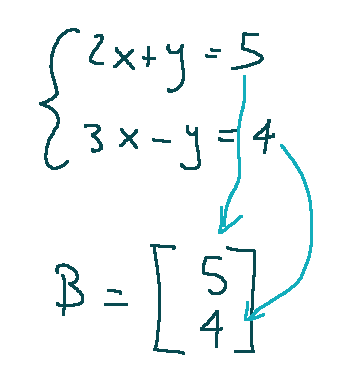
Conclusioni
_Per risolvere l’equazione lineare delle matrici possiamo usare il metodo di eliminazione di Gauss o altre tecniche matriciali.
Domanda
L'equazioni lineari tra matrici è un argomento poco diffuso, le avete studiate a scuola?
THE END



