
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
21-11-2024 - Analytic Geometry - Diagonalization [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_72)
Diagonalization
Description
Studying the diagonalization of endomorphisms means seeing when they have enough eigenvectors to form a basis.
Let's remember the concept of endomorphism.
In linear algebra, an endomorphism is a particular case of a morphism of vector spaces, that is, a linear application that maps a vector space V into itself.
Formally, an endoformism is a function
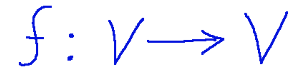
that satisfies the linearity properties:
1-Additivity.
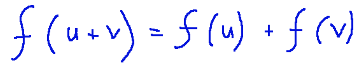
for everyone

2-Compatibility with scalar multiplication.
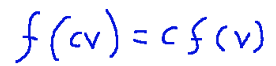
Example
Find the diagonal joint matrix and a corresponding diagonalizing matrix of the following matrix.
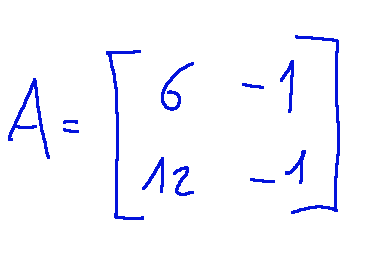
-Step 01
First we calculate the eigenvalues λ by solving the characteristic equation:
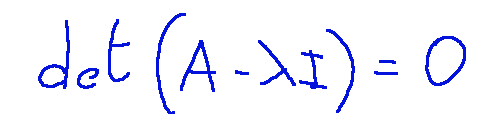
In this case I is the identity matrix. YES it is calculated:
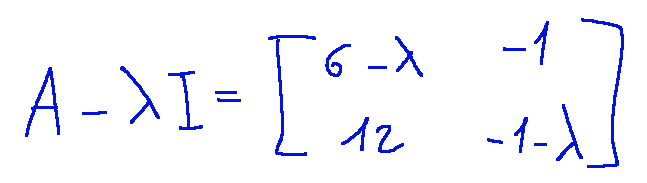
The determinant will be as follows
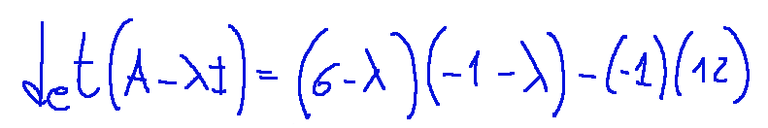
proceeding with the calculations we arrive at the following result
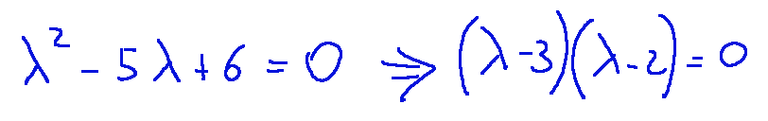
So the eigenvalues are:
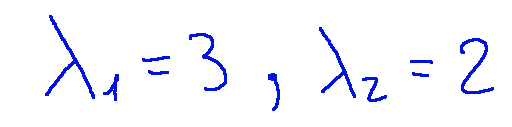
-Step 02: the eigenvectors
For each eigenvalue λ, we calculate the eigenvectors by solving the following expression
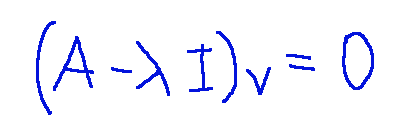
For λ1 = 3 an associated eigenvector is
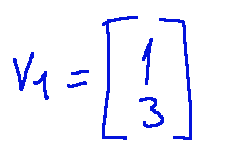
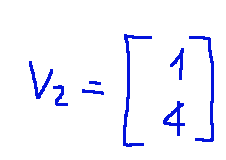
-Step 03: Construction of P and D
The diagonalizing matrix P has the eigenvectors as columns while D has the eigenvalues on the diagonal. Here is their construction.
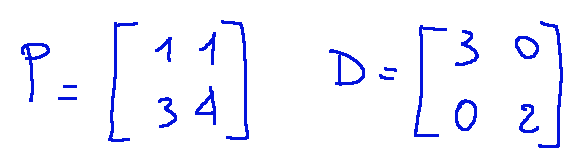
Result
The joint diagonal matrix is:
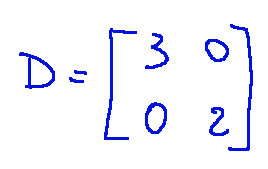
The diagonalizing matrix is:
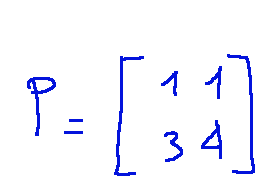
Conclusions
Knowing the joint diagonal matrix and the diagonalizing matrix is fundamental in linear algebra because it greatly facilitates the calculation and interpretation of matrix operations, in particular for square matrices that represent linear transformations
Question
Identifying the joint diagonal matrix and the diagonalizing matrix is an activity that I understood only after a lot of practice, is this an easy or difficult topic for you?

[ITALIAN]
21-11-2024 - Geometria analitica - Diagonalizzazione [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_72)
Diagonalizzazione
Descrizione
Studiare la diagonalizzazione degli endoformismo significa vedere quando essi hanno abbastanza autovettori per formare una base.
Ricordiamo il concetto di endomorfismo.
In algebra lineare, un endoformismo è un caso particolare di morfismo di spazi vettoriali, ovvero una applicazione lineare che mappa uno spazio vettoriale V in sé stesso.
Formalmente, un endoformismo è una funzione
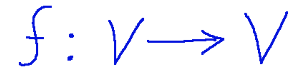
che soddisfa le proprietà di linearità:
1-Additività.
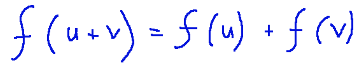
per tutti

2-Compatibilità con la moltiplicazione scalare.
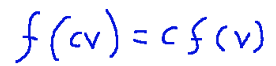
Esempio
Trovare la matrice congiunta diagonale e una matrice diagonalizzante corrispondente della seguente matrice.
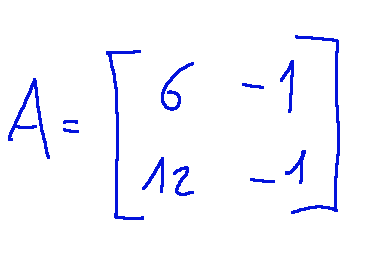
-Passo 01
Per prima cosa calcoliamo gli autovalori λ risolvendo l’equazione caratteristica:
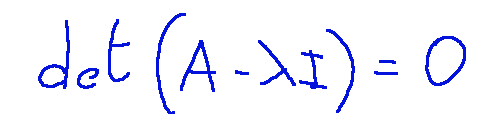
In questo caso I è la matrice identità. SI calcola:
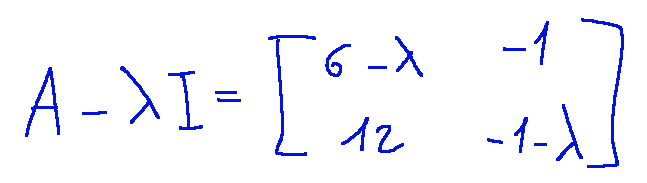
Il determinante risulterà come segue
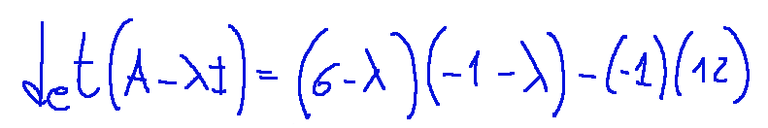
procedendo con i calcoli arriviamo al seguente risultato
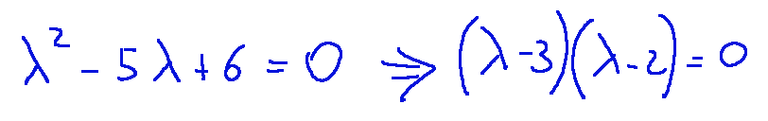
Quindi gli autovalori sono:
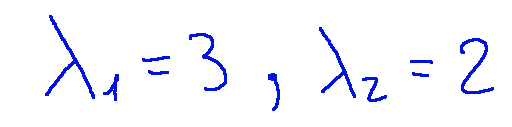
-Passo 02: gli autovettori
Per ciascun autovalore λ, calcoliamo gli autovettori risolvendo la seguente espressione
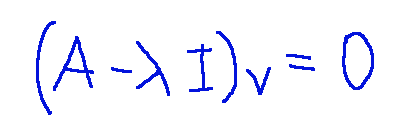
Per λ1 = 3 un autovettore associato è
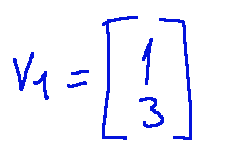
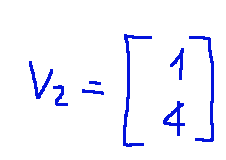
-Passo 03: Costruzione di P e D
La matrice diagonalizzante P ha come colonne gli autovettori mentre D ha gli autovalori sulla diagonale. Qui di seguito la loro costruzione.
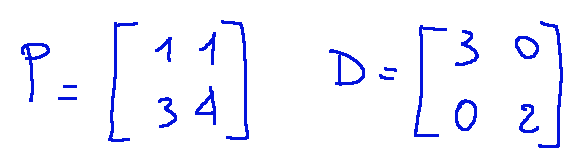
Risultato
La matrice diagonale congiunta è:
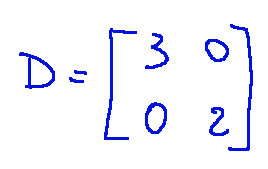
La matrice diagonalizzante è:
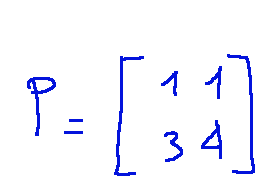
Conclusioni
Sapere la matrice diagonale congiunta e la matrice diagonalizzante è fondamentale in algebra lineare perché facilita notevolmente il calcolo e l'interpretazione delle operazioni su matrici, in particolare per matrici quadrate che rappresentano trasformazioni lineari
Domanda
Individuare la matrice diagonale congiunta e la matrice diagonalizzante è un attività che ho compreso solo dopo molto esercizio, per voi questo è un argomento facile o difficile?
THE END