
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
22-10-2024 - Analytic geometry - coordinates and vector [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_091)
coordinates and vector
In this article I will give an example of how to find the coordinates of a vector, but be careful, I will not explain some basic concepts, perhaps without these basic concepts the expressions shown could be incomprehensible.
Exercise
Let's find the coordinates and the vector of the coordinates of the following vectors with respect to the basis of the respective vector space.
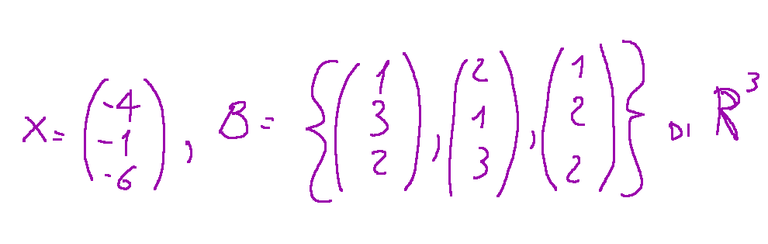
What we need to do now is find the coefficients c1, c2 and c3 that can generate the vector X = (-4 -1 -6) (written as a row vector)
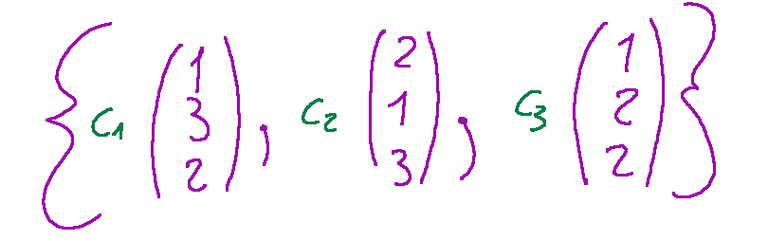
Let's remember our column vector X which is the following
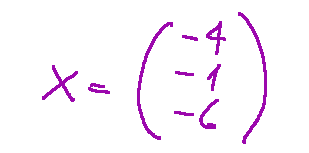
What we need to do now is find the right coefficient for c1, c2 and c3 that multiplied by the upper numbers of the column vectors and added together gives a result of -4
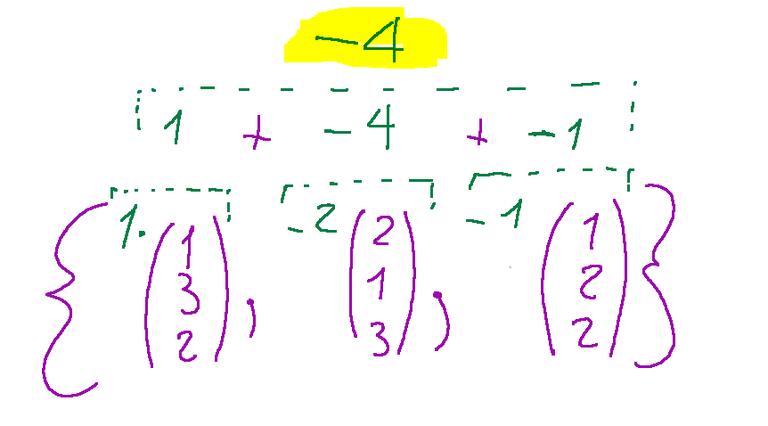
So c1=1, c2=-4 and c3=-1
Now let's check that these coefficients are able to generate the entire vector X that we were given and note that this condition is verified.
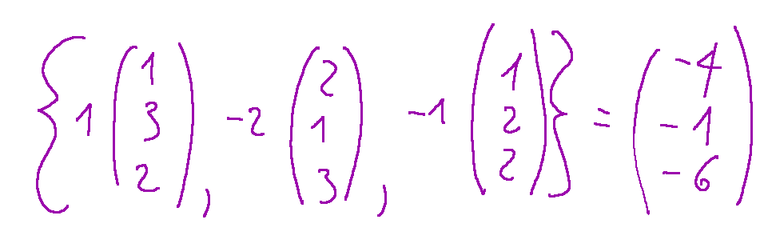
So we will have that the coordinates and the vector of the coordinates of the given vectors with respect to the basis of the respective vector spaces are the following.
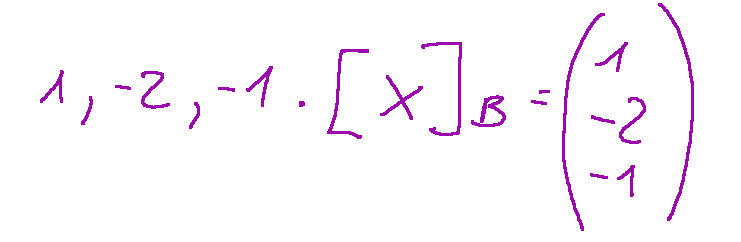
Conclusions
The coefficients of column vectors are fundamental elements for the generation of vectors of a given set.
Question
Have you ever done similar exercises?

[ITALIAN]
22-10-2024 - Geometria analitica - le coordinate ed il vettore [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_091)
le coordinate ed il vettore
In questo articolo farò un esempio di come trovare le coordinate di un vettore, ma attenzione, non spiegherò alcuni concetti base, forse senza questi concetti base le espressioni mostrate potrebbero risultare incomprensibili.
Esercizio
Troviamo le coordinate ed il vettore delle coordinate dei vettori seguenti rispetto alla base del rispettivo spazio vettoriale.
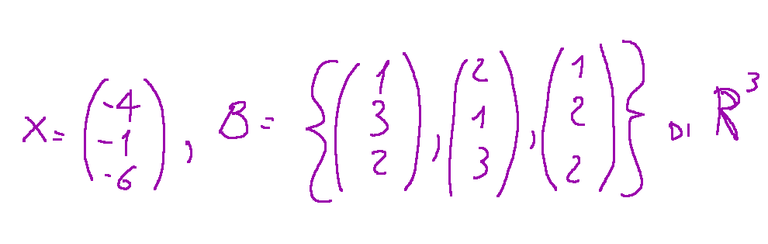
Quello che dobbiamo fare è ora trovare i coefficienti c1, c2 e c3 che possono generare il vettore X = (-4 -1 -6) (scritto sotto forma di vettore riga)
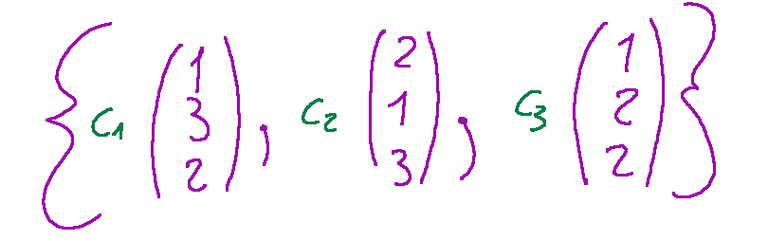
Ricordiamo il nostro vettore colonna X che è il seguente
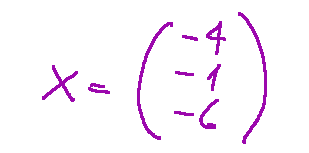
Quello che dobbiamo fare ora è trovare il coefficiente giusto per c1, c2 e c3 che moltiplicati ai numeri superiori dei vettori colonna e sommati dia un risultato di -4
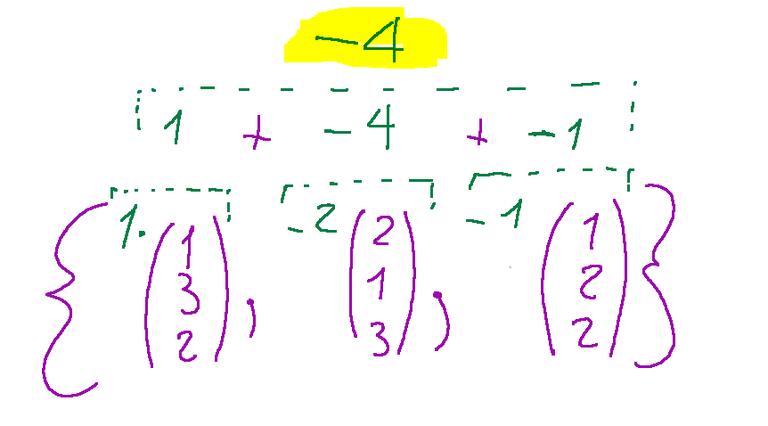
Quindi c1=1, c2=-4 e c3=-1
Ora verifichiamo che questi coefficienti siano in grado di generare tutto il vettore X che ci è stato dato e notiamo che questa condizione è verificata.
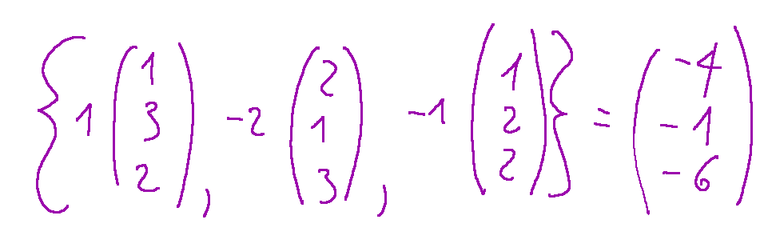
Quindi avremo che le coordinate e il vettore delle coordinate dei vettori dati rispetto alla base dei rispettivi spazi vettoriali sono i seguenti.
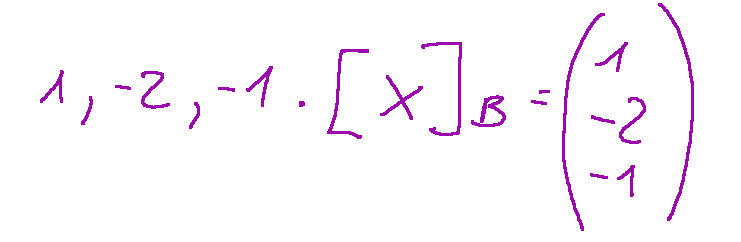
Conclusioni
I coefficienti dei vettori colonna sono elementi fondamentali per la generazione dei vettori di un determinato insieme.
Domanda
Avete mai eseguito esercizi simili?
THE END



