
Introduction
Many mathematical proofs are based on deductive reasoning. One fact leads to another and like a detective solving a crime the mathematician takes what is known (so called axioms and premises) and comes to a logical conclusion that proves the theorem.
But every once in a while (and more often than one might think) this kind of thinking is combined with a kind of proof called Mathematical Induction. And the best way to describe it is: The Domino Effect.
Example
Little Gauß at school
You probably heard of the German mathematician Carl Friedrich Gauß (1777-1855). If not, no worries.
When he was nine years old, his math teacher gave the class the task to sum up all (whole) numbers from 1 to 100. Within a few minutes Gauß had the answer as 5050 and was done while all other students where still adding and scribbling. How did he do it?
Gauß realized there was a simple formula to perform this task.
Whenever you need to sum up the numbers from 1 to X you do the following: Multiply X with its successor and divide the result by 2.
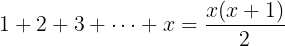
But does it really work all the time? Or was it just pure luck?
We could simply plug in a few numbers and see if the formula holds.
Spoiler alert: It does.
For 1 it is simple:
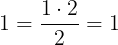
But that could be a coincidence. After all it is just 1 number, we did not really add up anything here, did we?
Let's try 2:
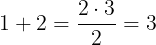
Seems ok. But could be because the 2 is also as a divisor in the formula. Better try 3 as well.
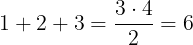
Ok, still holding up. Still pure luck?
If we continue this way we will get a good result all the time. But we can not simply try out all the numbers, there are infinitely many. Who is to say there is not some weird number up there for which the formula breaks?
When Gauß wrote down 5050 as his answer the problem at hand was solved. But could he use that formula every time when such a problem was presented?
This is where proofs come in and in the case of natural numbers, one option is Mathematical Induction.
How it works
Natural Numbers
Natural Numbers are positive whole numbers. The world of mathematics is actually divided by the question "Is zero a natural number?". So some might include zero and some might exclude it. For us it does not matter at this point. We just have to be clear on which side we stand (and this can even change, depending on what we want to prove).
Natural numbers are so important, they got their own symbol in mathematics. You might have seen the weird N before.
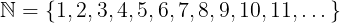
The most important fact about natural numbers is: They are lined up in a way so that every number has exactly one successor and we all agree and know what this successor is.
These are our domino pieces.
Tip one over
To tip our first domino piece over, we simply plug in a number, preferably as low as possible, and show that the formula works for that particular number. Remember, we already did that. We plugged in 1, 2 and 3. Does not get lower than one in our case (yes, zero would have worked as well, but what is the point there?).
So here it is again:
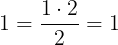
Let the others follow
Now comes the inductive part. We prove that if one piece of the domino set falls over (no matter which one), its successor will fall over as well. That is the key to our chain reaction. Because the successor has a successor of its own. And since we proved whenever a piece falls over, its successor will fall as well, this successor will follow. And that will go on and on and on and on ....
How do we do that in a mathematical way? We assume we have a falling piece and have a look at its successor. To make it easier to follow and not confuse the variable in the initial formula with our domino piece and its successor we give them a different name.
The assumed falling piece we call n and therefore its successor would be n+1.
Let us have a look at our formula:
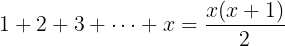
We want to prove that n+1 is falling over. So we plug in n+1 for every X in our formula. That would give us:
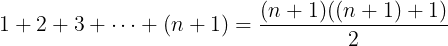
This is where we want to end up. But how do we get there?
We have to somehow make use of the fact that we know (assume) piece n is falling over. We know the formula holds for n and want to prove that it also holds for the successor n+1. Our task is to get hold of n and use the knowledge that the formula holds for n. We use that to prove it therefore also holds for n+1.
Let us start on the left side. That n+1 is the successor of n. Therefore we can rewrite the left side also including n as follows:
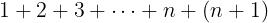
We know that the formula holds for n so we can plug that in and get an equation:
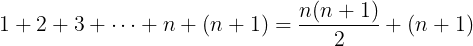
We took the 1+2+3+...+n and exchanged it for the equation. But there is also (n+1) added at the end. So we had to add that as well.
Using the knowledge that it works for n is essential for the proof. In our domino metaphor it is the fact that one of the pieces is in motion and falling over. What is left to do is to prove that the next piece is now falling as well. In our case, somehow arrive at the target formula for n+1.
For that we need some simple algebra. If we multiply (n+1) with 1 we don't really change anything. Luckily 1 can also be written as 2/2 and that is very useful in this case.
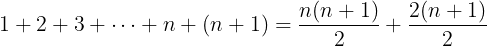
We are adding fractions with the same denominator so we can "pull them together":
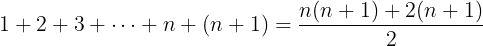
This looks promising. We are almost at the target formula but the nominator is not correct yet. Let us have a look at the nominator by itself:
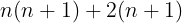
Notice that both terms of our sum have our successor piece (n+1) in them. We can pull that out.
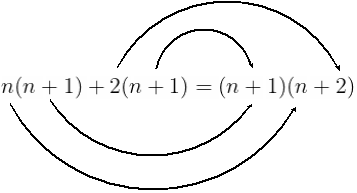
Since 2=1+1 and in addition it does not matter how you put parenthesis we can rewrite (n+2) as ((n+1)+1)
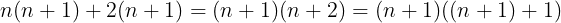
Eureka, we got it. Put that one back in where we pulled it out:
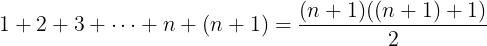
And there we have it. We proved that if the formula holds for one number n, then it also holds for its successor (n+1).
Since we already showed it holds for our first number n=1 it therefore must hold for its successor 2 and the successor that number, namely 3 and so on. Hence this formula is valid for every natural number, no matter how big it is.
Q.E.D.
If you want to show off a little bit, you can put
q.e.d.
at the end of your proof. It is the abbreviation of the latin phrase "quod erat demonstrandum" and means "that, which was to be shown".
Mathematicians put it to signify the end of a proof in bigger articles or to show they are done (or at least think so 😉).
Applications
The proof by Mathematical Induction can be a wonderful tool. Just remember that what you are about to prove has to be in bijective relation to the natural numbers. That means for every natural number there must be a corresponding result in your formula and vice versa.
For example you could prove that
For every natural power (no zero allowed) of 6 the result's last digit is 6
In this case the natural number with its successors is the exponent. Here are the first four examples:
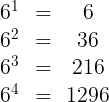
If you are interested in combinatorics, you can use Mathematical Induction for the following:
For X objects there are X! ways to arrange them in a specific order
If you are unfamiliar with the ! sign in mathematics, it is the combined product (aka faculty). That means 3! is 1x2x3=6 and 4!=1x2x3x4=24 and 5!=1x2x3x4x5=120 and so on.
To arrange 3 different objects (let us call them a, b and c) we can arrange them as
- a, b, c
- a, c, b
- b, a, c
- b, c, a
- c, a, b
- c, b, a
Those are the six ways to arrange three different objects.
For both theorems I will post the proof next week, until then have fun getting at them.
Have fun
I hope I could bring this method of proof and understanding it to a few more people. If you understood a little bit of it but not all, feel free to ask in the comments. Alternatively you can also look out for my post next week with the solution to the above mentioned theorems. Maybe that will give you the final "Aha-Moment".
Thank you very much for reading and remember: It's also supposed to be fun!
Header image picture taken by me.
Math pictures created with latex.codecogs.com
This was a lot of text and formulas to create. If I made a blunder somewhere along the line and didn't catch it despite proofreading several times, please let me know in the comments so I can fix it.
Edit: Corrected a typo in the last quote
Edit: Multiplying in text with the asterisk sign was interpreted by the front ends as cursive writing. Changed the multiplication sign to x.









