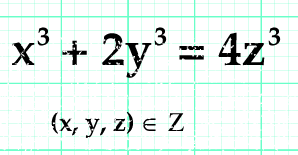
x³ + 2y³ = 4z³, (x, y, z) ∈ ℤ
| Español | English |
Solución:
( x, y, z ) = ( 0, 0, 0 ) |
|---|
Demostración:
Que ( 0, 0, 0 ) es solución resulta obvio, vamos a intentar encontrar otras posibles soluciones de la ecuación,
x ³ + 2y ³ = 4z ³ |
4z³ y 2y³, son ambos pares, lo que implica que x ha de ser par,
x1 = x / 2 8x1 ³ + 2y ³ = 4z ³ x1 ³ = ( 4z ³ - 2y ³ ) / 8 x1 ³ = 4(z / 2 ) ³ - 2( y / 2 ) ³ |
|
_\|/_ Este método de demostrar, por reducción al absurdo, la no existencia de soluciones, cada vez de menor valor, recibe el nombre de descenso infinito de Fermat |
|---|
Si ( x, y, z ) es solución, ( x/2, y/2, z/2 ) es solución también.
Reiterando este proceso, llegará un momento que encontraremos una raíz impar, lo cual es una contradicción, por lo tanto queda demostrada la no existencia de más raíces.
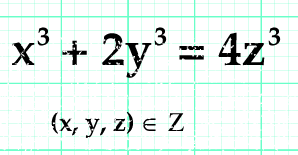
x³ + 2y³ = 4z³, (x, y, z) ∈ ℤ
| English | Español |
Answer:
( x, y, z ) = ( 0, 0, 0 ) |
|---|
Solution:
( 0, 0, 0 ) is a solution by inspection, we try to prove that is the only one solution,
x ³ + 2y ³ = 4z ³ |
4z³ y 2y³, are even, so x ought to be even also, if the equation has more solutions in integers,
x1 = x / 2 8x1 ³ + 2y ³ = 4z ³ x1 ³ = ( 4z ³ - 2y ³ ) / 8 x1 ³ = 4(z / 2 ) ³ - 2( y / 2 ) ³ |
|
_\|/_ This solution method, in which it is shown that any solution gives rise to a smaller solution, is known as the method of infinite descent |
|---|
if ( x, y, z ) is a solution, then so is ( x/2, y/2, z/2 ).
We could keep diminishing the solution as shown, and eventually arrive at a solution with an odd value, a contradiction.


