Hello math bugs(🐞) and hivers(🐝)
I hope you are strong and stout and doing great in life.
Once again I am back with another geometric problem.To prepare all the figures and and solution I did my best.You must have seen the problem in the cover photo.Check the problem once again and try to solve the it. Then step forward to the solution.
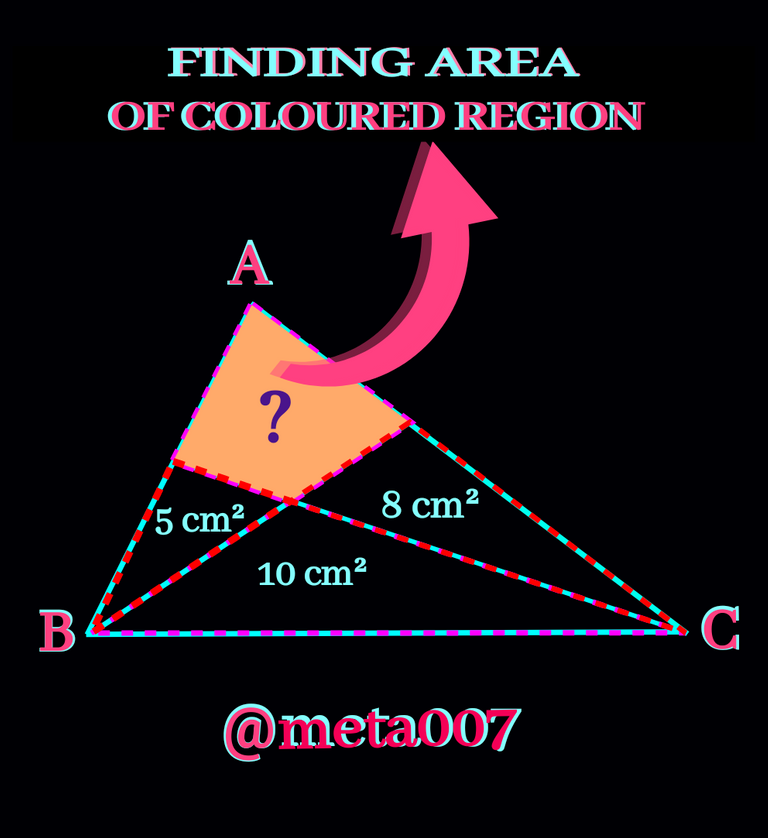
I have seen people have less interest to find solution.My moto is to convince them visualising the problem. That's why I always makes the figure colourful.If people do not like my work, hard work will be worthless. Let's see how people react to the article.
The first step is to draw a line as you can see it below in white color and thus the quadrilateral ADOE gets divided into two part i.e ∆ADO and ∆AEO. Let the area of ∆ADO and ∆AEO be a cm and b cm respectively.

The concept I am going to use as follows:
We know that the area of a ∆ depends on two things i.e the height and the base of a given ∆. The beauty of the concept is when height (perpendicular distance) equals, the ratio of bases becomes the ratio of area of the triangles.Check it in the figure below:
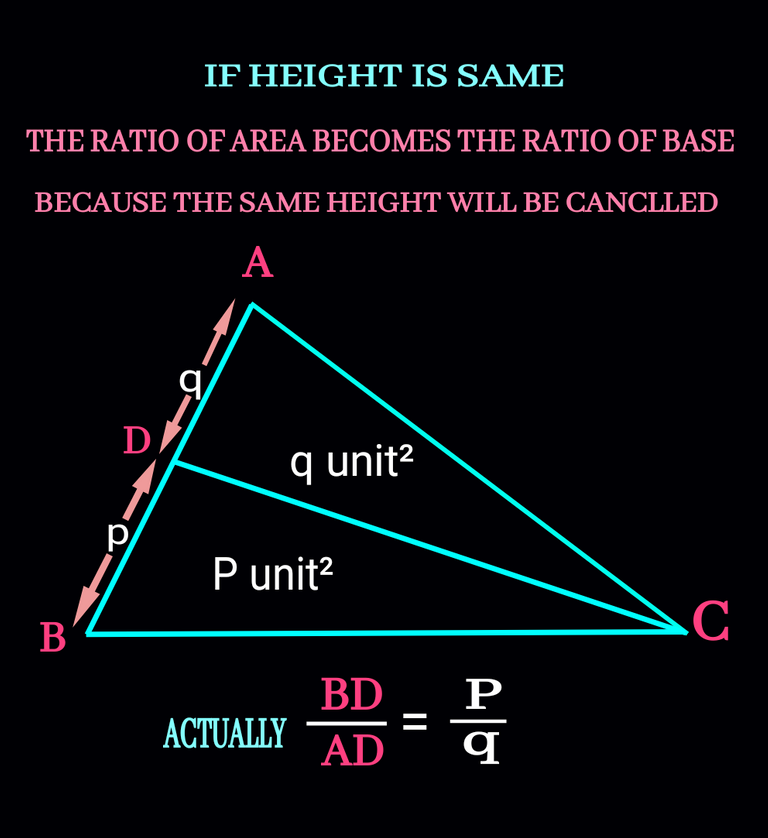
In the above figure raito of the sides BD & AD is equal to the ratio of area of ∆BDC & ∆ADC respectively.
The figure below contains the same element while the triangle are ∆CBE and ∆ABE.
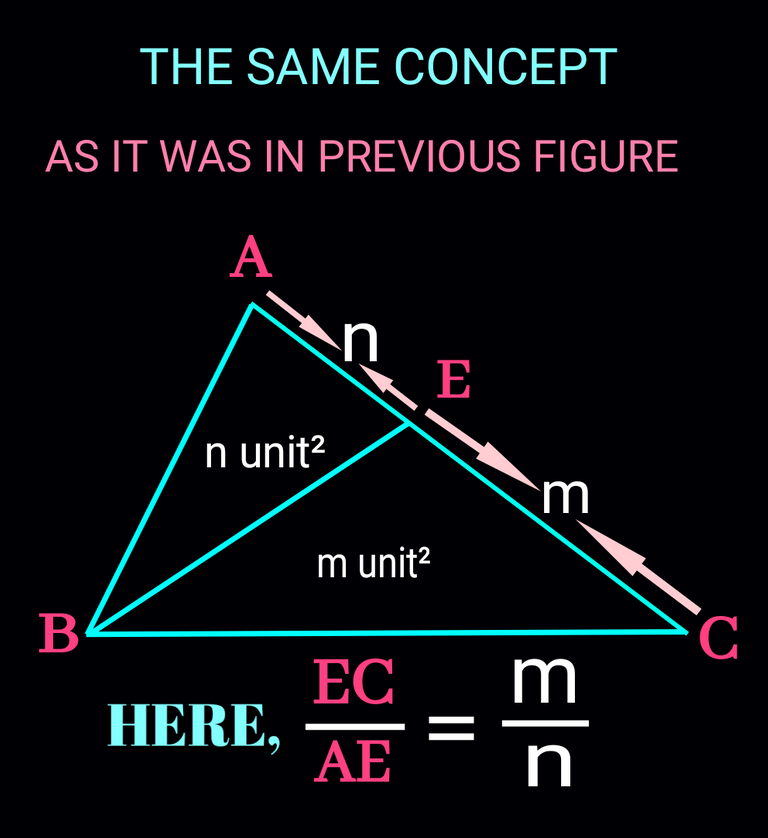
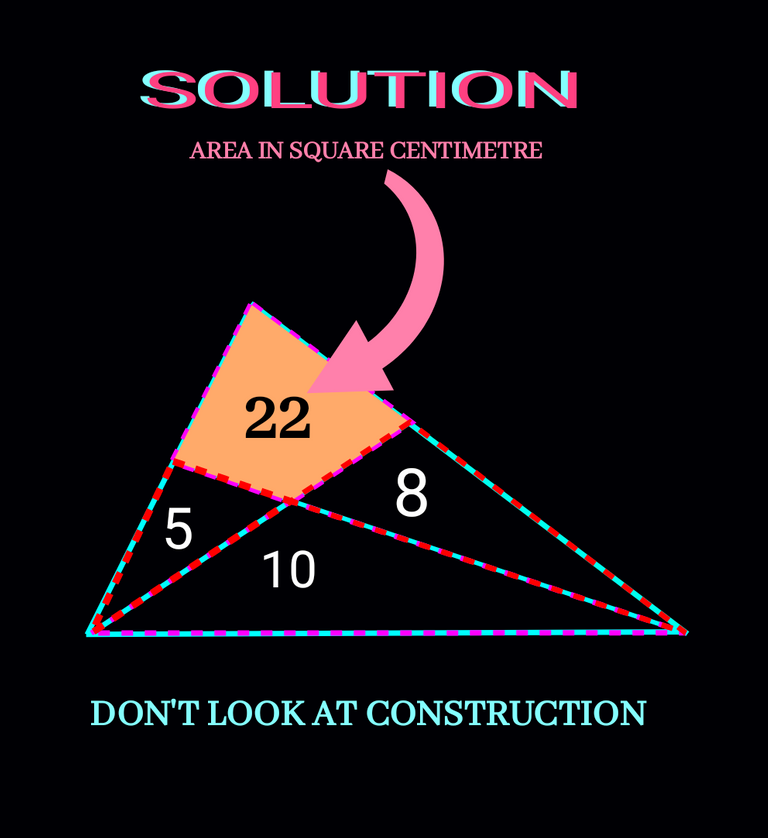
Solution as follows:
You can see two equation in the figure below.Both of them are made using the concept I mentioned in previous figure or in point.In the first equation ratio of AD & BD equals to the ratio of area of ∆ADC & ∆BDC. And in the second equation the same thing is done considering ∆AOC & ∆ABC.You can check it in the figure below as words may confused you.😂
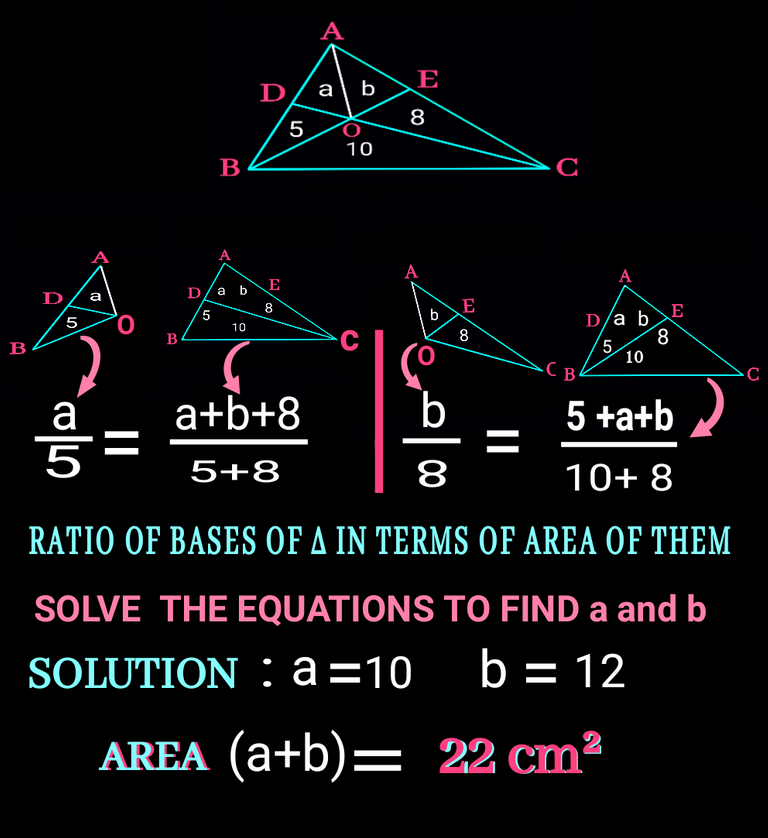
I solved the problem using just triangle property.
There are others ways also to solve it.
let's say mass point geometry. This concept can make it easier but many may not aware of it so I avoided it.If you want to know mass point geometry for a easier solution, make a comment right below the post.
Time for visualising our answer below:
Some links of my previous articles you may like them
Problem on angle bisectors of a ∆
I hope you liked today's problem and the solution.
Thank you for so much for visiting.
Have a nice day
All is well
Regards: @meta007




