Part I: Beavers vs Rhinos

The rise of decentralized systems of value transfer such as crypto tokens has brought the need for effective systems of decentralized governance. Amid those systems, fractal democracy shines as the protocol that attempts to defeat Pareto inequality, prevent the formation of cartels and do so while promoting free market economy in the public goods and services space.

Some fractal democracy proponents have highlighted several of its perceived shortcomings though. Most of these concerns have to do with the difficulty of correctly appraising the work of their fellow members; let alone, determining the quality or the mid/long term implications of those contributions. Also, an inefficient incorporation of quality proposals has been emphasized. These concerns are brought by Fractal Democracy enthusiast, who happen to worry about building the whole protocol with insufficient rigor, or over weak foundations that won't be able to guarantee its long term effectiveness. In this article, just for the sake of it, I'll refer to this group as the Beavers.

Other members of the community, which I'll call the Rhinos, have a different stance. They believe that the recurrent nature of the process furnishes it with statistical traits that, given enough measurements, will lead to an accurate assessment of the overall contribution of each member. In Probability Theory, such a rationale is called the Law of Large Numbers; it is mathematically correct and conveniently attractive for practical implementations.

However, when dealing with the Law of Large Numbers, one has to remember that, it is valid in the long run of experiments only. Long run means in the limit when the number of measurements goes to infinity. In the case of Fractally, this would require a large number of breakout sessions. At a rate of one session per week, this could mean a really long time. Also, very importantly, in the interval between now and that future time when we will have a fair estimate of the actual value of members' contributions, anything can happen. And because of the complex nature of the system, this anything is really important.

To better understand all this, let's begin with a very simple statistical example. let's consider the simplest possible experiment. Let's toss a fair coin 1000 times and let's suppose that we are interested in measuring the number of heads so obtained. Everyone knows that on average this number will be 500. However, that doesn't mean that, at any realization of the experiment, the number of accumulated heads will be exactly half the number of tosses. Quite the opposite, during the first run the experimenter could obtain 511 heads and 489 tails. Such an observation wouldn't take anyone by surprise. The problem is, in complex systems such as the ones EOS, Eden and even Fractally already are, these deviations from the mean can be very, very relevant.

It is a well known result from network science that little variations, at any given time in a complex system, can drastically affect the future behavior of that system. Such result is known as the "Butterfly effect" and appears in most complex networks: from climate, to fractals, to social platforms, to markets, everywhere.

The whole cryptospace is an example of a complex system and, as I mentioned in my previous post, it is run via a huge Fractal democracy protocol. "What are you talking about?" the reader may say. "Fractal governance is something absolutely new! It has never been tried before!". Well, think about it: Every second, millions of participants in the cryptospace achieve consensus on the perceived value of crypto projects; that consensus is called market-cap ranking. Instead of having breakout rooms, users get into websites (YouTube, CoinDesk, etc) in which they (semi-randomly) get in touch with the recent value propositions of different projects. Each member assigns some "respect" to those random projects by deciding how much to invest in each of them. This doesn't happen weekly as in Fractally, but every second. So, according to the Law of Large Numbers, the global crypto market should arrive to correct valuations much faster than the Fractally community. Yet, you frequently observe some pretty catastrophic events on the global cryptospace.

In the cryptospace analogy of Fractal Democracy, the Beavers would point out that there is an immense difficulty separating the wheat from the chaff and therefore, best practice protocols for quality assessment are needed to avoid getting crushed by the market. On the other hand, according to Rhino's perspective, in the long run the market will correctly identify the best projects and rank them fairly. As I stated above, the Rhinos are mathematically correct; but that doesn't prevent that, in the mean time, some pretty incorrect rankings occur. Furthermore, the effect of a single one of those miscalculations can be immensely painful to the incumbents; take the Luna fiasco, or more recently Celsius, as rutilant examples of this.

So, inefficiencies in value/quality assessment can create calamitous events in free markets. In other words, just as the number of tails can significantly deviate from the expected value when tossing a coin, so the valuation of a project/contribution can significantly deviate from reality when performed by regular people. But, unlike the tossing of the coin, markets are complex systems. Therefore, the implications of those temporary deviations can be dramatic, butterfly effects at their best.

Part II: Networks vs Networks

There is an additional quirk in the case of Fractal Democracy: The whole system aims to become a network of networks. Each of these networks will likely be governed by its own tweaked version of Fractal Democracy. These networks will be competing for resources from whatever space they happen to meet with each other. The winners of those resource battles will be the networks that most efficiently discover and integrate value and value producers. One example of those resources being competed for is people. People will naturally flock to fractals that are better at valuing and incorporating their contributions, not in the long run, but now. So, it is in the best interest of nascent Fractal Democracy communities to tweak their value discovery and allocation protocols to perfection as much as possible

In this post, I attempt to provide a simple mathematical framework by which to characterize the whole Fractal Democracy process. It is by no means exhaustive, but it aims to help as input to the simulation efforts being conducted by some other members of the community.

Part III: Introducing the model

The greater Fractally ecosystem is being designed as follows:

1. The ecosystem consists of a set of communities.
2. Each community has at least one array of meetings in which a token of respect is given, to each of the participating members, by community consensus.
3. It is assumed that this respect token is considered by most participants as desirable to acquire .
4. Each participant has some level of selfishness.
5. Each participant periodically reports his contributions to the community. This is done during the meetings introduced in (2).
6. Each participant has some level of understanding of the current state of the network.
7. Each participant has some individual capacity to grasp the implications that any contribution from any other participant will have on the network.
8. At each meeting, the amount of respect a participant earns depends on his ability to articulate his contributions and their corresponding implications to the network.

Now, consider the case of one of such communities mentioned in 1). Let:

• i: denote the ith member of this community.
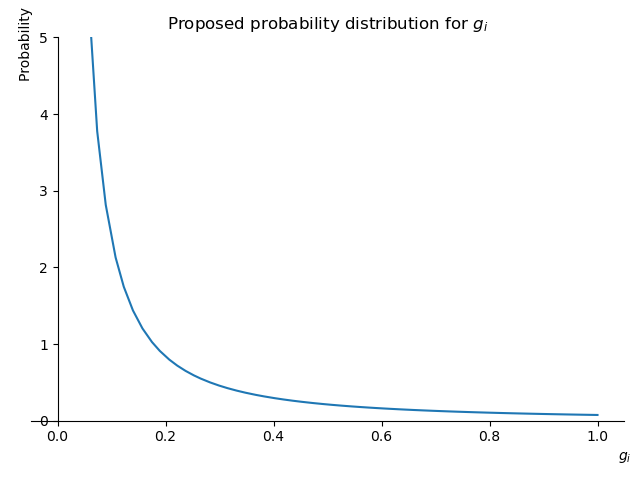
• g(i): denote member's i level of information about the current state of the network. Let 0 < g(i) < 1. So, g(3) = 1 means that member 3 is like a hard disk that stores every possible bit of information about the network; every technical detail, every incentive on every participant, every little piece of data about all resources from every actor, etc. On the contrary, g(4)=0 means member 4 is a total newbie.
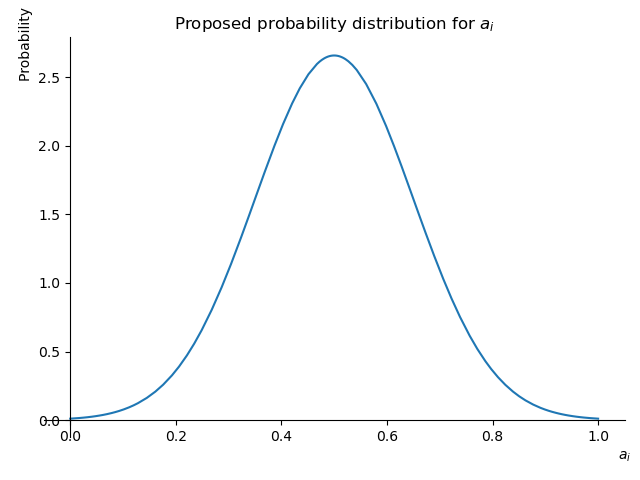
• a(i): the analytic capacity that member i has, and that allows him to grasp some of the implications that every little small contribution from every other member will have, at any time frame, on the community. a(i) is a variable that depends on member's i brainpower, computational power, overall knowledge about a multitude of disciplines such as game theory, economics, sociology, human psychology and many other factors. a(i) is also a continuous variable in the range [0, 1]. Having a(5) = 1 means that member 5 is as smart as a super powerful AI that, given the appropriate data, can accurately predict the future state of the network.
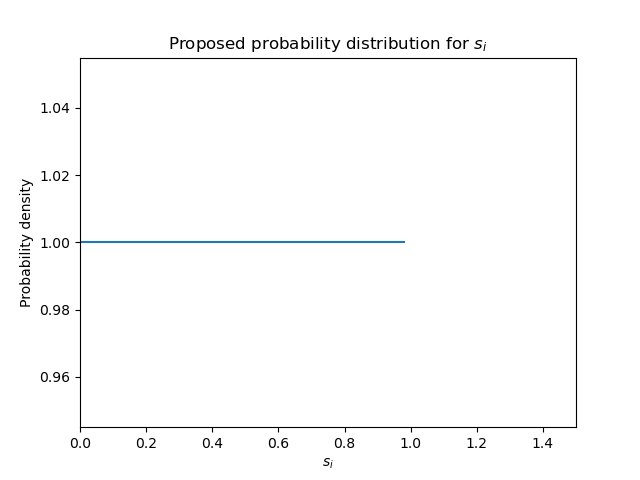
• s(i): denote the level of sincerity of member i. As with the other variables, let 0 < s(i) < 1. Where 0 represents total mythomaniac deceitfulness and 1 represents absolute brutal honesty. So, for example, s(i) = 0.4 would mean that member i is somehow prone to lying or exaggerating.

Restricting the value of these variables to the [0, 1] interval allows us to interpret its values as probabilities. For example, g(4) = 0.32 can be interpreted as having a 32% probability that member 4 has the correct and complete information of what he is talking about at the exact moment he is assigned that value. Also, s(16) = 0.85 can mean that the odds of member 16 being truthful at that moment are 85%.

Of course, all of the above parameters vary from person to person. So, each of them is a function of i. But because it is not feasible to know the exact form of these functions, and this is true especially in the long run, we can model them as random variables defined, all of them, on the interval [0, 1]. The actual value for each of these parameters, for each member, can be estimated via polls done within the community or simulated via random number generators.

Next, let's delve into the specific form of the distributions of these random variables. In the case of g(i), one would say that the vast majority of people, even millions of them know very little about the details of the communities they are entering. For example, the vast majority of members of the EOS community don't know even close to 10% of everything that there is to know about EOS. Also, one may think that this becomes even truer as the protocols and smart contracts of these communities get more complex over time. Some people will have above average knowledge of the system and only very few of them will be experts. So, the most logical for g(i) should be a Pareto distribution that, over time, becomes ever more long-tailed.

In the case of a(i), because it represents a measure of overall intelligence, one could argue that a simple normal distribution centered at 0.5 and with a standard deviation around 0.15 should do it.

As for s(i), because it represents a measure of sincerity, one could examine the incentives each member faces when presenting his work to the community: On the one hand, during any meeting, because reputation and self image are at stake, participants have the immediate incentive to only mention, and even exaggerate, the positive aspects of their contributions. This is especially true during initial stages of community development, when verification and validation mechanisms are not yet in place. So, this incentive should shift the mean of the s(i) distribution towards the left of the [0, 1] interval.

On the other hand, the fellow members who are ranking the contribution, have the incentive to not be too critical about any presentation because they themselves will be ranked by those they criticize. This is another incentive that shifts the mean of s(i) to the left, closer to 0.

There is a third incentive that every participant has to not allow low quality contributions into the system they have themselves invested in. This incentive pushes the mean of the distribution to the right and it has the peculiarity that it varies a lot from person to person because it strongly depends on how much each individual has invested in the community.

In short, because we have incentives pushing the average both to the right and to the left, at least one of which can be really noisy, we can suppose that s(i) has the highest variance of all the above defined parameters and we have no idea where its mean could be located. Thence, a uniform distribution for s(i) in the [0, 1] interval should be adequate. Alternatively, a normal distribution with a pretty large variance and truncated to the interval [0, 1] could be used. Whatever the case, of all parameters, s(i) seems to be the one that contributes the more noise to the system and, therefore, more likely to generate detrimental butterfly effects.

There we have a really nice first result from our analysis: Because s(i), the individual level of sincerity, adds the most noise to the system, and because it appears as a consequence of asking people to verbally showcase their contributions to their peers, it would be better to simply minimize this aspect in the protocol. Instead, try to find a way so that weekly ranking is based on already delivered products; with only minimal or even null verbal intervention from the person being ranked. In order to do this, the format of the breakout sessions could be modified. Additional restrictions such as preventing self-ranking which, by the way, has the added benefit of forcing everyone to think deeper about peer's contributions, could help in this direction.

Having established the properties of g(i), a(i) and s(i), we can now used them to the define more interesting quantities. Let, for example J(i) = g(i) * a(i) be the level of judgment member i has about the network. Clearly, if g(4) = 0.6 and a(4) = 0.9, meaning that member 4 only knows 60% of everything that can be known about the current state of his fractal, then even if he is as brilliant as having 90% the brainpower of a general super A.I., he can only have J(4) = 0.6*0.9 = 0.54 judgment about the system. That is, despite all his computational power, due to data bottlenecks, member 4 will have only a 54% probability of being right about how his fractal is going to evolve over time.

Using all these tools we can construct some powerful indicators about the current state of any fractal. Let:

< g > = ∑ g(i)/N
< a > = ∑ a(i)/N
< J > = ∑ J(i)/N

Then,

• < g > can be interpreted as the level of information the whole fractal has about itself. Also, and very interestingly,
• < J > should be an indicator of how accurate is the whole fractal's judgment about itself.

Thence, if < J > is a measure of how accurate the judgement of community, as a whole, is about its current state, then < J > should also indicate how likely is that community to self adapt and thrive. So, from my perspective, < J > is a good candidate for optimization in any simulation and, of course, in the real system.

Additional quantities can be defined using sincerity levels, selfishness levels or any other variable that one wants to add. However, as said above, some of them would mainly add noise to the system and reduce the predictive power of the model. Further analysis and tuning would be required in that direction.

Conclusion

The rising of different protocols for decentralized transfer and store of value has led to the need for decentralized forms of governance. Amid fierce competition among these governance systems, fractal democracy can only flourish if it manages to efficiently incorporate its best participants' contributions and fairly distribute its resources. If that comes to past, then, from the author's perspective, competition between different fractals will also be inevitable. It is my hope that this article has served to inspire some new ideas about how to best tackle these new challenges.