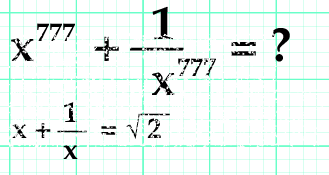| Español | English |
Enunciado
Solución
x + 1/x = √ 2 , |
|---|
Este problema se puede resolver empleando las propiedades de las funciones simétricas.
Una función es simétrica, si intercambiando cualesquiera de sus variables el valor de la función no varía |
x = α , 1/x = β
α + β = √ 2
α ∙ β = 1
Como es bien conocido, relaciones de Cardano-Vieta , α y
β son raíces de la ecuación,
ξ 2 − √ 2 ∙ ξ + 1 = 0
α = √ 2 /2 ∙ ( 1 + i ) = е i ∙ π/4
β = √ 2 /2 ∙ ( 1 − i ) = е − i ∙ π/4
Sólo resta evaluar α y β elevadas a la 777 potencia,
777 = 4 ∙ 194 + 1
е π ∙ 777/4 = е π ∙ 194 ∙ е π/4 = е π ∙ 2 ∙ е π/4 = е π/4
∴ x 777 = x
De dónde,
1 |
|---|
∎
| English | Español |
Statement
Answer
x + 1/x = √ 2 , |
|---|
This is a problem on symmetric functions.
A function is symmetric if the exchange of its variables does not alters its value |
x = α , 1/x = β
α + β = √ 2
α ∙ β = 1
As it is well known, Vieta's formula , α and
β are roots of the equation,
ξ 2 − √ 2 ∙ ξ + 1 = 0
α = √ 2 /2 ∙ ( 1 + i ) = е i ∙ π/4
β = √ 2 /2 ∙ ( 1 − i ) = е − i ∙ π/4
Evaluating α and β to the 777 power,
777 = 4 ∙ 194 + 1
е π ∙ 777/4 = е π ∙ 194 ∙ е π/4 = е π ∙ 2 ∙ е π/4 = е π/4
∴ x 777 = x
Whence,
1 |
|---|
∎
Media