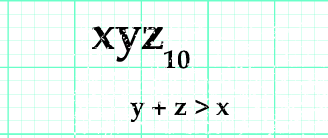| El usuario @ydavgonzalez bajo el lema El ejercicio del día propone problemas de índole matemática a ser resueltos por los lectores. En esta ocasión trataremos sobre la resolución del problema del dìa doce de junio de 2024 |
|---|
¿Cuántos números de tres cifras existen cuya suma de las primeras dos cifras es mayor que la tercera cifra?
Este tipo de problemas se presta de forma natural a su resolución mediante la aplicación de la fuerza bruta.
Intentaremos la resolución analítica del ejercicio propuesto.
{ ≤ } ⋂ { > } = ∅
Solución analítica
No solucionaremos el problema original, sino otro problema relacionado, más sencillo ...
¿Cuántos números de tres cifras existen cuya suma de las primeras dos cifras es menor o igual que la tercera cifra? |
|---|
Estudiemos el problema en función del valor de la cifra de las centenas,
| n | 1 | 2 | ... |
|---|---|---|---|
| Menores | 1 | 3 | ... |
| Iguales | 2 | 3 | ... |
| cn | 3 | 6 |
⋃ { i, (n - i) }
0 .. n
Dada una centena, n , la cantidad de números con suma menor es el valor para la centena anterior, cn-1 .
cn , la cantidad de números menores o iguales.
Con suma igual, las disposiciones, cero incluido hasta la centena correspondiente, n + 1.
Sucesión recurrente
Obtenemos la siguiente sucesión,
Definiendo el valor de c0 como,
Podemos escribir esta otra sucesión,
El término general de ésta,
Restando cn de cn + 1 ,
c n + 1 - cn = cn - cn - 1 + 1
c n + 1 = 2cn - cn - 1 + 1
Restando cn + 1 de cn + 2 ,
c n + 3 = 3cn + 2 - 3cn + 1 + cn
Hemos obtenido una ecuación recurrente que describe nuestra sucesión.
|
_\|/_ Dada una sucesión un , supongamos que podamos expresarla como una ecuación recurrente, un+k = a1un+k-1 + a2un+k-2 + ... + akun Podemos demostrar que la serie de la sucesión es también recurrente y verifica la ecuación, sn+k+1 = (1 + a1)sn+k + (a2 - a1)sn+k-1 + ... - aksn Observemos que, u1 = s1 , u2 = s2 - u1 , ... ... un = sn - (u1 + ... + un-1) = sn - sn-1 Sustituyendo los valores de la sucesión, en función de los valores de la serie, y simplificando se llega a la expresión de los coeficientes de la serie en función de los de la sucesión. |
|---|
La serie de nuestra sucesión,
Podemos expresar nuestra serie como una serie de potencias,
Para determinar los coeficientes Bn , resolvemos un sistema de ecuaciones que generamos a partir de n + 1 valores de sn y la ecuación anterior.
Serie,
n³ + 6n² + 11n + 6
sn = ―――――――――
6
Hemos determinado el término general de la serie de las sumas de los n + 1 primeros números naturales , que quizás nos sea de utilidad en otro momento y otro lugar ...
La solución de nuestro problema,
ya que existen 900 números de tres cifras y c0 no forma parte de nuestro problema.
Solución:
Fuerza Bruta
Utilizando Maxima ,
| 💻Sesión Maxima | |
|---|---|
(%i1) load ("stringproc")$ (%i2) strings: makelist (printf (false, "~d", i), i, 100, 999)$ (%i3) octets: maplist (string_to_octets, strings)$ (%i4) zero: string_to_octets ("0")[1]$ (%i5) result: apply ("+", maplist (lambda ([x], is ((x[2] + x[3] - zero) > x[1])), octets)); (%o6) 219 false + 681 true
|
Amablemente, Maxima, nos informa de que, de los 900 números de tres cifras, la suma de las dos primeras cifras es mayor que la primera cifra en 681 de ellos y no lo es en otros 291.
Hecho, que podemos corroborar mediante la solución analítica del problema ∎