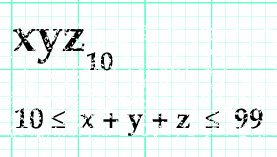| El usuario @ydavgonzalez bajo el lema El ejercicio del día propone problemas de índole matemática a ser resueltos por los lectores. En esta ocasión trataremos sobre la resolución del problema del dìa doce de julio de 2024 |
|---|
Enunciado
¿Cuántos números de tres cifras existen cuya suma de cifras es un número de dos cifras?
Este tipo de problemas se presta de forma natural a su resolución mediante la aplicación de la fuerza bruta .
Intentaremos la resolución analítica del ejercicio propuesto.
Solución analítica
No solucionaremos el problema original, sino otro problema relacionado, más sencillo ...
¿Cuántos números de tres cifras existen cuya suma de cifras es un número de una cifra? |
|---|
La suma de las cifras de un número de tres cifras es como máximo 27, 9 + 9 + 9, de forma que la suma de las cifras de un número de tres cifras es un número de una o dos cifras.
Existen menos números de una cifra.
Estudiemos el problema en función del valor de la cifra de las centenas.
Sea c la centena correspondiente, u unidades y decenas d, han de sumar lo necesario para que el resultado total sea un número de una cifra.
c | u + d |
1 | 0 ... 8 |
2 | 0 ... 7 |
... | ... |
9 | 0 ... 0 |
|
⠀⠀⠀⠀ _\|/_ El número de formas de sumar n |
|---|
Como es posible deducir sin dificultad, sumando para las centenas, obtenemos como resultado la suma de las sumas
de los nueve primeros números naturales.
La serie de las sumas de los n + 1 primeros números naturales , la determinamos ya en otra ocasión ,
n³ + 6n² + 11n + 6
sn = ―――――――――
6
La solución de nuestro problema,
990 - s8 = 900 - 165 = 735
Fuerza Bruta
Utilizando Maxima ,
| 💻Sesión Maxima | |
|---|---|
(%i1) load ("stringproc")$ (%i2) strings: makelist (printf (false, "~d", i), i, 100, 999)$ (%i3) octets: maplist (string_to_octets, strings)$ (%i4) zero: string_to_octets ("0")[1]$ (%i5) sums: maplist (lambda ([x], lreduce ("+", x)), octets - zero)$ (%i6) apply("+", maplist(lambda ([x], is(x > 9)), sums)); (%o6) 165 false + 735 true
|
Amablemente, Maxima, nos informa de que, de los 900 números de tres cifras, la suma de todas sus cifras es un número de dos cifras en 735 de ellos y no lo es en otros 165.
Hecho, que podemos corroborar mediante la solución analítica del problema.
∎
Media