Air traffic controllers, physicists, and video game creators do not have a lot in common, except for the basic concept of "Vectors." You've undoubtedly heard this term thrown about a lot but perhaps you're just like me and you just aren't really sure what it means. That's fine; this post will likely answer a few of our questions. What exactly are vectors? And why should they be important to anyone?

{vec {a}} is a vector from point A to B. ; Author ; License
First and foremost, we must grasp the concept of "scalars," which means "quantity with magnitude." Scalars are units of measurement that tell us how much of anything there is. The distance between you and your television, for example, is scalar, as is the volume and temperature of the coffee you most likely drink in the mornings.
The magnitude of vector quantities is also accompanied by an additional piece of information known as "direction." You'll need to know how far away and in which direction your kitchen is in order to go there and create some pancakes. This time, it's not just the distance that matters, but also the displacement.
Because vectors do not change depending on perspective and remain invariant to the coordinated system, they are highly unique and valuable in a variety of domains. You might be wondering what that means.
This question can be answered by taking a cue from this: if you and your friend are standing on opposite sides of a box you want to move. This means you're facing opposite directions. If your friend takes two steps to the right and three steps forward while you take two steps to the left and three steps back, you'll likely feel like you're moving in different directions, but in reality, you've both moved the same distance in the same direction by following the same vector. The vector remains constant and unchanged regardless of which way you face or which coordinate system you set over the ground.
Taking a look at the x and y axes of the well-known cartesian coordinate system. Because both directions are utilized to define everything we graph, they are referred to as the coordinate basis. Moving the box from point A to point B produces a vector from point A to point B, which can be expressed mathematically as 2x + 3y or as an array (2,3). Your coordinate basis points in the opposite directions as your friend's and can be written as -2x'-3y' or as an array if you're looking the other way (-2,-3).
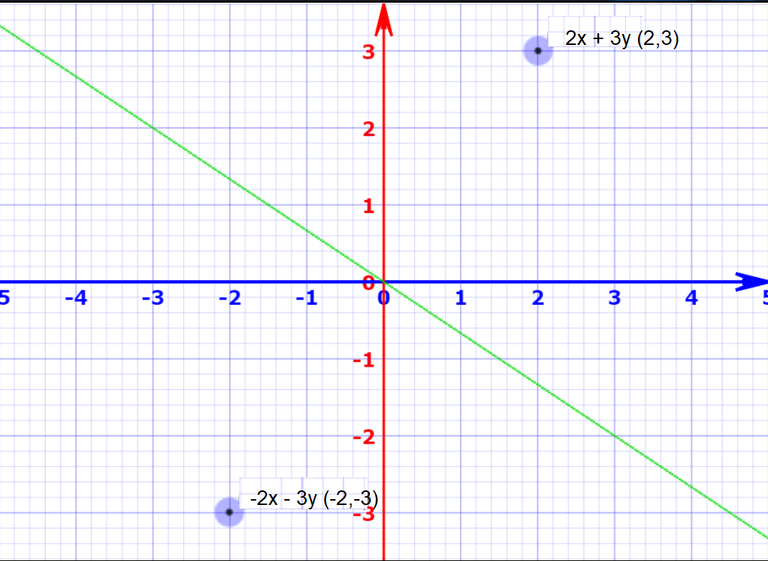
[Source:@mengene)
The arrays are clearly not the same, yet a vector cannot be described entirely by an array. Each array requires a basis to provide context, and when they are appropriately assigned, it is clear that they are describing the same vector. Individual elements in the array can be thought of as letters, and just as a sequence of letters can only make up words in a specific language, when given a coordinate basis, an array takes on the meaning of a vector. Similarly, distinct representations from two bases can describe the same vector, just as different words in two languages can express the same meaning. The vector is the essence of what is being communicated, regardless of the language used to describe it.
Because all quantities with this attribute are members of a group called Tensors, scalars likewise have this coordinate invariance property. Varying forms of tensors hold different quantities of data. One might wonder if this suggests that something other than vectors can transmit more information. Yes, most definitely!
Even if you have forces working in the same direction with equal amplitude depending on how they are oriented, you might witness waves or whirls if you were to develop a video game and you'd like to genuinely simulate how water behaves. Orientation is achieved by combining force (which is a vector) with another vector. The physical quantity "stress," which is an example of a second-order tensor, is a physical quantity.
A clip of how Tensorflow is applied in Building A Video Game
Outside of video games, tensors are utilized for a variety of applications, including scientific simulations, car design, and brain imaging. Scalars, vectors, and the tensor family provide a very simple means of understanding complicated ideas and relationships, and they are a prime example of mathematics' elegance, beauty, and essential usefulness.
Thanks for reading through!
More interesting reads can be found here:
An introduction to vectors
Vectors
Scalars and Vectors
Applications of Vectors in Real Life, Engineering and Physics.
Posted from HypeTurf
