Hello math bugs(🐞) and hivers(🐝)
I hope you are strong amd stout and doing great in life
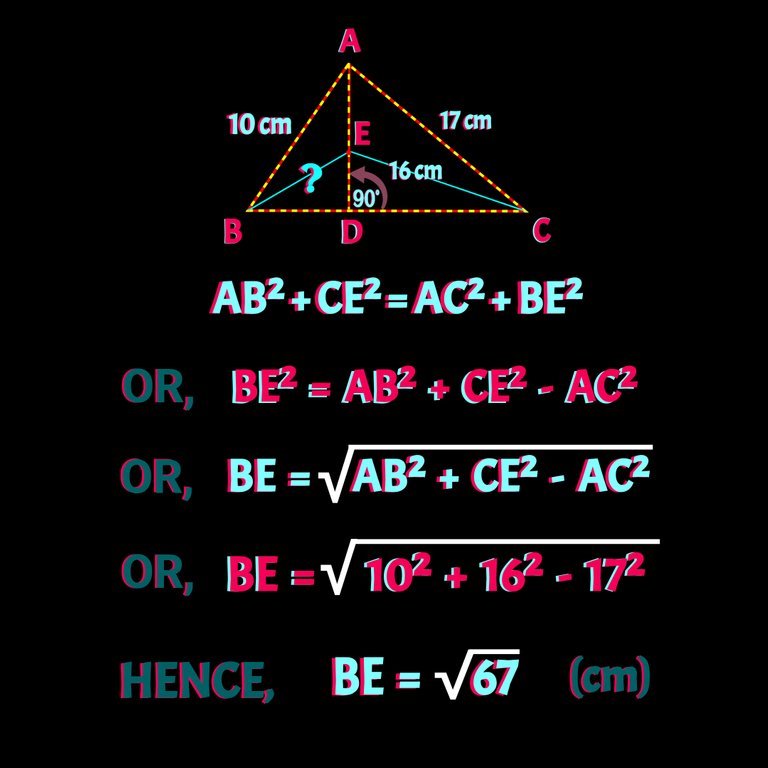
Well come to another intersting gemetric problem and its solution. ∆ABC is a random triangle. AD is perpendicular to BC and E is a random point on AD. If *AB =10 cm , AC= 17 cm and CE =16 cm, What is BE? Check the figure down below:

This is a true use of pythagorean triplet .Today we need no other concept except it. If we use pythagorean trip on triangles on the problem figure, a sweet relation must come out and whcih is given by AB²+ CE² = AC² + BE². I'll proof it, once we get to the answer.
Check the following window for value of be BE
Let's prove it
We gonna use pythagorean triplet in ∆ABD and in ∆CDE.
From ∆ABD
We have AB² = AD² + BD²...equation (1)
From ∆CDE
We have CE² = CD² + ED²...equation (2)
Now, after adding equations (1) and (2)
We have AB²+ CE² = AD² + CD² + BD² + ED²...eqn (3)
Again, using pythagorean teiplet on ∆ADC and ∆BDE,
We can say
AD² + CD² = AC² and BD² + ED² = BE²
Now, if we replace AD² + CD² and BD² + ED² in equation (3) by AC² and BE² respectively, we can have
AB² + CE² = AC² + BE² (proved)
Check the following figure also if you missing out something

For replacing check this one

All the figure are used here made by me using android application. There may be some construction misatke(s) or they may not be proper drawing. It takes time to make those figure. If you find any dispute, please ingnore it and cosider the data only.
I hope you find this post interesting and understandable.
Thank you so much for visiting
Have a nice day
All is well
Regards: @meta007




