Hello math bugs(🐞) & hivers(🐝)
Well come to another episode of geometry. Today, I have come up with a problem on similarity. It is very easy of you did this before.
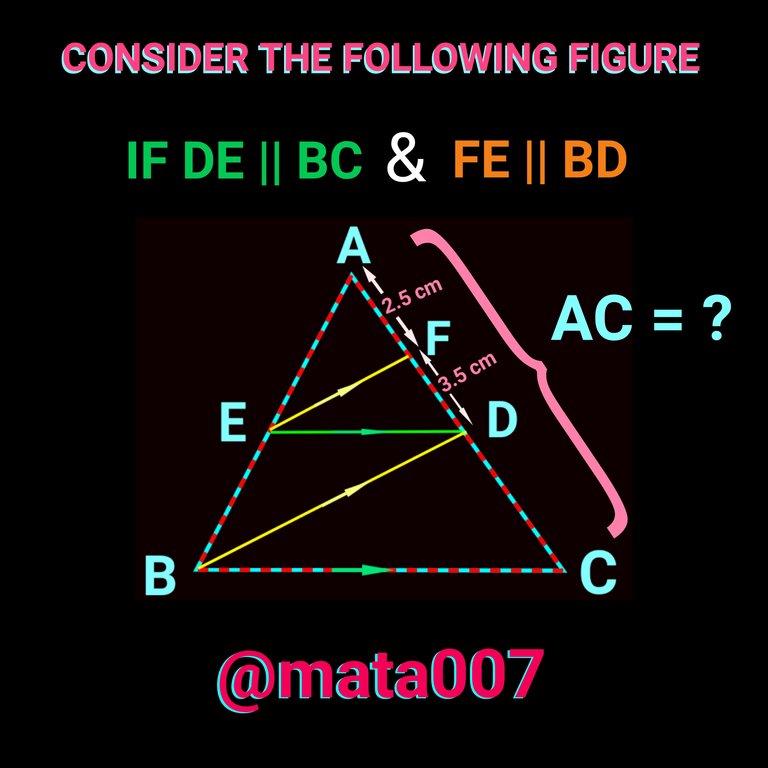
At first, let me elaborate the question a little bit. Here is random trinagle called ∆ABC. D and E are two points on sides AB and AC respectively drawn such a way that DE is Parallel to BC. D is also a point on AC such that AF becomes 2.5 cm and FD becomes 3.5cm. Here EF is also parallel to BD as you can see in the problem figure given below. Now, You have to find the value of AC
The only thing you need to know here is Thales theorem. So, let me explain it first, then I'll go to soluion.
Thales theorem:
The basic concept is if a parallel line of any side of a trinagle is drawn, the line cut the other two sides in equal ratio. It is also called basic proportionality theorem. Check the following figure 👇
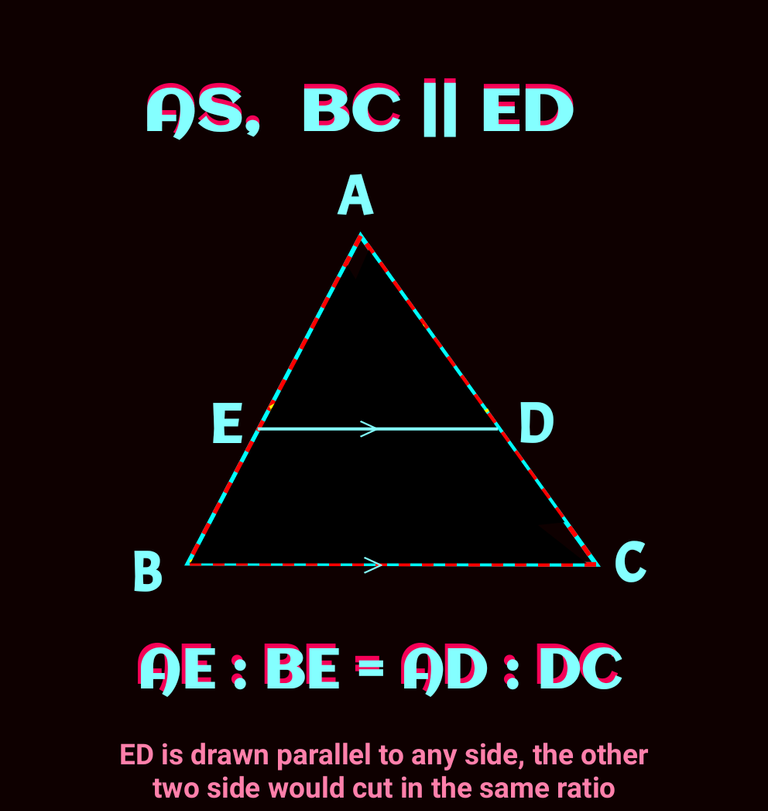
It can be proved using similarity. Let's do it
In the above figure, you can see two triangle namely ∆ABC and ∆AED. If we compare angles of them , we can see all of the respective anagles are equal.
∠BAC = EAD [ common angles]
∠ABC = ∠AED [ similiar angles as BC||ED and AB transversal]
∠ACB = ∠ADE [ similiar angles as BC||ED and AC transversal]
Hence, ∆ABC ~ ∆AED
So , the ratios of correspoding sides are equal.
Note:
✍️ Reverse of thales theorem is also ture: If AE/EB= AD/DC then ED || BC
✍️We not only get AE/EB =AD/DC, we can have other ratios: AB/AE = AC/AD or AB/EB =AC/DC
✍️If the points E and D would be mid points of AB and AC respectively, the ratios would 1:1 and in that case ED would be half of BC.
SOLUTION:
First, fonsider ∆ABD. In ∆ ABD EF|| BD so AF : FD = AE : EB or AF : AD = AE : AB. As we need to find AC , then 2nd one will work well. So we can say as follows:

AE : AB = AF : AD
Or, AE : AB = AF : (AF + FD)
Or, AE : AB = 2.5 : (2.5 + 3.5)
Or, AE : AB = 2.5 : 6
Or, AE : AB = 5 : 12
Let AE = 5y cm and AB 12y cm
Now, in ∆ ABC ED || BC , so again we can say AE : AB = AD : AC. Check it below👇
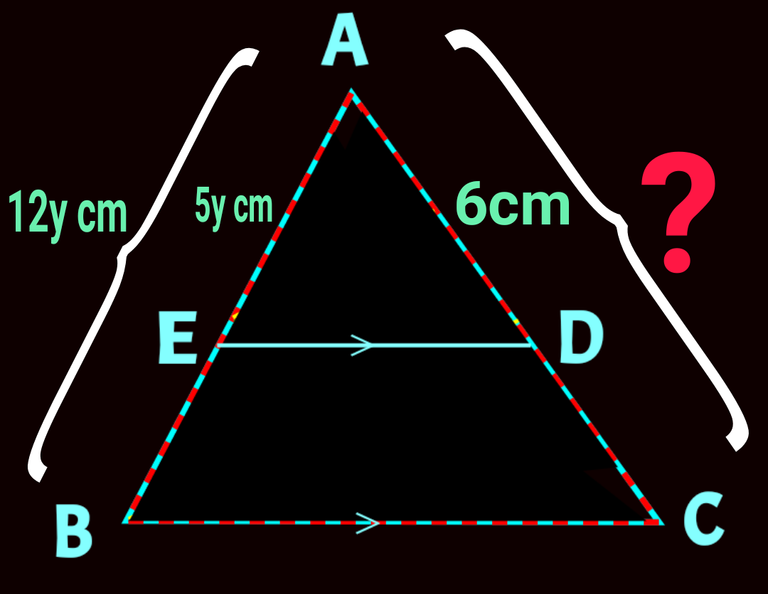
AE : AB = AD : AC
Or, 5y : 12y = 6 : AC
Or, AC = 12y × 6/ 5y
Or, AC = 72/5
Or, AC = 14.4 [ cm]
If you understand stand thales theorem or similarity, the problem can be done in seconds.
Short cut approach:
Direct from problem figure
5 units = 6 cm
1 unit = 6/5 cm
12 units = 6/5× 12 cm
So, AC = 14.4 cm
🎤🎤Figures used here may mot be accurate, try considering just the value given. All the figures are given here are made by only.
I hope you liked my explanation
Thank you so much for visitng
Have a great day
All is well
Regards: @meta007
