Hello maths bugs(🐞) & hivers(🐝)
Well come back to another intersting geometric problem with it's beautiful solution. There is large ∆ABC whose whose sides are AB= 13 cm, AC = 14 cm and BC = 15 cm. You have to find area of smaller ∆BOC enclosed by BO, CO and sideBC. Before heading to the solution, give it a try first.
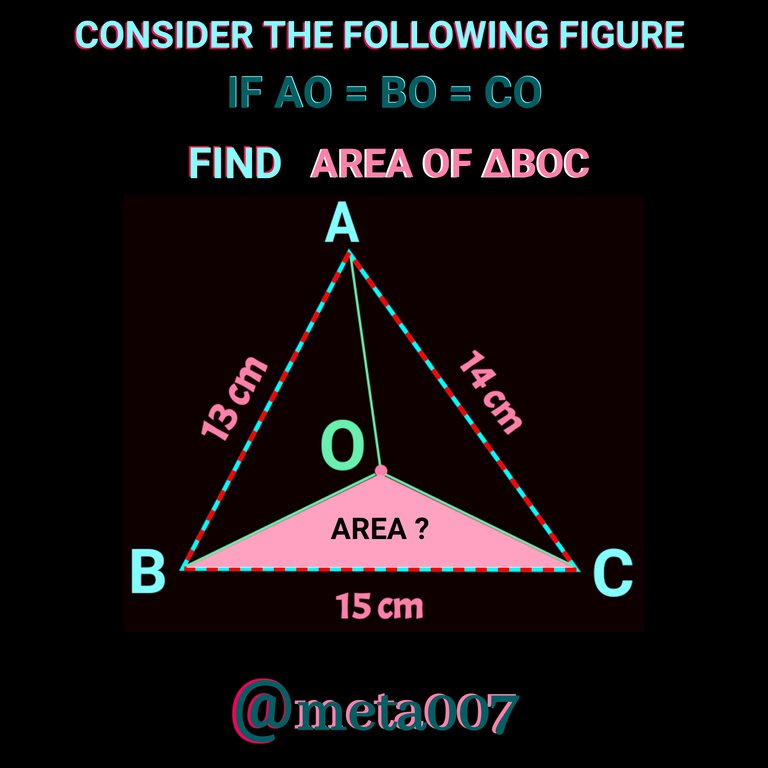
We know that area of a triangle can be given by:
(∆) = 1/2 × Base × Height
In the problem figure the height of ∆BOC is not visible but base 15 cm is given. So we need to find the height. If we draw a perpendicular from centre O to the side BC, it will be the height of the ∆BOC. Thus we will get two similiar right angle triangle but in each case we just know about one side.
We also need to find out Cir-cum-radius. So if we get the value of Cir-cum-radius(R), problem will be solve. To find out R we gonna use the following formula.
R = (abc)/(4∆)
Here, R = Cir-cum-radius.
a,b & c are the three sides of ∆ABC
∆ prepresents the area of ∆ABC.
To find out area we gonna use Heron's Formula
Actually the area of ∆ABC is crammed. It is 84 cm²
Let's compute it in the following figure:

If you wanna know derivation of above formula , hot a comment below , I'll bring it for you in next post.
Now let's draw the perpendicular OD on BC. Here OD will divide BC into two equal half as ∆BOC is a isosceles Triangle where BO = CO = R. Let's check the following figure:

In the above figure from ∆BOD:
BO² = OD² + BD²
Or, (65/8)² = OD²+ (15/2)²
Or, OD² = (65/8)² - (15/2)²
Or, OD² = (65/8+15/2 )(65/8-15/2)
[ As,a²-b² = (a+b)(a-b)]
Or, OD² = 125/8 × 5/8
Or, OD = 25/8 [cm]
Now we got the height of ∆BOC and the base is already given. So, area of the ∆BOC can be found using basic formula as follows:

I hope you liked the solution. Thanks you so much for visiting .
📢 All the figures used here are made by me only. There may be some silly mistakes, specially in figures. Try just considering data only.
Thank you so much for visiting.
Have a nice day
All is well
Regards: @meta007


