Hello maths bugs(🐞) and hivers(🐝)
I hope you are string and stout & doing good in life.
Today, I have another interesting problem bases on wuadrilateral when two sides are parallel. You Can see in the folowing picture that the trapezium has four sides measuring AB = 2cm, BC = 7cm, CD = 3cm and AD = 4cm and here side AD and BC are parallel to each other.You need to find out the area of the trapezium ABCD.
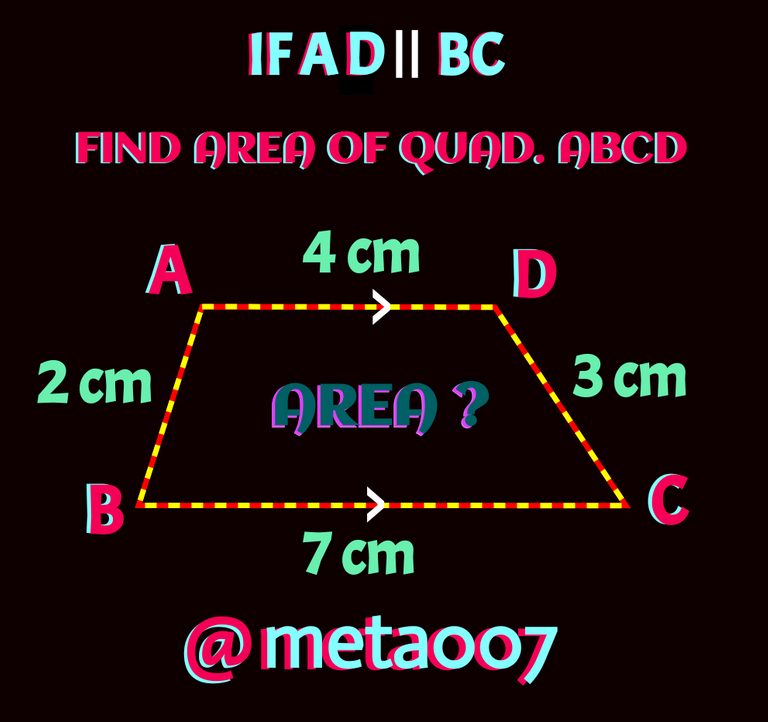
To solve it, you just need to know how to find atea of a triangle and the rest is very easy. Before heading towards the solution, please give it a try first.
Construction:
Let E be a point on BC so that AD=BE
Now, ED and AE are drawn.
Check it in the following figure.
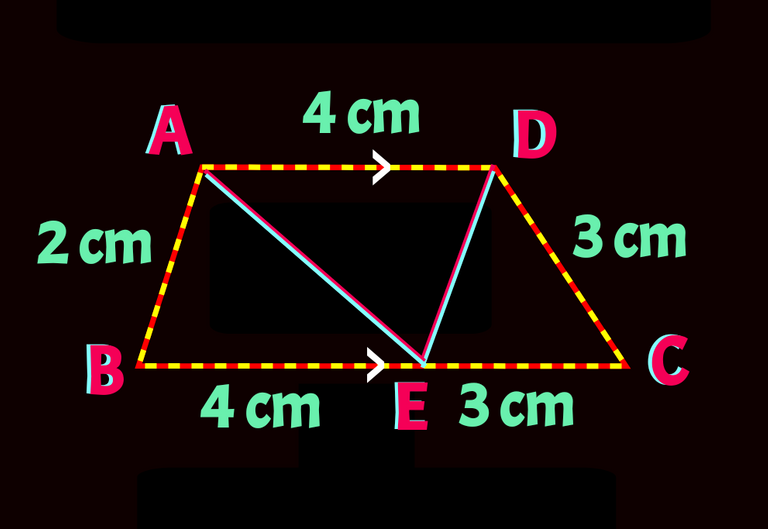
We need to find area of the three triangle shown above or parallelogram ABED and ∆CED or trapezium ABCD but we don't know the distance between parallel sides. So We are going to calculate the area of ∆CED first using Heron's triangle formulla of area.
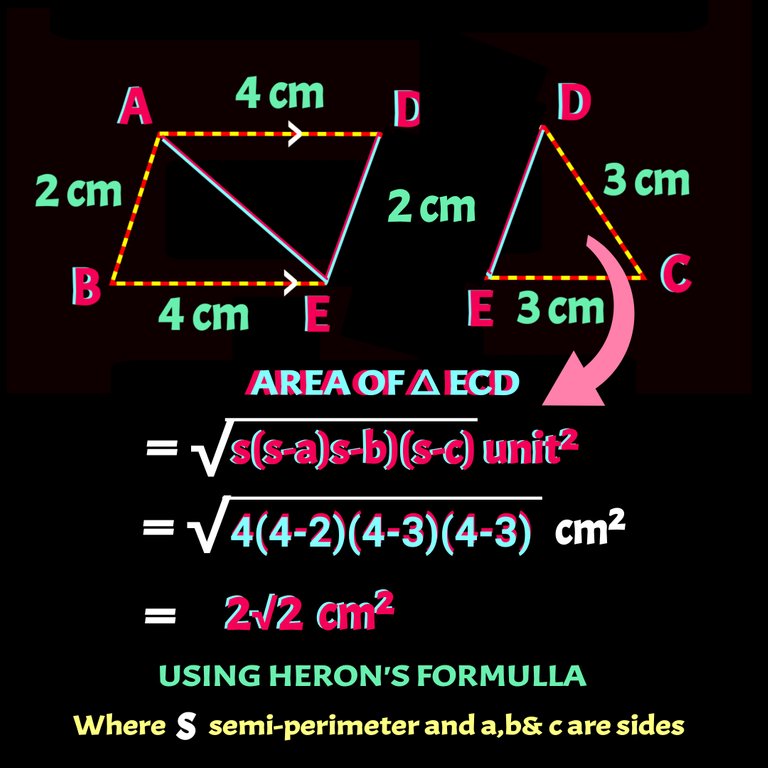
As, AD = BE and AD parallel to BE, AB will also be parallel to DE and hence DE becomes 2 cm also. Now We have to find out area of the ∆ CED first Check it the following figure.
Now, We need to find the height of ∆CED and we can find it from the equation shown in the figure below 👇
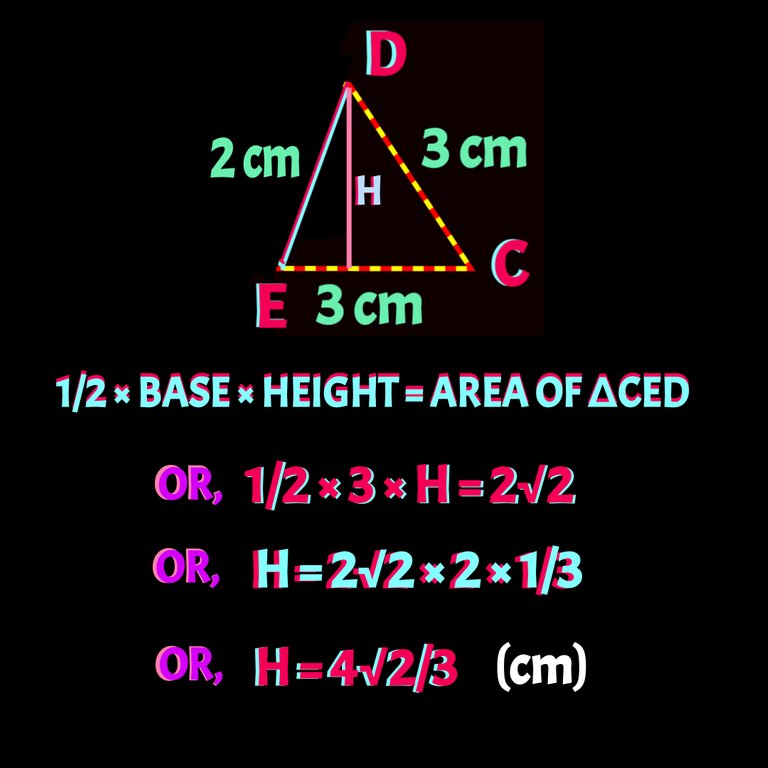
As here heinght of the ∆CED and parallelogram ABED is equal, we can find ABED's area easily. That is equal to BASE × HEIGHT = 4 × 4√2/3 cm² =16√2/3 cm² and then Aif we add area of the parallelogram and ∆CED , we can find area of the trapezium ABCD.
Or, We can now use formulla of area of trapezium as height is obtained. Check it below 👇
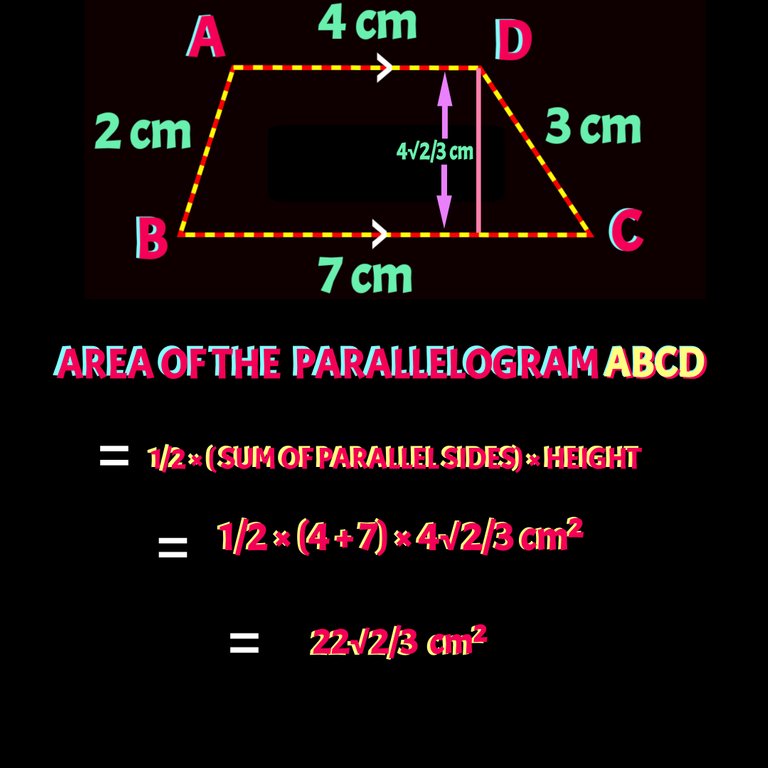
I hope you liked the problem and its solution. You want to know proof of area of triangle and heron's formulla, please a comment below, I will bring it for you.
We can find the solution just finding area of the three triangles formed after joining line segment AE and ED and for ∆ ABE or ∆ AED the base is 4 cm and the height is the dame as for ∆ CED
📢📢 All the figures used here are made by me using android application. There may be some silly mistake, please avoid them if you can.
Thank you so much for stoping by
Have a nice day
All is well
Regards: @meta007




