Hello math bugs(🐞) and hivers(🐝)
I hope you are strong and stout & doing well in life.
Well come to another interesting geometric proof. We all know about Heron's formula used to find area of a triangle when three sides of it are given. I'll show you today how to drive it.

To prove it we need to know formula of Pythagoras and to do a little construction. At first, let's draw a perpendicular from a vertex to its opposite side of the ∆"ABC*. Here I draw AD which os perpendicular to BC. Suppose, the three sides a, b , c are opposite to the respective angles A, angle B and angle C and also BD= x and CD= (a-x). Check details in the following figure:

Now we gonna use Pythagoras' formula in each of the smaller triangle namely ∆ABD and ∆ACD. In case ∆ABD , we can say c² = x² + h² or h² = c² - x². Check the follwoing figure also:
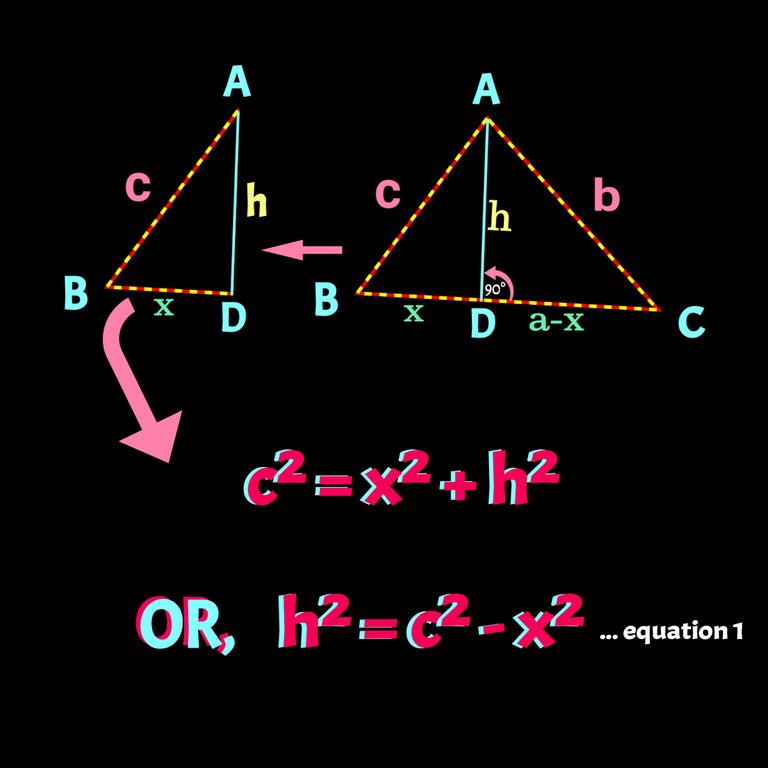
From ∆ACD , we also can get b² = (a-x)² + h² or h² = b² - a² -x² + 2ax. Check it below:
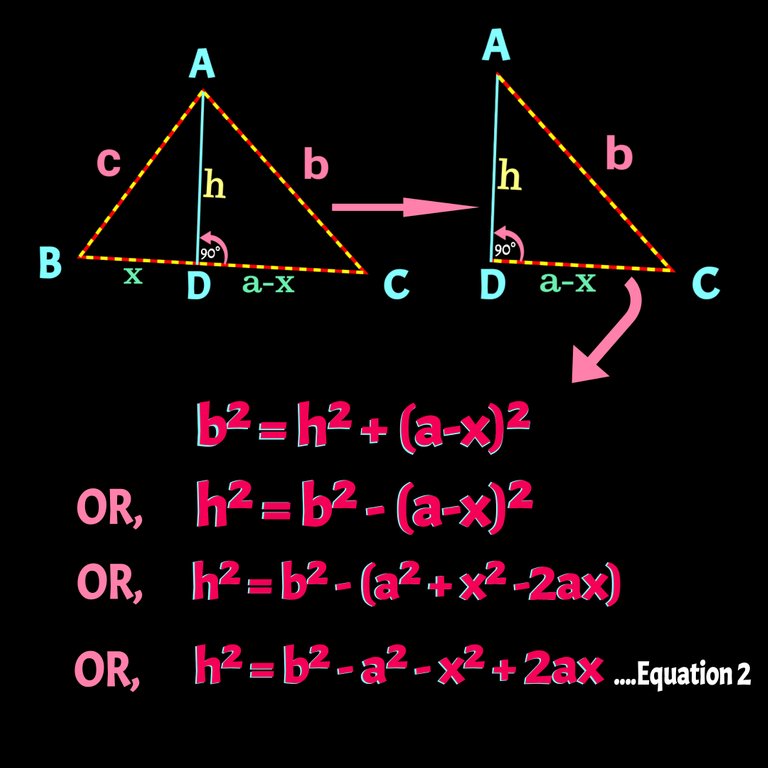
Check Heron's formula carefully. As there is no x or h in it. The the formula is given by a, b and c only. To get rid of h we need to compare equation1 and equation2 and we can have the value of x. Check the following figure:

See, our moto is to get rid other variables except a, b, and c. What can we do now! If we replace the value of x in equation1 or 2, we will have an equation devoid of unwanted variables. As equation1 is simplier than equation2, we gonna use the former. Check the figure below:
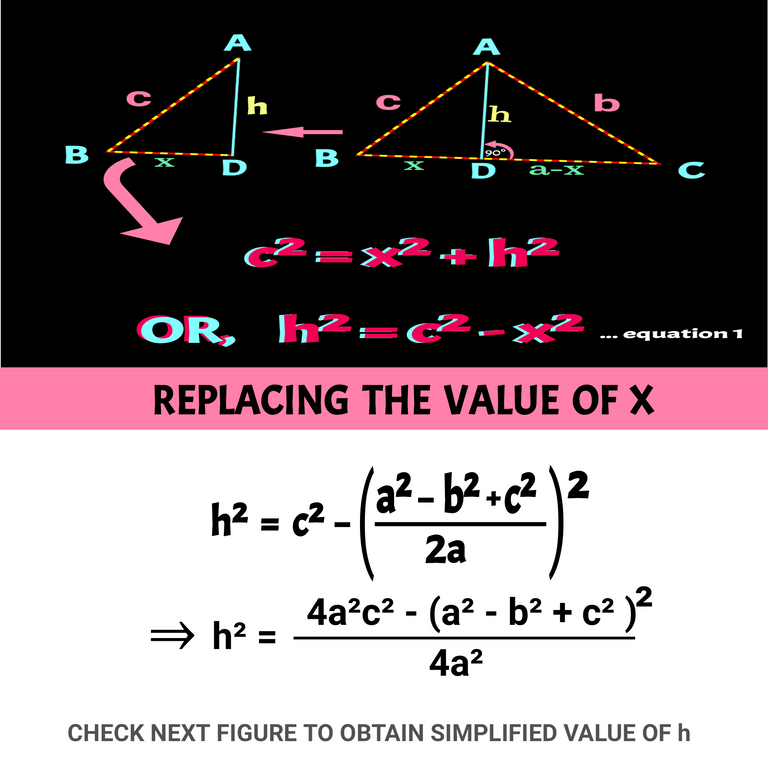
We know the area of a triangle is given by 1/2 ×base × height. Here we have consider a as base and height h. Once we find vaule of h from above equation, problem is solved because the vaule of h we gonna obtained will be in terms of three sides( a,b & c) of the ∆ABC. let's get it done.

Now area will be 1/2× base × height =1/2× a×√(S(S-a)(S-b)(S-c) unit². Also check the following figure:

All the figures and images are made by me using android application.
Please ignore the silly mistake(s) of there is any. All the figures you have seen take huge time to build. So re-editing hurts.
I hope you find this post interesting ans effortful. Thank you so much for visiting.
Have a good day.
All is well.
Regards: @meta007




