Greetings everyone! In my previous post, we have studied both 2D and 3D box and with that we have completed our particle in a box topic. We learnt to calculate the energies and wavefunction values for all these particle in a box dimensions. Today, we will see another interesting topic called as zero point energy (ZPE).

ZPE is a fascinating concept in quantum mechanics. It simply states that even in a vacuum, particles exhibit a residual energy, known as zero-point energy, which arises due to the inherent uncertainty principle of quantum mechanics. This energy has profound implications in various fields, from cosmology to nanotechnology. I will discuss the ZPE of 1D, 2D and 3D box.
ZPE of 1D Box
We have studied particle in a 1D box. Now, consider the same phenomenon as a free particle moving in an infinitely deep potential well. In this 1D scenario, according to quantum mechanics, the particle's energy cannot be zero even at absolute zero temperature due to its quantum fluctuations. This residual energy, known as zero-point energy, results as a consequence of the particle's wave-like nature.

Interestingly, the zero-point energy in a 1D box is proportional to the inverse square of the box's length, implying that as the confinement increases, the zero-point energy becomes more significant.
ZPE of 2D Box
Extending our exploration to two dimensions, we consider a particle confined within a two-dimensional square well. In this case, the particle is restricted to move within a plane. Similar to the 1D case that we have previously studied, the uncertainty principle dictates that the particle cannot come to a complete rest, even at absolute zero temperature.
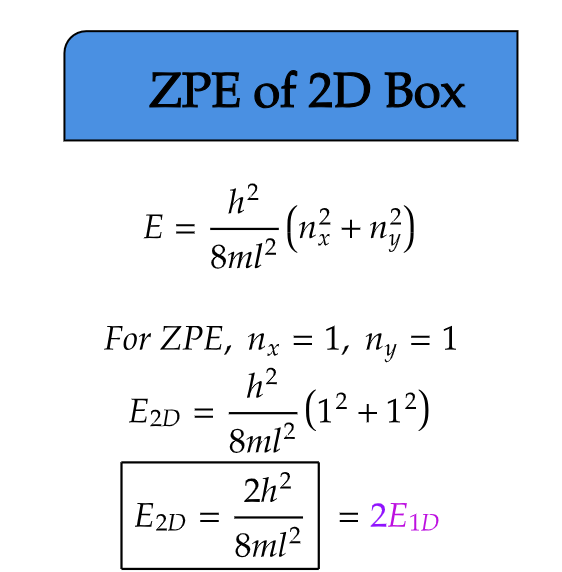
From the equation above we can see, the zero-point energy in a 2D box is dependent on the inverse of the area of the box. Notably, the zero-point energy increases as the size of the box decreases, highlighting the significance of confinement effects in two dimensions.
ZPE of 3D Box
Expanding our investigation into three dimensions, we now examine a particle confined within a three-dimensional cubic box. Here, the particle is confined within all three spatial dimensions, resulting in a richer energy landscape.
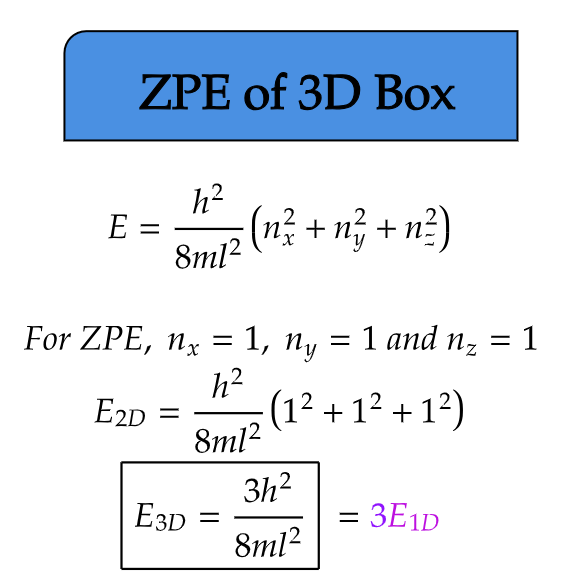
In a 3D box, the zero-point energy is determined by the inverse of the volume of the box. As the particle explores a larger space, its zero-point energy diminishes compared to the 1D and 2D cases. However, similar to the previous scenarios, the particle still retains a non-zero energy even at absolute zero temperature.
From the discussions above, we can come to a conclusion that we can arrange all these ZPEs of 1D, 2D and 3D box in a decreasing manner and the result comes out to be-

Problem) The π electrons in cyclobutadiene molecule behaves as particle in a 2D square box.
i) What will be the energy gap between highest occupied and lowest occupied energy levels in terms of h2/8ml2?
ii) What will be the total ground state energy?
Solution
We know the structure of cyclobutadiene, the name itself indicates that there are two double bonds in a cyclic manner with 4 carbon atoms.
For every π bond there are 2 π electrons. So, for 2 π bonds there are a total of 4 π electrons.
Now, let us fill these 4 π electrons in a energy level diagram.
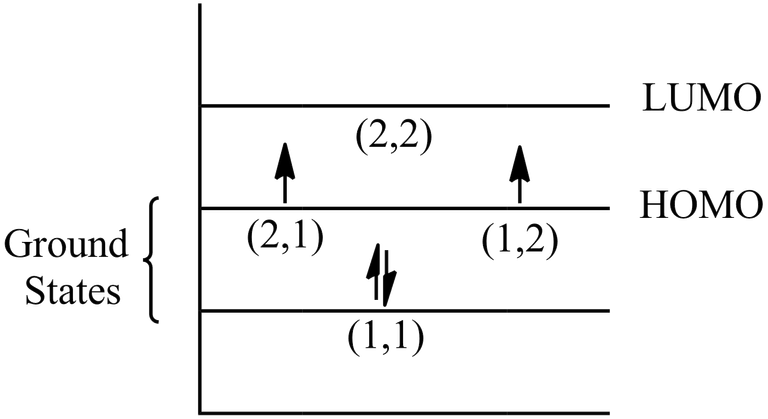
i) To find the energy for highest occupied and lowest unoccupied energy levels, we need to first find both highest and lowest energy levels corresponding to their quantum energy states.


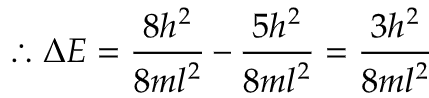
ii) Here, in question particle means π electrons and their are 4 π electrons in cyclobutadiene. Now, 2 paired electrons are present (1,1) energy state and an unpaired electron is present in (2,1) and (2,2) each state.
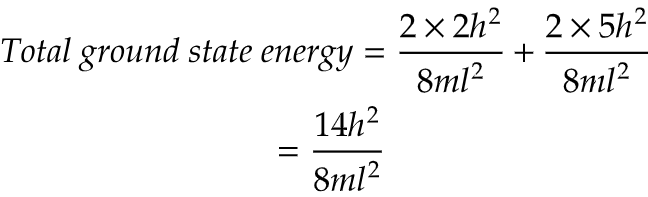
What we learnt?
We studied the basics of Zero point energy and studied the ZPE of all three cases for particle in a box case.
We arranged the energy difference of ZPE of 1D, 2D and 3D particle in a box cases.
Software used:
The mathematical equations are prepared using mathcha.io editor and diagrams are drawn using ChemDraw software.

If you like my work and would like to support me, you can do so by joining my fanbase by clicking this link
Quantum Confinement : Particle in a 2D box and 3D box | ChemFam #83 |
Molecular Chirality: A Mirror Image Perspective | ChemFam #82|
Exploring Time-Independent Schrödinger's Wave Equation and Particle in a 1D Box | ChemFam #80 |
The Role of Gamma Function in Quantum Mechanics | ChemFam #79 |
Postulates of Quantum Mechanics and Normalization of Wavefunction |ChemFam #78|
Understanding Commutator Relations and Exploring Eigenfunctions in Quantum Mechanics |ChemFam #77|
How to find Expression of an Operator and Commutation Relations |ChemFam #76|
Basics to Quantum Chemistry: Operators, Functions and Properties of Operators |ChemFam #75|
A Comprehensive Study of Euler's Reciprocal Rule in Thermodynamics |ChemFam #73|
A Deep Dive into Nutrition Essentials: Your Path to a Healthier, Happier You |ChemFam #72|
Decoding Liver Function Tests through Chemistry |ChemFam #71|
Understanding the Dynamic Roles of Metalloenzymes and Metal-Activated Enzymes |ChemFam #70|
Cracking the Thermal Code: Differential Thermal Analysis in Modern Research |ChemFam #69|
Applications and Importance of IR Spectroscopy: Shedding Light on Molecular Structures |ChemFam #68|
PS The thumbnail image is being created by me using canva.com
Games I play on Hive
| Games I play on Hive | Game description |
|---|---|
| Terracore | Terracore is an Idle mining game based on Hive blockchain |
| Rise of the Pixels | ROTP is a Web3 browser game about game development on Hive |





