Greetings to everyone! In the previous blog on the ongoing series on quantum mechanics we have studied about significance of wavefunction and wavefunction plots for 1D box. Today, we shall study the 2D and 3D box and will see how to find out the wavefunction and energy values. How we can apply the same concept from the 1D box and derive the equations for 2D and 3D box.

Particle in a 2D Box
Imagine a particle, such as an electron, confined within a two-dimensional box, having length lx and ly in x and y direction. According to the principles of quantum mechanics, the particle's wave function is quantized within the box, leading to discrete energy levels. The Schrödinger equation governs this system, providing a mathematical framework to describe the particle's behavior.
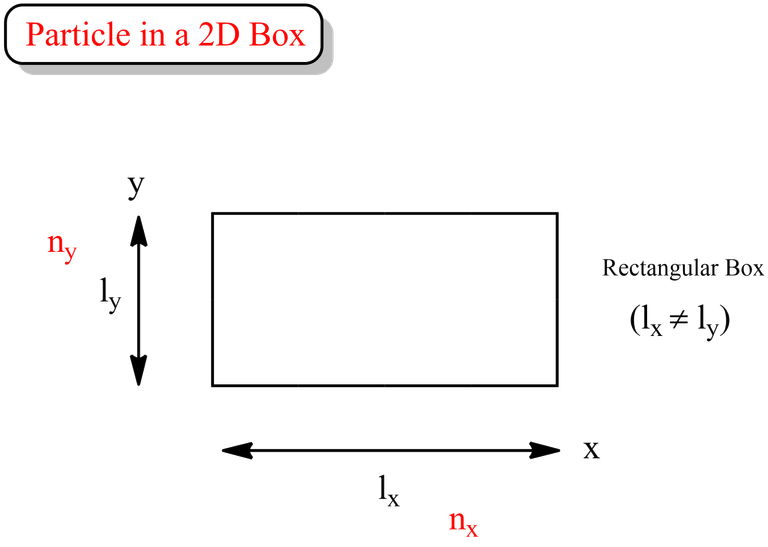
If we are to derive expression for wavefunction of the said particle in that 2D box, then we can do that by applying the same concept that we have learnt in the case for 1D box. Your forgot? No worries, I've got you.
We have also studied that wavefunctions are multiplicative in nature. So we can multiply the wavefunctions for both x, i.e., Ψ(x) and y direction i.e., Ψ(y) to find out the Ψ(x,y).
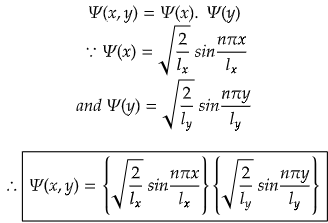
Now, we also know from previous studies that energy is additive in nature. So, from the energies of E(x) and E(y), we an find out the energy E(x,y) by simple addition.

And for a square box, we get the above expression for wavefunction.
Mostly, we assume particle in a square 2D box, when the question only mentions particle in a 2D box. If it is not mentioned in the question whether the box is rectangular or a squared one, it is always preferential to go with a square box.
Particle in a 3D Box
Extending our exploration to three dimensions, we consider a particle confined within a cubic box. The additional dimension introduces new complexities and nuances to the quantum behavior of the system. Similar to the 2D case, the particle's wave function becomes quantized, resulting in discrete energy levels determined by the box's dimensions.
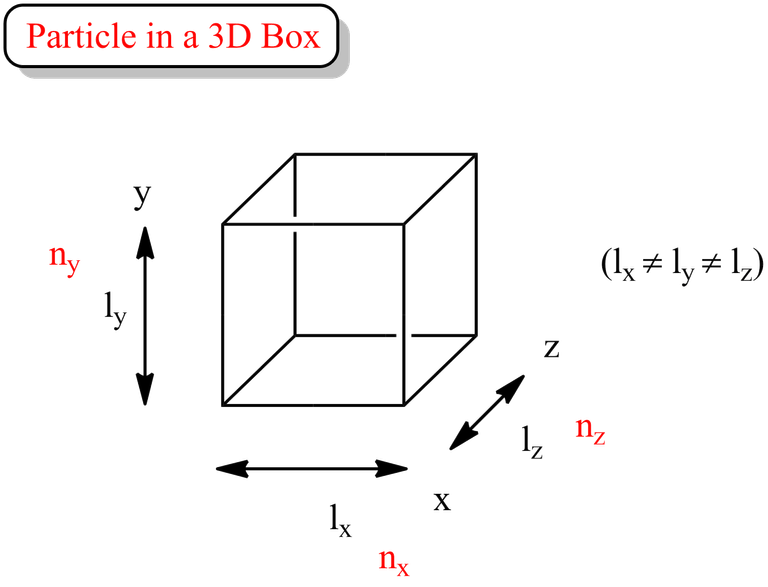
Now, let us see the expressions for wavefunction and energy values for a 3D box. As mentioned earlier wavefunction is multiplicative in nature and energy is additive in nature.

We have seen the expression when the box is a cube of same length. In a 3D box, the quantum states become even more intricate due to the increased degrees of freedom. The particle's wave functions exhibit more complex spatial patterns, involving combinations of multiple quantum numbers. The energy levels in a 3D box are higher in number compared to a 2D box, reflecting the increased spatial freedom.
What we learnt?
We studied the expression for wavefunction and energy for particle in a 1D box. We have applied our concepts on wavefunction's multiplicative nature and energy's additive nature to derive the said expressions.
We studied particle in a 3D box. We saw how the addition of one more dimension affects the expressions. We also checked, how it goes for a cube.
Software used:
The mathematical equations are prepared using mathcha.io editor and diagrams are drawn using ChemDraw software.

If you like my work and would like to support me, you can do so by joining my fanbase by clicking this link
Molecular Chirality: A Mirror Image Perspective | ChemFam #82|
Exploring Time-Independent Schrödinger's Wave Equation and Particle in a 1D Box | ChemFam #80 |
The Role of Gamma Function in Quantum Mechanics | ChemFam #79 |
Postulates of Quantum Mechanics and Normalization of Wavefunction |ChemFam #78|
Understanding Commutator Relations and Exploring Eigenfunctions in Quantum Mechanics |ChemFam #77|
How to find Expression of an Operator and Commutation Relations |ChemFam #76|
Basics to Quantum Chemistry: Operators, Functions and Properties of Operators |ChemFam #75|
A Comprehensive Study of Euler's Reciprocal Rule in Thermodynamics |ChemFam #73|
A Deep Dive into Nutrition Essentials: Your Path to a Healthier, Happier You |ChemFam #72|
Decoding Liver Function Tests through Chemistry |ChemFam #71|
Understanding the Dynamic Roles of Metalloenzymes and Metal-Activated Enzymes |ChemFam #70|
Cracking the Thermal Code: Differential Thermal Analysis in Modern Research |ChemFam #69|
Applications and Importance of IR Spectroscopy: Shedding Light on Molecular Structures |ChemFam #68|
The Silent Revolution: How Polymers are Shaping Our World? |ChemFam #67|
Beyond the Bin: The Many Faces of Plastic Management |ChemFam #66|
Spectrophotometry Simplified: The Beer-Lambert Law in Spectrophotometry |ChemFam #65|
Chromatography: Unraveling the Science of Separation |ChemFam #64|
Colorful Clues: The Magical World of Chemical Indicators |ChemFam #63|
Colloids in Action: Impacting Your Daily Life More Than You Think |ChemFam #62|
The Complex Landscape of Opioid Analgesics: Addressing The Concerns |ChemFam #61|
Genetic Engineering: Pioneering Progress or Ethical Predicament? |ChemFam #60|
The Guardians Against Microbial Menace: Antibacterial Agents |ChemFam #59|
The Cholesterol Conundrum: The Story of Statins |ChemFam #58|
PS The thumbnail image is being created by me using canva.com and a template Image by WangXiNa on Freepik
Games I play on Hive
| Games I play on Hive | Game description |
|---|---|
| Terracore | Terracore is an Idle mining game based on Hive blockchain |
| Rise of the Pixels | ROTP is a Web3 browser game about game development on Hive |









