Greetings everyone! In my last post, we have completed the degeneracy topic. For that, we have covered all three cases of particle in a box. After the particle in a box type cases, let us move onto a next system. A system showing quantization of vibrational motion. We shall be discussing about the simple harmonic oscillator (SHO).

In quantum mechanics, harmonic oscillators are an important paradigm because they provide models for a variety of systems, such as electrodynamic field modes (photons) and vibrations of molecules and solids (phonons).
Quantum harmonic oscillators are important for two reasons. First, it's a quantitatively useful model for just about every little thing that moves. Examples include vibrations of molecules and acoustic vibrations (phonons) of solids. Simple harmonic oscillators also serve as a basis for modeling the oscillations of electromagnetic fields and other fundamental quantum fields in nature. Second, simple harmonic oscillators are another example of a one-dimensional quantum problem that can be solved precisely. The detailed solution provides additional insight into the behavior of general quantum systems, helping us understand which features of infinite square wells are and are not common to all trapped quantum particles.
The Classical Harmonic Oscillator
Vibrations occur throughout nature, including electromagnetic waves, vibrating molecules, and tree branches gently swaying back and forth. Newtonian mechanics studies the macroscopic oscillations of spring-loaded blocks and simple pendulums. Consider the case of a block on a spring. In this section we consider only one dimension of vibration. Assume the mass moves back and forth along the x direction about the equilibrium position x = 0.
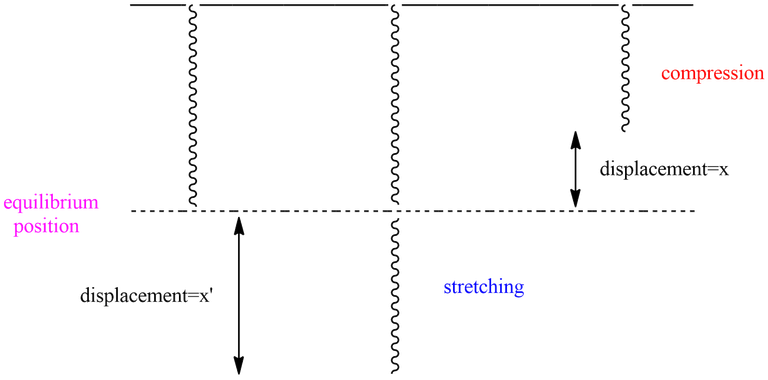
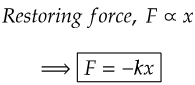
In classical mechanics, particles move under the action of a linear restoring force, defined by the expression F=−kx. Where x is the displacement of the particle from its equilibrium position. Movement occurs between two turning points x±A. Here A represents the amplitude of movement.
The Quantum Simple Harmonic Oscillator
One of the problems with this classical formula is that it is not general. For example, it cannot be used to describe the vibrations of diatomic molecules, where quantum effects are important.
From, Newton's Law of Motion in regards with the classical condition,
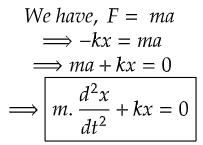
It was experimentally found that the solution to the above equation is,
x=A sin(2π𝛎t), where A is amplitude, 𝛎 is vibrational frequency and t is time. The position of the object varies periodically in time with the vibrational frequency.

Now, if we put this value on the equation following the classical condition, then we will be able to find the vibrational frequency of the particle.
So, putting this value in the equation involving classical condition,

Here, k is called as the force constant which represents bond strength, m is mass of the particle. It is worth mentioning here that for diatomic (A-B) molecule, we tale m=reduced mass (μ).
Potential Energy
We can define the potential energy again from classical conditions,

Here, x is the displacement, k is force constant and V is potential energy.
This potential energy function describes the restoring force acting on the particle, which is directly proportional to its displacement from equilibrium.
Quick Recap
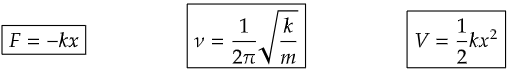
Total Energy of SHO
We can find out the total energy of the SHO by simply adding both kinetic and potential energy of the oscillator.
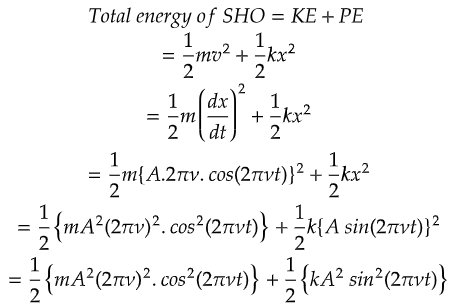
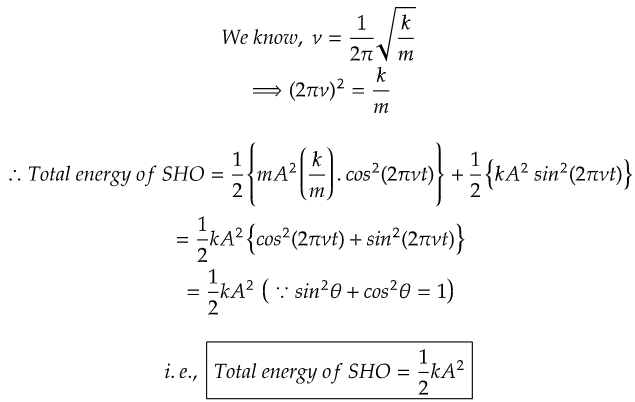
It can be seen and conferred that the total energy of SHO depends on force constant and amplitude.
What we learnt?
We studied what harmonic oscillators are and discussed why they are so important in quantum as well as classical mechanics.
We discussed that the simple harmonic oscillator in quantum mechanics exhibits a distinct interplay between its kinetic and potential energies. The kinetic energy arises from the particle's motion within the potential well, while the potential energy stems from the restoring force associated with the oscillator's displacement from equilibrium.
The total energy of the SHO is the sum of the potential and kinetic energy components. We saw that it depends on the force constant, k and amplitude, A.
Software used:
The mathematical equations are prepared using mathcha.io editor and diagrams are drawn using ChemDraw software.

If you like my work and would like to support me, you can do so by joining my fanbase by clicking this link
Understanding Degeneracy in Quantum Chemistry: Exploring 1D, 2D and 3D Box Models | ChemFam #85 |
Introduction to Zero Point Energy and its Cases in Particle in a Box | ChemFam #84 |
Quantum Confinement : Particle in a 2D box and 3D box | ChemFam #83 |
Molecular Chirality: A Mirror Image Perspective | ChemFam #82|
Exploring Time-Independent Schrödinger's Wave Equation and Particle in a 1D Box | ChemFam #80 |
The Role of Gamma Function in Quantum Mechanics | ChemFam #79 |
Postulates of Quantum Mechanics and Normalization of Wavefunction |ChemFam #78|
Understanding Commutator Relations and Exploring Eigenfunctions in Quantum Mechanics |ChemFam #77|
How to find Expression of an Operator and Commutation Relations |ChemFam #76|
Basics to Quantum Chemistry: Operators, Functions and Properties of Operators |ChemFam #75|
A Comprehensive Study of Euler's Reciprocal Rule in Thermodynamics |ChemFam #73|
A Deep Dive into Nutrition Essentials: Your Path to a Healthier, Happier You |ChemFam #72|
Decoding Liver Function Tests through Chemistry |ChemFam #71|
Understanding the Dynamic Roles of Metalloenzymes and Metal-Activated Enzymes |ChemFam #70|
Cracking the Thermal Code: Differential Thermal Analysis in Modern Research |ChemFam #69|
Applications and Importance of IR Spectroscopy: Shedding Light on Molecular Structures |ChemFam #68|
PS The thumbnail image is being created by me using canva.com
Games I play on Hive
| Games I play on Hive | Game description |
|---|---|
| Terracore | Terracore is an Idle mining game based on Hive blockchain |
| Rise of the Pixels | ROTP is a Web3 browser game about game development on Hive |




