Back in the 1600s while Newton was experimenting with white light he first discovered that it can be separated into different colors, he used a prism to do that and realized that the white light was just a composition of lights from all colors, it was later understood that light was a spectrum of wavelengths, compromised of not only the portion that we can see but it ranges from 1000s millimeters to a picometre (1×10^-12 of a meter) in wavelength.
Newton thought light gets emitted from a source in large numbers of tiny particles which was called then "corpuscles". And his findings were partially correct, we call the particles of light now "photons" which comes from the greek word (phōs) for light.
We can know Newton was correct and they are indeed particles because we can measure them with a very sensitive device called the "photomultiplier".[1] It's a device that can convert the incident photon into an electric signal.
And we can even detect a single photon with it in a simple way.
Photomultiplier
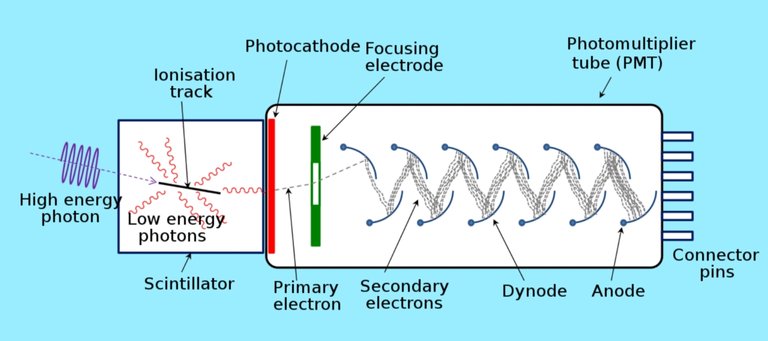
A photon hits the first plate, knocking off a single electron which gets attracted to the second plate, hitting it and knocking off few electrons, and those in turn fly off to the third plate, each knocking off few electrons ending up with more electrons being knocked off at each step and so on, the number of the electrons knocked off multiplies exponentially until we have a very large number of electrons at the final plate, enough to produce an electrical charge that can then be amplified even further with an amplifier, ending up with a "click" registered each time a single photon hits that first plate.[1]
We get "clicks" when we shine a beam of light on it, getting many clicks when the beam is bright but fewer clicks as the beam gets dimmer, until it's very dim and we get a click every once in a while.
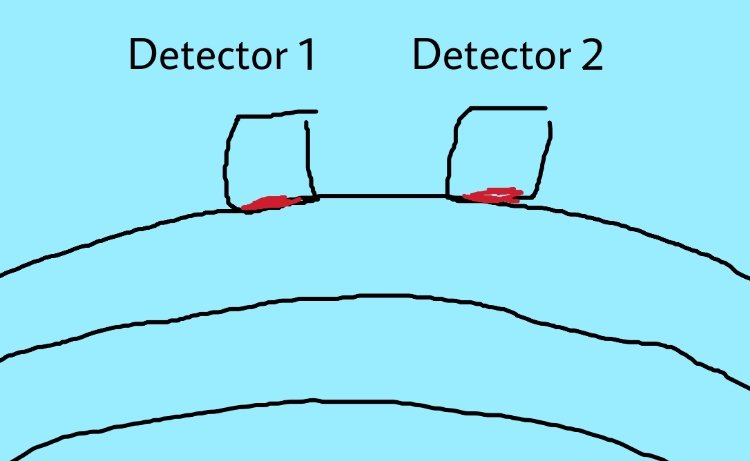
Placing two photomultipliers next to each other, one of them only goes off at a time per instance photon, never both at the same time which is what can be expected to happen if the photon was a wave (a wave would cause both to go off).
Those clicks and effectively those particles of light come in the form of raindrops. They are particles in every way and we can even count them. Bright light, more "clicks" per second, dim light less "clicks" per second. Each of those particles is the same and most importantly there's no "half" particle.
(Note: whenever I mention light in the examples, I'm talking about monochromatic light, that is, light of a single wavelength)

Partial Reflection Weirdness:
If you look through glass or water you can see through it but you can also see some reflection. Apart from the fact that reflections can be beautiful, we can also notice about that some of the light seems to go through the glass, but some of it goes back.
If a beam of light heading straight down towards glass for example, only about 4% of the light reflects.
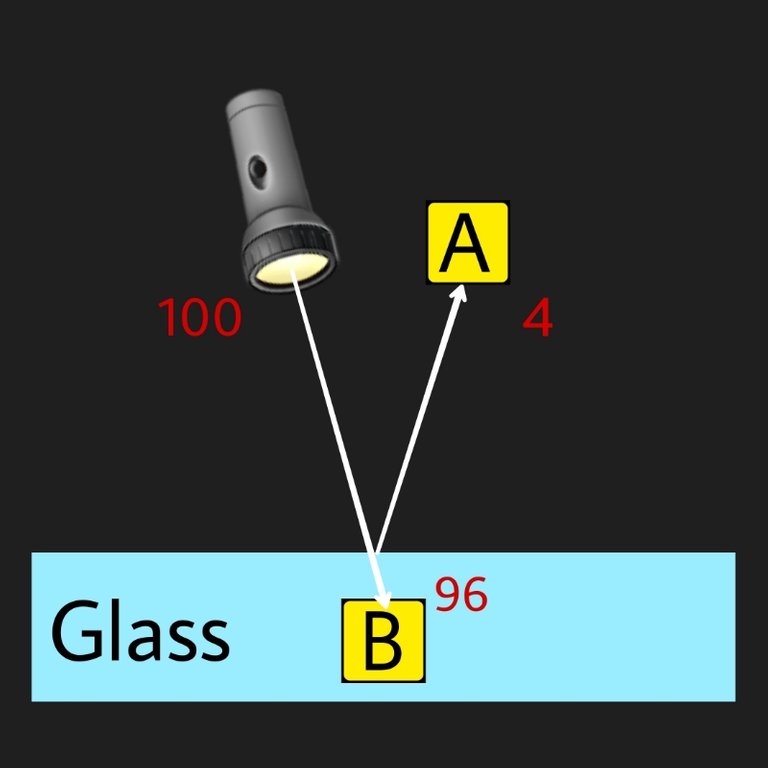
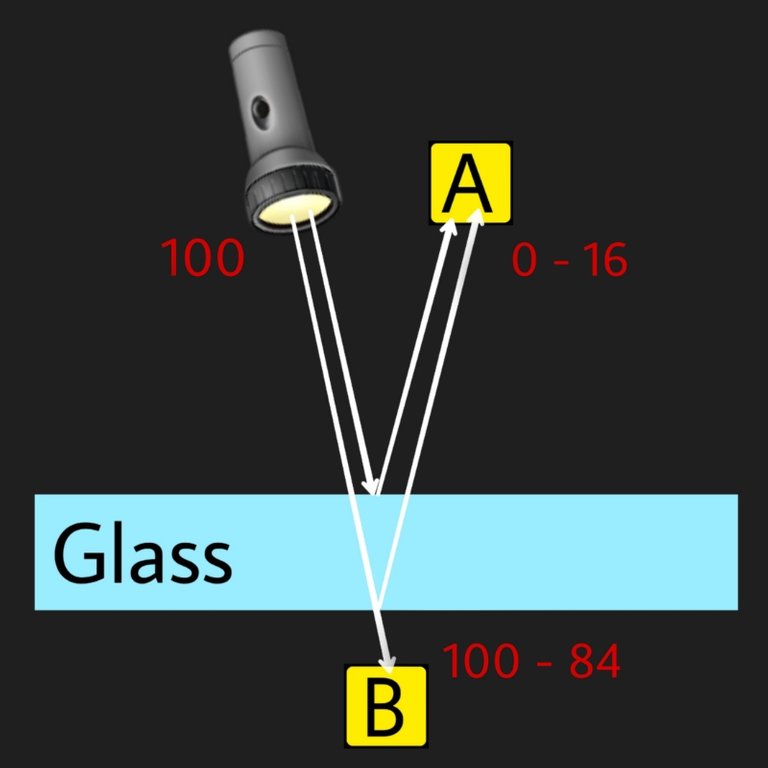
What's intriguing and amazing about this is that say we send a 100 photon on the surface of glass, we place a photomultiplier above the glass (A) and another inside of it (B) to count how many gets reflected out of those and how many make it through, we find that on average 4 photons get reflected and 96 make it through.
The puzzling thing about this is, if they are particles what determines WHICH photons get reflected ?
The phenomena seem to be probabilistic, nothing determines it. Pure chance! Each particle has the same chance of that 4% (in our glass example) getting reflected.
Just like the odds if you have a die and you want to roll a 1, it won't happen so often but you will roll a 1 from time to time it's a 1/6 chance!
Roll it 600 times and you should get close to around a hundred 1s.
To make things even more mind boggling, if we move the second photomultiplier below the glass instead of inside it, effectively having now 2 surfaces to that glass. Photons can now get reflected either by the front surface or the back surface of that sheet of glass.
Intuitively, we would think that if a particle which had 4% chance to reflect off one surface, would now have another 4% chance reflecting off the second surface too, adding up to an 8% chance.
Well, nature seems to be much more counterintuitive in that case.
Depending on the thickness of the glass, we start with 0% reflection when it's super thin (can think as if there is no glass there). Then the reflection increases as the glass sheet gets thicker, 1% .. 4% .. 8% but keeps going all the way up to 16% (twice what would be expected).
But then something REALLY strange happens.
As we increase the thickness of the glass sheet further that 16% starts dropping again, keep making the glass thicker and the reflection drops back to 0% at some point, just to start going up AGAIN as we keep gradually increasing the thickness.
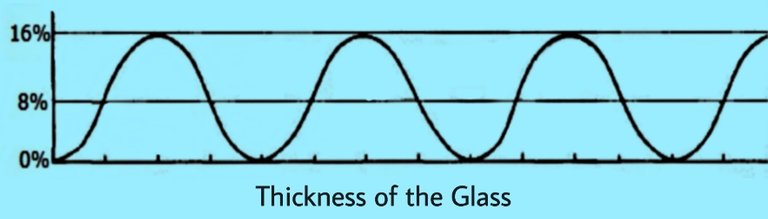
And that pattern is infinite! No matter how much we keep increasing the thickness, the exact same pattern keeps repeating over and over again. From no reflection to 16% reflection, back to 0%, and so on...

Probability amplitudes simplified:
In quantum electrodynamics we can explain HOW that happens and how we can calculate probabilities. The "WHY does nature behave that way?" question, is not something that really can be answered (so far at least).
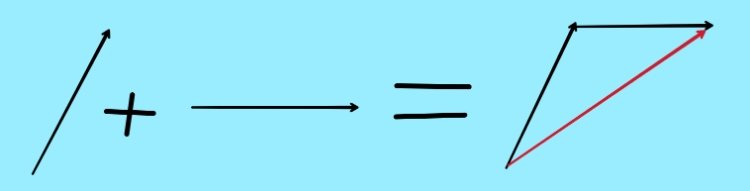
Not that physicists spend their time drawing millions of arrows, but the basic idea behind their very complicated calculations can come down to this. Drawing arrows!
Imagine you have an old style stopwatch, the one with an arrow that spins, and you start it the moment you send a photon towards the glass, then you stop it as soon as the photon hits the photomultiplier we placed above. The arrow would end up pointing in some direction. Let's say this photon reflected off the front surface, and the arrow of the stopwatch ended up pointing at the 30 seconds mark (after many rotations).
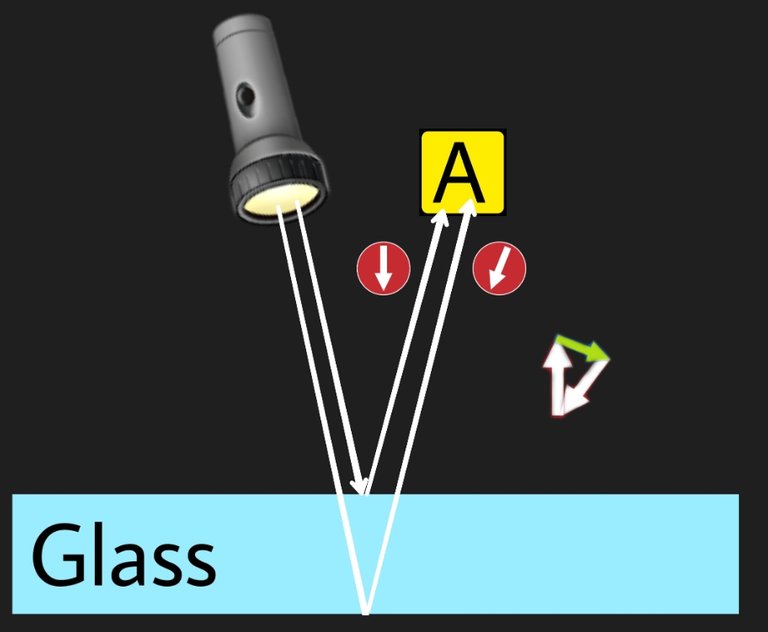
A second photon that reflects off the back surface, would have to travel a longer distance, ending up taking a little bit more time on our stopwatch, let's say our stopwatch arrow would point at the 35 seconds mark.
To calculate the probability, we simply add the arrows! (After flipping the direction of the air to air reflection arrow) This is done by placing the start of one arrow at the end of the other arrow while retaining their directions.
Then drawing a new arrow from the beginning of the first one to the end of the last one. (The green arrow in the illustration above).
The probability would be the square of the length of that final arrow.
For every event, we draw an arrow for each way that event can happen, add all the arrows together to get the final arrow.
In our example of the glass the lengths of the arrows are the same, each surface can reflect about 4% of the light, so each of the arrows has 0.2 length (0.04 when squared), but the deciding factor for the probability of reflection is the orientation of the arrows we are adding.
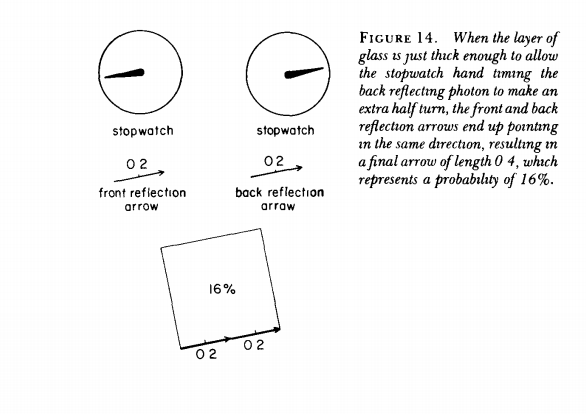
The reason we get a 0% reflection for example is when the 2 arrows point exactly at the opposite direction of each other (one stopwatch arrow points at 60, and the other at 30 for example), canceling each other out when added, ending up with 0 length final arrow, and the 16% probability is when they align in the same direction, ending up with twice the length of one arrow as the final result of the addition.
The thicker the glass gets the different timing we measure and the different orientations of the arrows we get and eventually the length of the final arrow, hence the pattern keeps repeating as we keep increasing the thickness of the glass.
In reality, it is much more complicated than this. Neither the light is getting reflected by the top surface or the back surface of the glass, nor the path of the photon is that simple. But the concept is the same, the idea of adding up the arrows of all the possible events to calculate probability amplitudes underlines the concept of QED and its complicated math, which can explain almost everything in nature.
I will try to explore more strange behavior and phenomena of light from a Feynman QED point of view in a future article now that we have explored some basics.

● Thank you for reading ●
● •