
I explored in my last post "Corpuscles of Light - QED Simplified" how single photons can be detected using a photomultiplier, and how they are indeed particles in every way.
I went on then to take a look at the strange quantum behavior of photons regarding the phenomena of partial reflection of light from glass surface and how the thickness of the glass changes the probability of the reflection in a peculiar way, going up and down from 0% to 16% indefinitely despite the glass only getting thicker.
We took a look at and explained how such probabilities can be understood and calculated using quantum mechanics in a simplified way using only spinning arrows to draw what is called the probability amplitudes. (Phase Vectors)
Today, we will explore more of the quantum behavior of photons. How photons really take all possible paths, and why we see the end result of light behaving the way we see it.
Hopefully this will give a more clear picture about one of our most successful theories in physics, Quantum Electrodynamics (QED) in a very simplified and easy to understand way.

First of all, it's worth mentioning and clarifying that QED deals with the behavior and interactions between light and matter.
The Electron among other particles with mass and a spin, has a property called "the magnetic dipole moment", just like a magnet and it's caused by its intrinsic properties of spin and electric charge. Think of it from classical electrodynamics point of view for simplification purposes, a rotating electrically charged body creates a magnetic dipole with magnetic poles of equal magnitude but opposite polarity.
This can be measured, and has been measured to an astonishingly extreme precision.
Just to give you an idea about how precise and successful QED has been. The actual experimental measurements of the anomalous electron's magnetic dipole moment has been measured to an accuracy of (7.6 parts in 1013).
This is like measuring the distance from your head to the moon with uncertainty of the measurement being from your chin or the tip of your nose!
How light really behaves:
First, here's a reminder about how we arrive at our probability amplitudes.
The probability of any event is the square of the final arrow.
And to get that final arrow, we draw an arrow for each way an event can happen, then we add them up together to arrive at the final arrow, the square of which is the probability.
Reflection:
You may have heard that light travels in a straight line, and that the angle of incidence equals the angle of reflection. This isn't entirely true, light actually travels in all possible directions and the probability of it going in any of those directions is the same.Let's say we have a mirror, with a light source at one side and a photomultiplier to detect the reflected light at the other side. In the middle we place a "wall" to prevent light from directly traveling from the source to the photomultiplier, so all light that gets detected is reflected off the surface of the mirror.
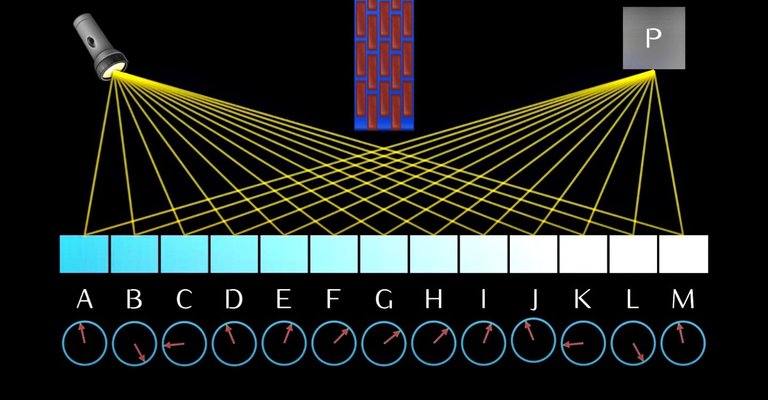
To calculate the probability of the light arriving at the photomultiplier, we take all the possible paths (should be millions of arrows and the more paths we consider the more accurate our results would be, but we draw only a few for simplicity).
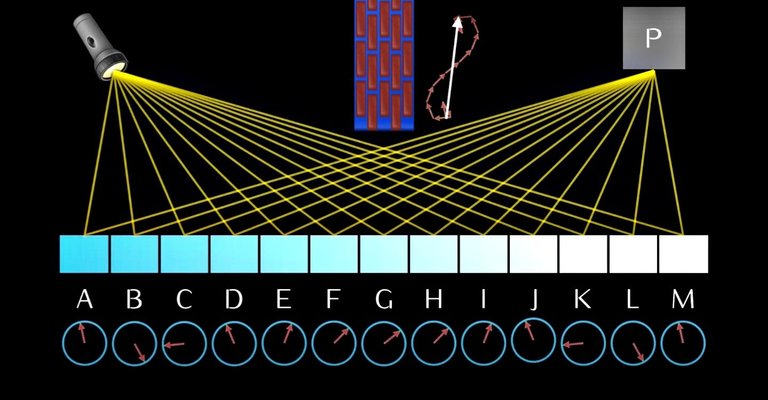
Having a stopwatch for each path, we get an arrow pointing in some direction for each path the photon takes.
Next, we add up the arrows to get the final arrow (the square of which would be the probability).
This is an awesome animated illustration from wikipedia that shows the whole process:
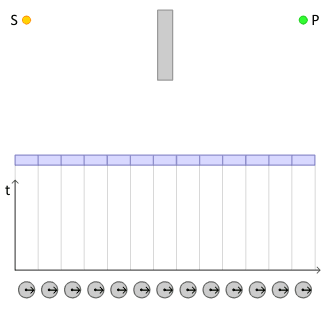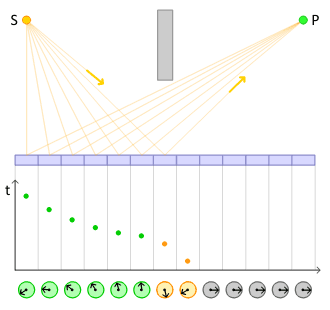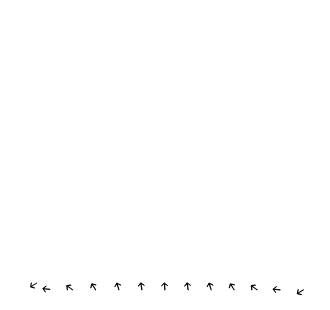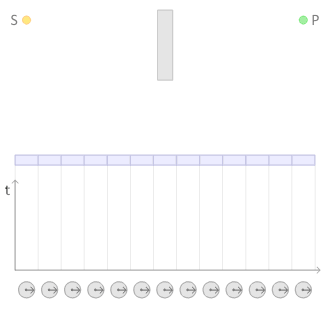
Notice how the arrows from the sides of the mirror curl up and cancel eachother, leaving mostly the pathes in the middle contributing the most to the reflection of the light.
And this is why it works to say that light reflects in the middle and the angle of the incidence equals the angle of reflection, even though in reality, all the angles and paths contribute to the reflection even though we do not directly see it.
And to prove that, we can chop off most of the mirror, leaving a piece under the light source to the side.
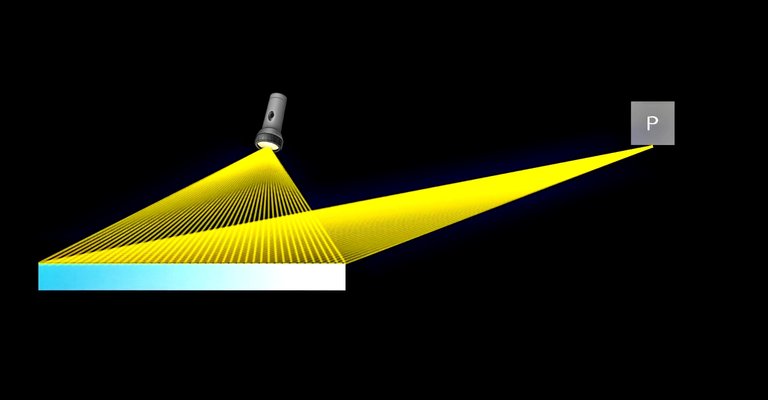
Very few light if any can reach our photomultiplier, and we can see why using our stopwatch and adding up the arrows to see the probability.
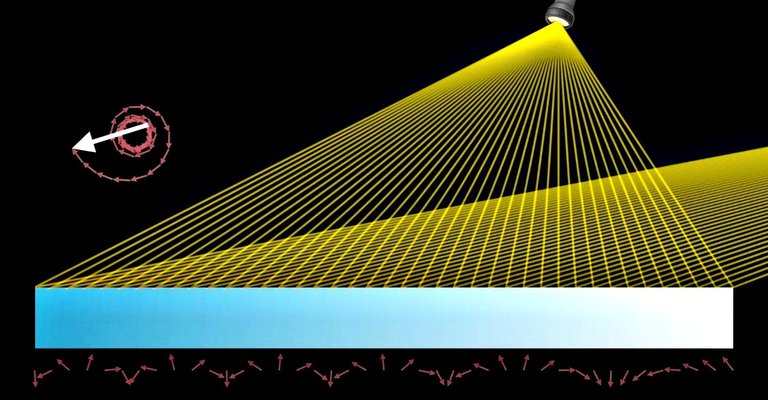
The arrows from the paths go in circles, barely adding up to anything of value for our final arrow, and as expected we wouldn't get much if any reflection towards the photomultiplier like that. But watch what happens in the next illustration if we chop off some pieces of the mirror.
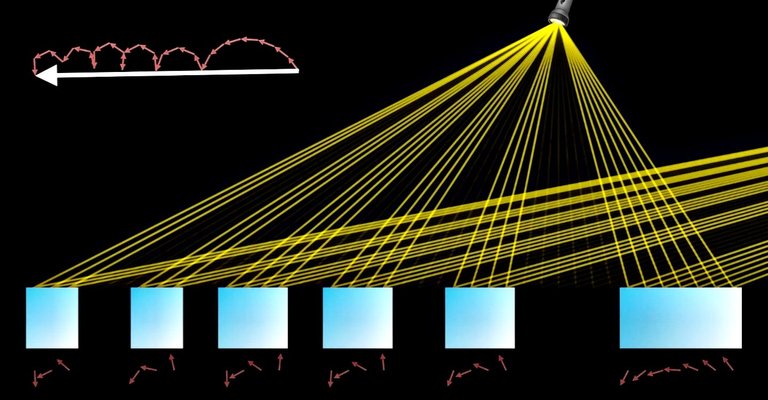
The pieces we remove from the mirror are not random as you might have figured out already, we removed slices where the probability amplitude arrows would point in the other direction which previously caused them to go in circles earlier.
This time, we prevented that from happening by removing specific pieces of the mirror, and when our arrows get added now, they make a very sizeable final arrow, and essentially a much higher probability for reflection towards our photomultiplier.
This is called Diffraction grating. And if we shine white light on that mirror instead of the monochromatic yellow light we were using, we would get different wavelengths of light reflecting at different angles.
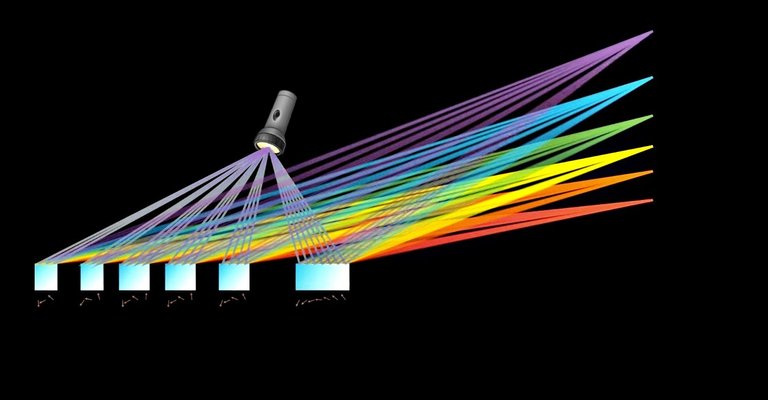
You can see this when looking at the back of a CD or DVD for example. 📀
The diffraction grating phenomena has so many applicable uses I won't get into them in here.

Refraction:

Someone under water also for example, looking up at a drone hovering above the water, would see that drone in a different place than where it actually is.
Let's take a look at this with our arrows from a QED perspective.
First, we have to know that light does travel slower in a medium like water or glass, so a straight line from the drone to the scuba diver might look as the shortest path. However, it's NOT the fastest path for light to take despite it being the shortest.

Taking all the possible paths that light could take from the drone to reach our scuba diver's eyes under the water. The fastest route the light could travel in gets reinforced with more arrows pointing in a similar direction which reinforces the probability for that route, while the other (slower paths) arrows get canceled out.
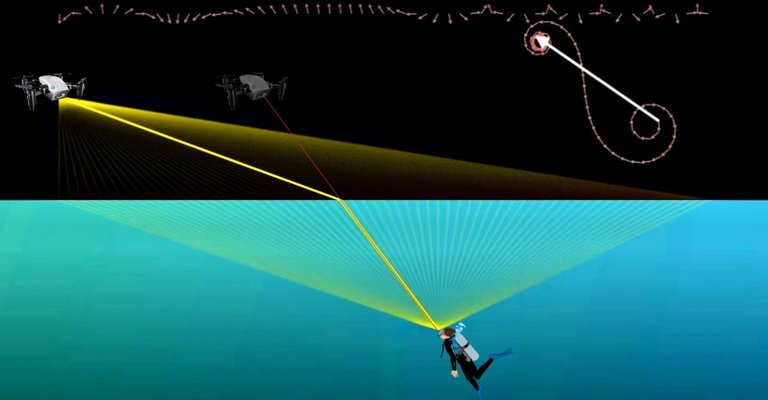
However, our senses are trained to think the light takes a direct path, making that scuba diver see the object (the drone in this case) in an imaginary position instead.

Lens:
One trick we can play on photons, which also shows how photon really takes all the paths and that all the paths it takes matters is this:
First we shine light from a source, and we detect it at the other end with a photomultiplier. The middle paths contribute the most to the probability amplitude of our final arrow and that's basically why we see light going in a straight line usually.
Now, we know light travels slower in glass, so let's add a piece of glass for each path the light takes, slowing that path just enough so its arrow ends up pointing in the same direction as all the other arrows. In other words, we want all the paths to take as much time as the longest paths.
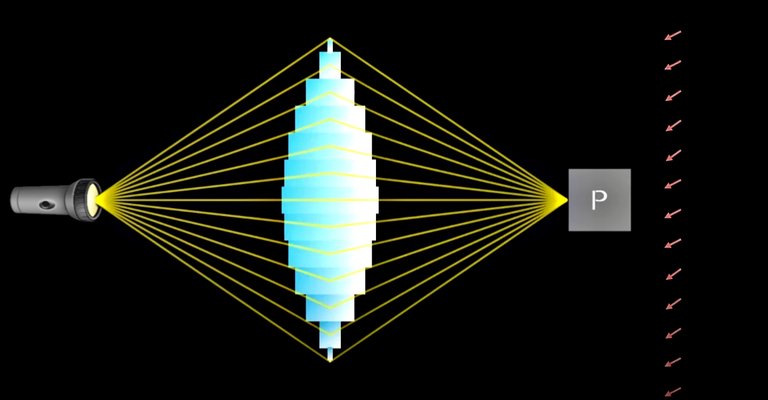
We do this to as many paths as we like, placing thinner glass as we go further to the sides, and once all their arrows point in the same direction, we now have a much longer final arrow and thus much higher probability for it arriving at our photomultiplier.
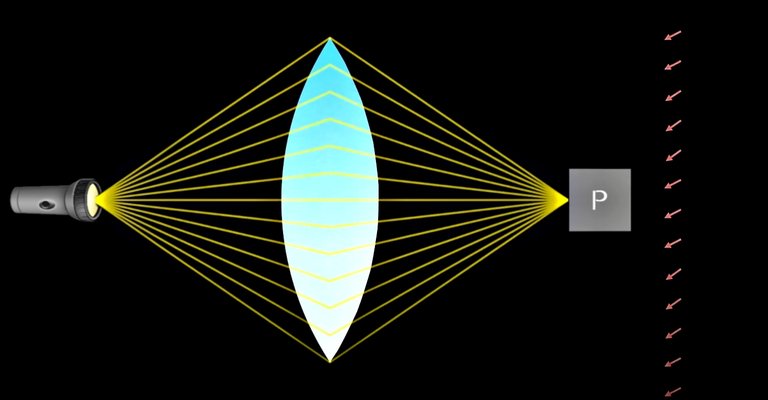
Yup! This is how a lens works, it increases the probability amplitude and hence focuses light strongly.

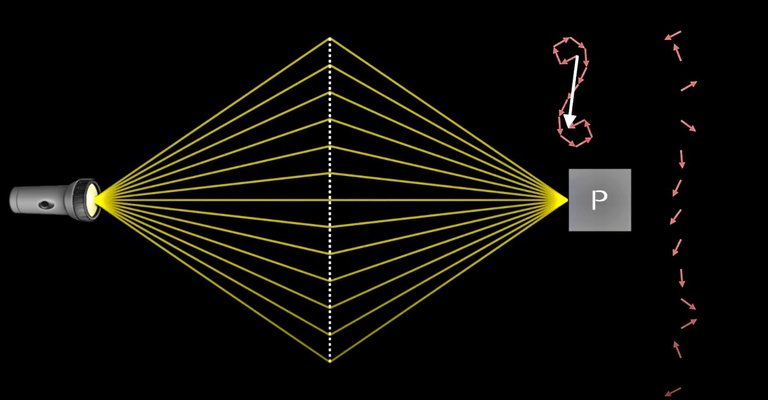
Last but not least, if we squeeze light through a hole or a slit we would be messing with its probability of detection.
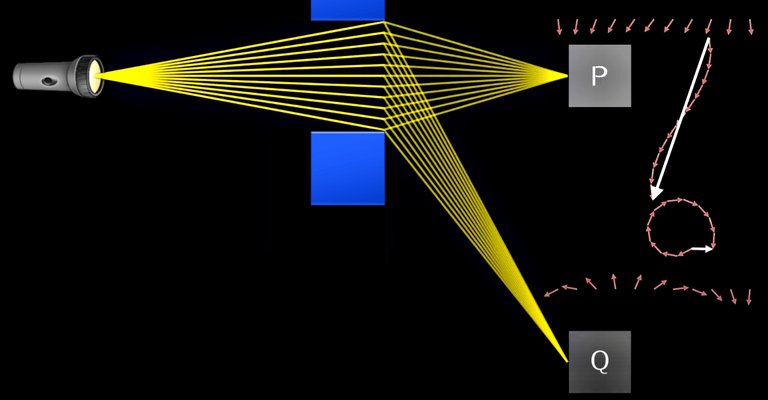
In this first example, light would end up at photomultiplier P with almost no probability ending up at photomultiplier Q.
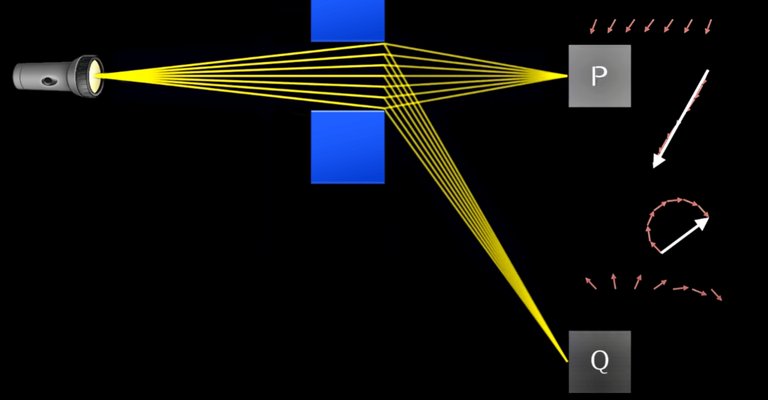
Start squeezing it, however, the arrows at the edges disappear, so the arrows at P shortens, and the arrows at Q start canceling each other less, ending up with a sizable final arrow at Q and thus higher probability for light reaching Q photomultiplier.

Squeeze it more to the limit, now there's only one path the photon can take, and add more detectors, now each of them has the same probability of a photon reaching one of them. Meaning, we are now not sure where we can detect that photon anymore. Each photomultiplier has the same probability to click.
We know that the photon went through the slit, the uncertainty about its position is really tiny. However, the photon now has an equal probability to go in any direction it wants, so now we are uncertain about its momentum.
It's worth mentioning, as noted by Lemouth in the comments that "the word uncertainty has to be taken in its statistical meaning, and not through the English definition."
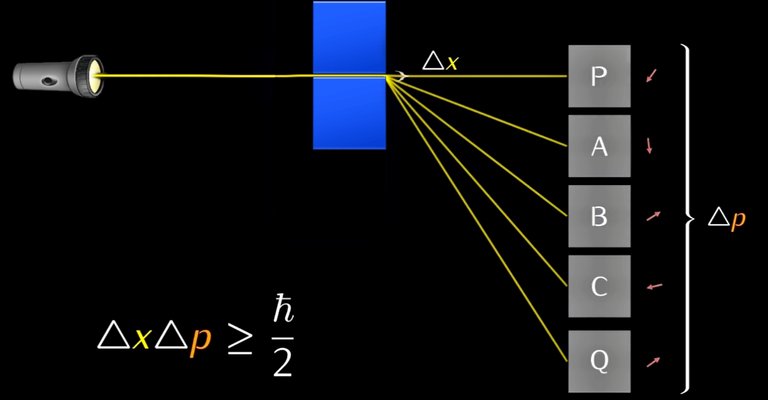
And this is the famous Heisenberg uncertainty principle!

Quantum Electrodynamics can explain almost everything in nature. In its essence, it describes how light and matter interact and it's the first theory where full agreement between quantum mechanics and special relativity has been achieved.
QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction.
It's "the jewel of physics" as Richard Feynman called it.
Until next time!

● Thank you for reading ●
● •
1- Photomultiplier tube | 2- Phasor | 3- QED: The Strange Theory of Light and Matter |





