For my English-speaking readership, this post is the adaptation in French of this one, in which I discuss all phenomena on-going in a particle collider and how to simulate them on regular computers.
J’ai pas mal parlé de mon projet de sciences citoyennes ces derniers temps, et il est temps de revenir à des posts plus classiques discutant de physique des particules et de cosmologie. Pour les sciences citoyennes, un petit peu de patience. Le coup d’envoi sera bientôt donné.
Il y a deux semaines, j’ai discuté de simulations de collisions de particules via des outils numériques automatisés. J’ai montré en particulier que ces outils permettent d’effectuer des calculs compliqués de théorie des champs quantiques sans avoir besoin de connaissances préalables sur le sujet (de sorte que c’est jouable même pour un enfant de 6 ans). Cela est possible car ces calculs peuvent être vus comme une recette qu’il suffit d’enseigner à un ordinateur. Ce dernier a au final seulement besoin de connaître le processus de collision qui nous intéresse, les détails du collisionneur et le modèle de physique des particules approprié (qui peut être le Modèle Standard ou non).
Dans le post d’aujourd’hui, je vais continuer cette discussion et expliquer comment on arrive à obtenir des simulations très proches de ce qu’il se passe dans une collision réelle. Au niveau des programmes numériques associé, il est amusant de souligner que tout est automatique, de sorte que l’utilisateur n’a pas grand chose de compliqué à faire.

[Crédits: Image originale du domaine public (CC0)]
Théorie des champs quantiques et simulations de collisions
Dans mon post précédent, nous avons discuté de collisions de protons fortement accélérés. Dans une telle configuration, le processus physique met en jeu les constituants des protons, et non pas les protons eux-mêmes. Cela provient du fait qu’à haute énergie, le proton peut être vu comme un objet dynamique fait de nombreux constituants continuellement interagissant les uns avec les autres. Il s’agit de quarks (les bloc de base les plus élémentaires de la matière), d’antiquarks (leurs antiparticules correspondant donc à de l’antimatière) et des gluons (les médiateurs de la force forte, l’une des trois interactions fondamentales du Modèle Standard). Pour plus d’informations à propos de ces particules, ne pas hésiter à jeter un œil à ce post.
Les collisions telles que celles qui ont lieu au Grand Collisionneur de Hadrons du CERN sont ainsi des collisions de quarks, d’antiquarks et de gluons. Elles permettent de produire des particules identiques ou différentes de celles de l’état initial, ces particules pouvant être connues ou hypothétiques (comme on parle de simulations, tout est permis en terme de phénomènes nouveaux).
Afin de simuler ces collisions de façon réaliste, nous allons commencer par discuter du processus dur. Ce dernier est défini par la collision de deux particules initiales (des quarks, antiquarks ou gluons) qui s’annihilent pour donner un état final particulier, comme par exemple un paire de quark-antiquark top. Pour rappel, le quark top est la particule la plus lourde du Modèle Standard et est par conséquent parfois vue comme un portail privilégié vers les phénomènes nouveaux.
La description quantitative du processus dur met en jeu un calcul de théorie des champs quantiques qui peut être fait automatiquement sur un ordinateur. Pour ce faire, on part de l’équation maîtresse de la théorie (son lagrangien) qui nous donne un ensemble de blocs de base à tout calcul. Ces blocs de base peuvent être représentés diagrammatiquement via ce que nous appelons les règles de Feynman du modèle.
Dans la partie gauche de la figure ci-dessous, on peut voir ces règles de Feynman pour le Modèle Standard.
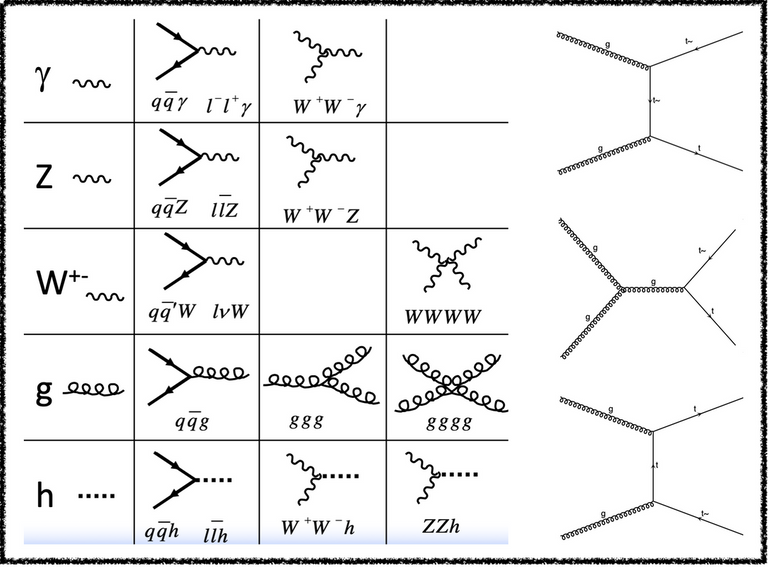
[Crédits: @lemouth]
Ces règles sont utilisées pour dessiner des diagrammes reliant l’état initial et l’état final des processus. Si de tels diagrammes ne peuvent être dessinés, alors le processus est interdit. Si au contraire, il existe certains diagrammes, alors le processus a lieu. Dans la partie droite de la figure, j’ai dessiné trois diagrammes (appelés diagrammes de Feynman) permettant de connecter un état initial contenant deux gluons à un état final mettant en jeu une paire de quark-antiquark top.
Bien que cela devient compliqué de trouver tous les diagrammes associés à un processus donné (surtout si nous avons beaucoup de particules dans l’état final), il s’agit d’une tâche suffisamment facile pour un ordinateur. Des méthodes très efficaces ont été conçues durant les dernières décennies, et nous pouvons considérer que la problématique de la recherche des diagrammes de Feynman pour un processus donné est résolue, pour tout processus et tout modèle de physique des particules.
Il nous faut ensuite convertir ces diagrammes en une équation, qui est tout simplement une intégrale fortement multiple. Cette intégrale consiste en une somme sur toutes les configurations possibles de l’état final. Par exemple, dans notre cas de paire de quark-antiquark top, on se fiche pas mal de si les particules sont produites dos-à-dos, voyagent dans la même direction ou prennent un thé. On inclut toutes ces possibilités dans l’intégrale.
Cette ‘conversion en intégrale’ fonctionne de nouveau sur base d’une recette, de sorte qu’un ordinateur peut s’en occuper tout seul comme un grand (sur base d’un algorithme qui va bien). À nouveau, nous avons un problème résolu.
Finalement, il nous faut évaluer l’intégrale numériquement. Cela se fait à l’aide d’une méthode d’intégration adaptive (comme par exemple l’algorithme VEGAS). L’avantage de cette technique est qu’elle permet d’extraire des configurations de particules et de les classer selon leur probabilité d’apparition dans la nature. C’est en fait exactement ce qu’il nous faut pour simuler des collisions telles qu’elles ont lieu dans une expérience.
Nous nous étions arrêtés ici il y a deux semaines. À présent, voyons la suite…

[Crédits: Eric Bridier (CC BY-ND 2.0)]
Particules instables et stables
Pour le moment, nous nous sommes concentrés sur la production d’un état final particulier dans une collision de particules (telles que celles qui se passent au LHC). Mais voilà, en général cet état final contient des particules lourdes et instables qui vont rapidement se désintégrer une fois produites. Par exemple, nos quarks top ci-dessus se désintègrent en un boson W et un quark bottom en environ 10-25 seconde (ce qui fait 0.0000000000000000000000001 seconde). Ensuite, ce boson W est lui-même instable et se désintègre tout aussi rapidement.
Cet ordre de grandeur nous apprend une chose : nos particules très massives peut être considérées comme se désintégrant instantanément une fois produites. La raison est que peu importe le détecteur ou l’électronique qui le compose, cela ne suffira pas pour mesurer à la fois un déplacement temporel et une différence de temps par rapport à la position et à l’instant de la collision. Pour le détecteur, tout est instantané et bien localisé dans l’espace.
Il nous faut donc ajouter les désintégrations des particules instables à l’image que nous avons construite jusqu’à présent. Il nous faut donc savoir en quoi telle ou telle particule se désintègre et avec quelle probabilité. Pour ce faire, nous allons utiliser la même technique que ci-dessus : celle des règles de Feynman. Pas besoin de réinventer la roue. Ce qui marchait avant, marche encore. Et nous pouvons ainsi le faire sur ordinateur, comme pour le processus de collision. Tout est pareil.
Cela nous amène donc naturellement à un code numérique qui inclut la production et la désintégration des particules lourdes, l’état final de la collision simulée étant constitué uniquement de particules stables. Toute particule intermédiaire instable a été traitée par l’algorithme du programme qui se charge de la simulation de sa désintégration, et nous obtenons un système fait d’électrons, de muons, de quarks légers (up, down, strange, charm et bottom), de neutrinos, de gluons et de photons. Bien sûr, il faut modifier cette liste dans le cas d’un modèle de physique différent du Modèle Standard, et y inclure toute nouvelle particule stable (comme de la matière noire).

[Crédits: CERN]
L’interaction forte se réveille
Et c’est maintenant que tout se corse…
Parmi les particules finales produites dans notre collision, nous avons des quarks et des gluons, c’est-à-dire des particules sensibles à l’interaction forte. En plus, ces particules sont vachement énergétiques. Cela a des conséquences profondes sur l’image que nous avons construites jusqu’à présent.
Les propriétés de l’interaction forte nous indiquent que toute particule fortement interagissante comme un quark ou un gluon rayonne dès qu’elle est accélérée (ce qui est notre cas ici). Une telle radiation permet de partir d’une particule très énergétique et d’aboutir à deux particules moins énergétiques. En général, ces particules se partageront l’énergie initiale de façon très asymétrique, et se déplaceront plutôt colinéairement.
Cela permet de construire une cascade de radiations. Un quark ou gluon initial très énergétique rayonne et donne lieu à deux objets un peu moins énergétiques. Ces derniers rayonnent à leur tour. Et ainsi de suite. À partir d’une seule particule, nous générons ainsi tout un tas de quarks et gluons bien collimatés. À chaque radiation, l’énergie diminue et le processus stoppe naturellement lorsque l’énergie est suffisamment petite.
Cette réaction en chaîne s’appelle une cascade partonique, et chaque quark et gluon produit dans le processus de départ en donne une. Cela est illustré sur la figure ci-dessous par tout ce qui est en rouge. Nous pouvons voir quelques particules à gauche qui rayonnent d’autres particules, qui elles-mêmes en rayonnent d’autres, jusqu’à ce que le rayonnement s’arrête aux taches vertes de la figure. À ce moment, les particules n’ont plus assez d’énergie et ne peuvent plus rayonner.
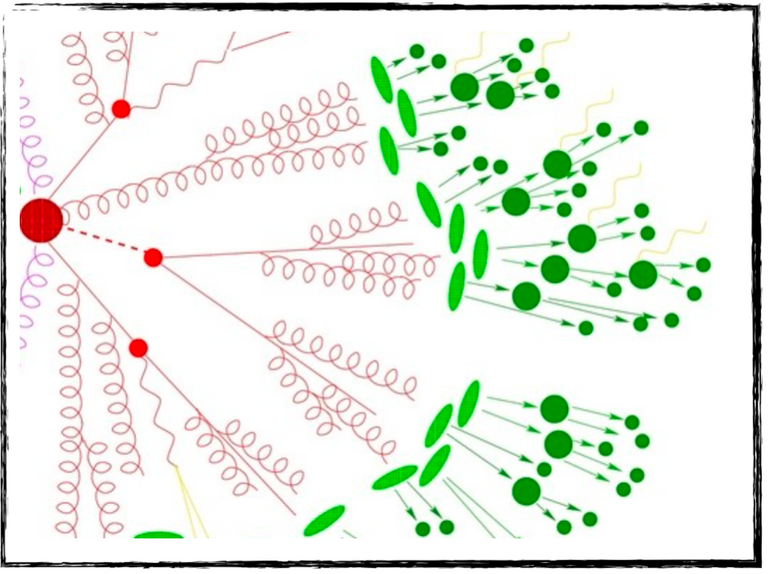
[Crédits: Un artiste de la collaboration Sherpa (image disponible partout dans la communauté de physique des hautes énergies)]
Mais que se passe-t-il au niveau de ces taches vertes ?
À cet endroit, l’interaction forte devient vraiment forte, et les quarks et gluons (qui n’existent pas en tant que particules libres dans la nature) se combinent pour former des particules composites que nous appelons hadrons (voir ici). On dit que les quarks et les gluons sont confinés dans les hadrons (sans COVID…).
Ces hadrons tout juste produits sont très instables et se désintègrent en d’autres hadrons. Cela est à nouveau illustré dans la figure ci-dessus, avec les grosses taches vertes (des hadrons plutôt lourds) qui se désintègrent en petites taches vertes (des hadrons plutôt légers). Notre collision de départ a donc mené à la production de centaines de hadrons, qui vont interagir avec un détecteur et être observés.
Les processus de cascade partonique et d’hadronisation sont tous décrits par des programmes informatiques dédiés. Les algorithmes de cascade partonique reconstruisent tout l’historique de la cascade et se basent sur un processus de chaîne de Markov. Ainsi, chaque radiation du processus est vue comme indépendante de tout le reste, et est gouvernée par une équation d’évolution venant de la théorie quantique de l’interaction forte. Cette dernière nous apprend comment un quark ou un gluon rayonne en fonction de son énergie.
Pour l’hadronisation, c’est assez différent. Il n’y a aucune équation sur laquelle nous pouvons compter, et il faut se baser sur des modèles phénoménologiques (qui ne dérivent donc pas des fondements de la théorie). Ces modèles sont cependant universels, de sorte qu’ils s’appliquent quel que soit le processus de collision.
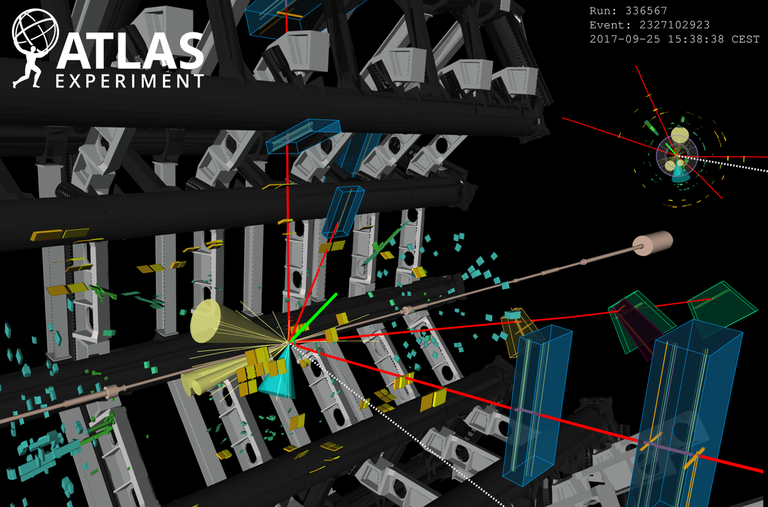
[Crédits: CERN]
Les simulations aux collisionneurs en 3 minutes
Avec ce blog, j’ai essayé de mettre en lumière comment nous pouvons simuler numériquement les collisions de particules. Cela peut se faire car tous les phénomènes impliqués sont factorisables, c’est-à-dire qu’ils peuvent se traiter indépendamment les uns des autres. Par conséquent, il existe des codes spécifiques pour chaque partie du processus complet.
Certains codes s’occupent de la production de particules connues ou nouvelles à hautes énergies, ainsi que de leur désintégration. Ils se basent sur l’automatisation de calculs de théorie des champs quantiques via les règles de Feynman. À partir de là, d’autres codes ont été conçus afin de simuler l’environnement lié à l’interaction forte, qui se trouve omniprésent dans un collisionneur tel que le Grand Collisionneur de Hadrons du CERN. Ces codes incluent la simulation des cascades partoniques (le rayonnement de particules fortement interagissantes par d’autres particules fortement interagissantes) et celle des processus d’hadronisation (formation d’objets composites faits de quarks et de gluons).
Tous les hadrons ainsi produits, ainsi que les électrons, les photons, et les muons produits directement dans la collision initiale, vont finalement interagir avec un détecteur, et y laisser des traces et des dépôts d’énergie. C’est alors notre boulot de physicien de reconstruire ce qui s’est vraiment passé lors de la collision. Après des décennies d’expérience, c’est quelque chose qu’on maîtrise plutôt pas mal, notamment grâce à nos programmes numériques.
Voilou voilà ! Je vais m’arrêter là et vous souhaite en avance un très bon week-end. A bientôt !


