
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
06-11-2024 - Analytic Geometry - Gaussian Elimination [EN]-[IT]
With this post I would like to give a brief instruction regarding the topic mentioned in the subject
(code notes: X_084)
Gaussian Elimination
The calculation of the determinant of a matrix can be done in various ways.
Today, in particular, we will see how to calculate the determinant through the Gaussian elimination method.
This method consists of transforming the original matrix into a triangular matrix. In the triangular matrix we will have the elements under the main diagonal that will be equal to zero.
When we have the matrix in triangular form, to calculate the determinant we will simply have to do the product of the elements on the main diagonal.
To be considered when applying the method
-Bring the matrix into upper triangular form, that is, transform all the elements under the main diagonal into zero.
-Each time two rows are swapped, the sign of the determinant changes, so count the number of row swaps.
-Multiply the elements of the main diagonal.
Example
Let's consider the following matrix
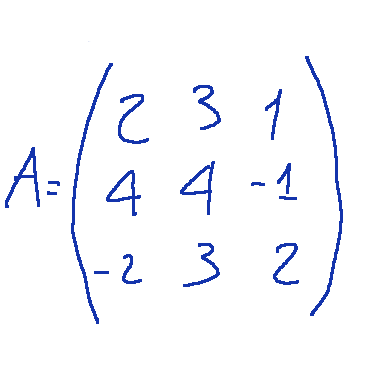
Now we have to perform the various operations to create a triangular matrix, that is, achieve the following result by managing to obtain zeros in the elements under the main diagonal.
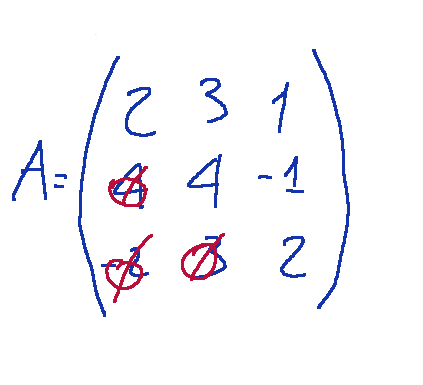
Steps to follow
Let's try to eliminate the element a21 which is now a 4 and try to transform it into a 0.
To do this, we can add the first row multiplied to the second row per−2
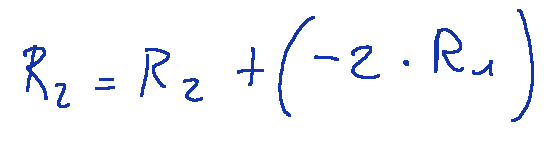
The second line would transform as follows
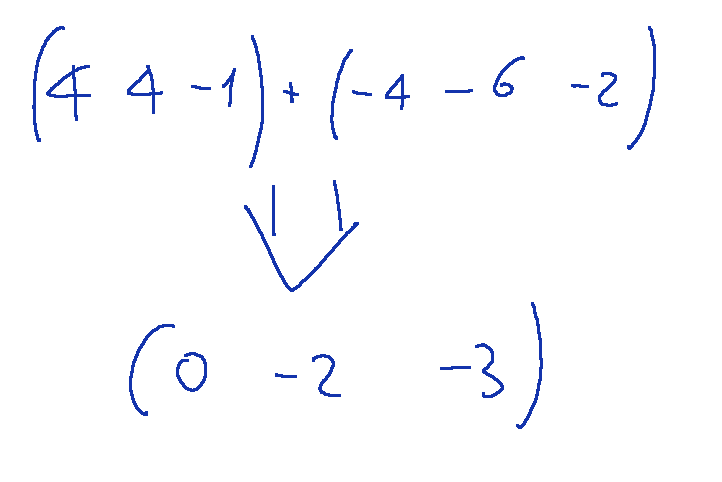
our matrix would become as continues
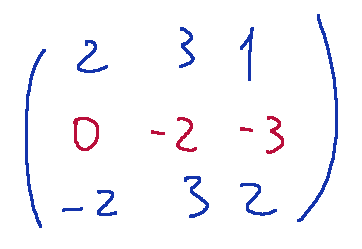
now let's proceed with the elimination of the element a31.
To do this we can transform the third row into the sum of the third row plus the product of 1 x the first row
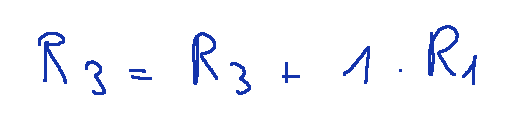
So we will have our new row 3 with the element a31 transformed to zero
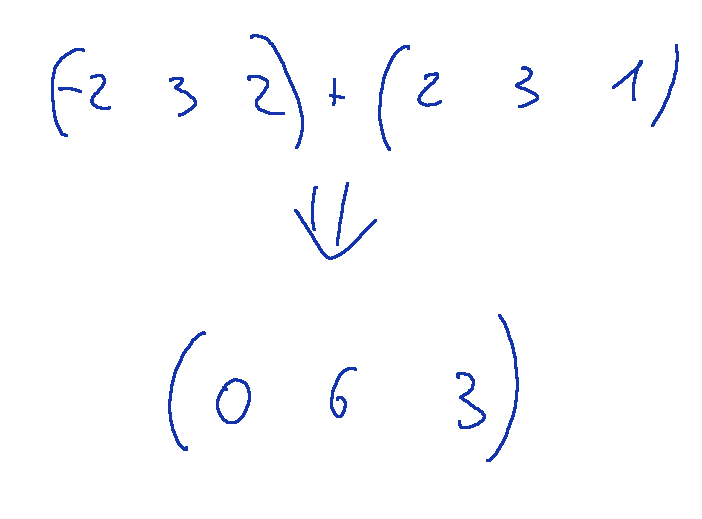
Our matrix will look like this.
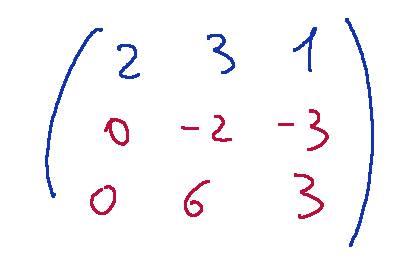
Now we need to eliminate the element a32 (third row, second column) by transforming it into zero.
First, we divide the second row by −2 to get a 1 on the diagonal
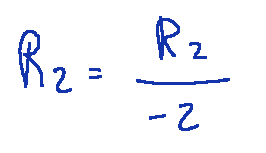
The matrix will now look like this.
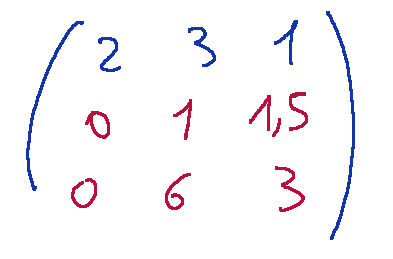
Now we need to eliminate the 6 under the pivot and we perform the following operation.
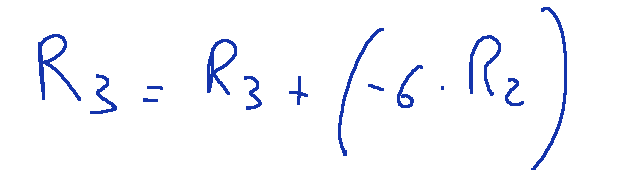
we will have the following final result
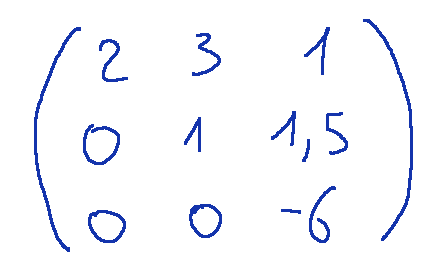
Calculating the determinant
To calculate the determinant we can now multiply the elements of the diagonal.
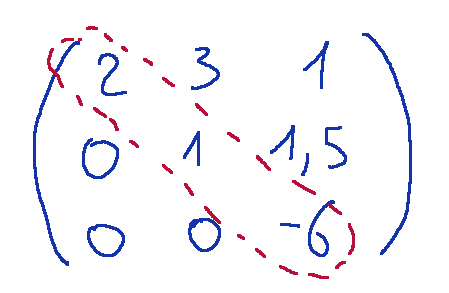
So we will have
det(A)=2⋅1⋅(−6)=−12
Conclusions
To calculate the determinant with the Gaussian elimination method, we need to transform our matrix so that we have zeros under the main diagonal and then multiply the elements that make up the main diagonal.
Question
Have you ever heard of calculating the determinant using Gaussian elimination?

[ITALIAN]
06-11-2024 - Geometria analitica - Eliminazione di Gauss [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_084)
Eliminazione di Gauss
Il calcolo del determinante di una matrice si può effettuare in vari modi.
Oggi, in particolare, vedremo come si fa calcolare il determinante tramite il modo di eliminazione di Gauss.
Questo metodo consiste nel trasformare la matrice originale in una matrice triangolare. Nella matrice triangolare avremo gli elementi sotto la diagonale principale che saranno uguali a zero.
Quando avremo la matrice in forma triangolare, per calcolare il determinante dovremo fare semplicemente il prodotto degli elementi sulla diagonale principale.
Da considerare durante l'applicazione del metodo
-Portare la matrice in forma triangolare superiore, ovvero, trasformare in zero tutti gli elementi sotto la diagonale principale.
-Ogni volta che si scambiano due righe, il segno del determinante cambia, quindi conta il numero di scambi di righe effettuati.
-Moltiplicare gli elementi della diagonale principale.
Esempio
Prendiamo in considerazione la seguente matrice
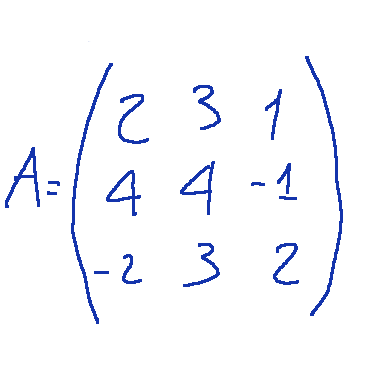
Ora dobbiamo eseguire le varie operazioni per creare una matrice triangolare, cioè raggiungere il risultato seguente riuscendo a ricavare degli zero negli elementi sotto la diagonale principale.
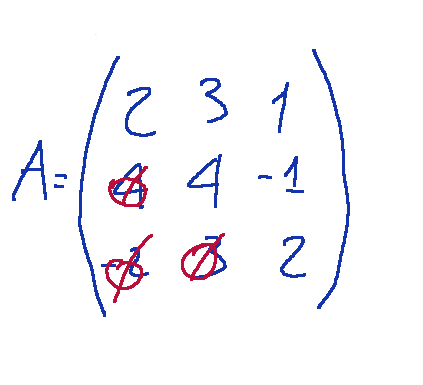
I passaggi da effettuare
Proviamo ad eliminare l'elemento a21 che ora è un 4 e cerchiamo di trasformalo appunto in uno 0.
Per farlo, possiamo sommare alla seconda riga la prima riga moltiplicata per−2
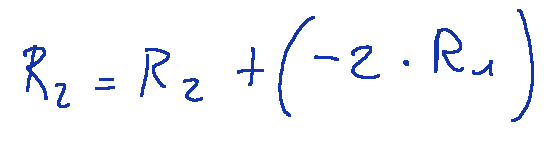
La seconda riga si trasformerebbe come segue
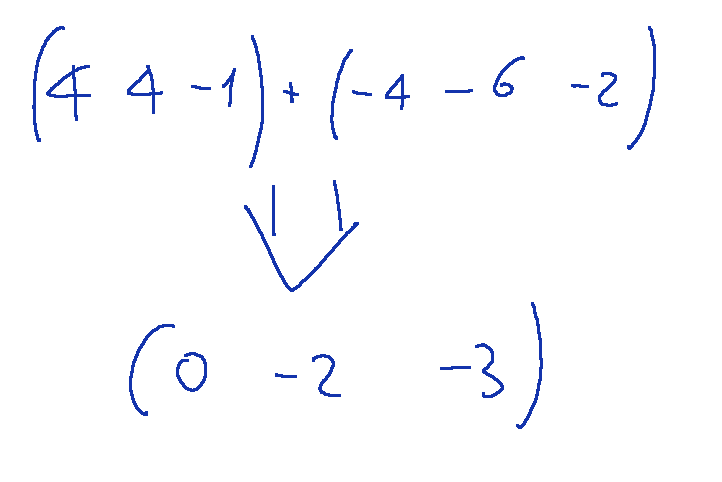
la nostra matrice diventerebbe come segue
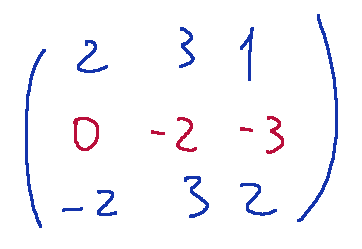
ora procediamo con l'eliminazione dell'elemento a31.
Per fare questo possiamo trasformare la terza riga nella somma tra la terza riga più il prodotto di 1 x la prima riga
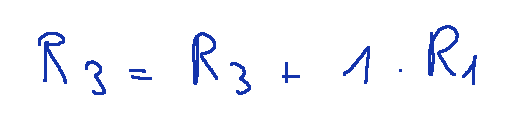
Quindi avremo la nostra nuova riga 3 con l'elemento a31 trasformato in zero
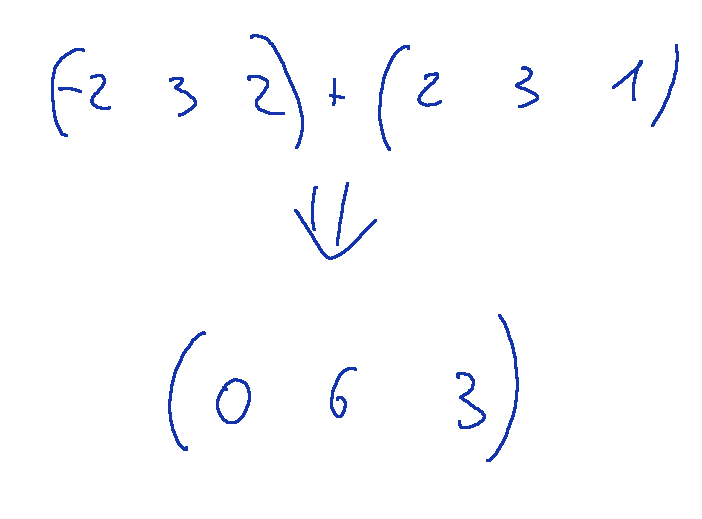
La nostra matrice si mostrerà nella seguente maniera.
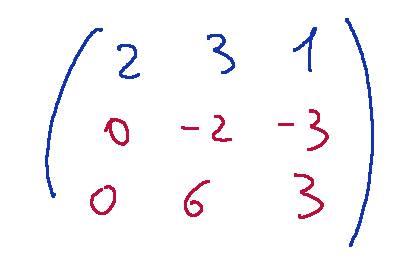
Ora dobbiamo eliminare l'elemento a32 (terza riga, seconda colonna) trasformandolo in zero.
Per prima cosa dividiamo la seconda riga per −2 in modo da ottenere un 1 nella diagonale
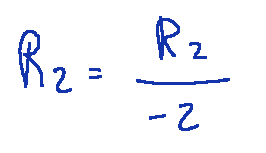
La matrice ora sarà così.
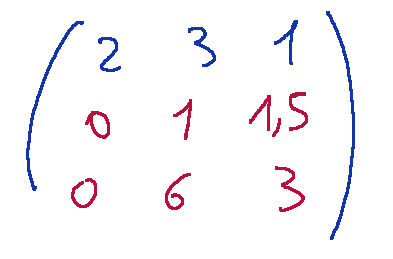
Ora dobbiamo eliminare il 6 sotto il pivot ed eseguiamo la seguente operazione.
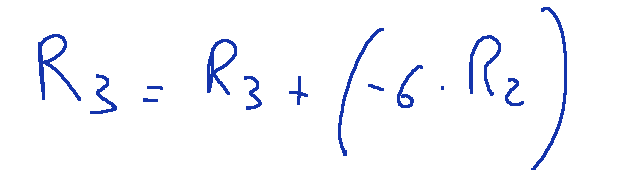
avremo il seguente risultato finale
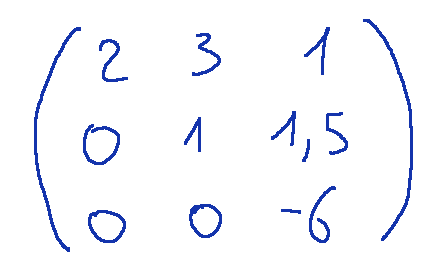
Calcolo del determinante
Per calcolare il determinante possiamo ora moltiplicare gli elementi della diagonale.
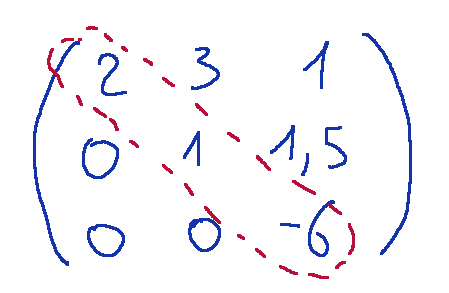
Quindi avremo
det(A)=2⋅1⋅(−6)=−12
Conclusioni
Per calcolare il determinante con il metodo dell'eliminazione di Gauss, bisogna trasformare la nostra matrice in modo da avere degli zeri sotto alla diagonale principale e poi fare la moltiplicazione degli elementi che compongono la diagonale principale.
Domanda
Avete mai sentito parlare del calcolo del determinante usando l'eliminazione di Gauss?
THE END



