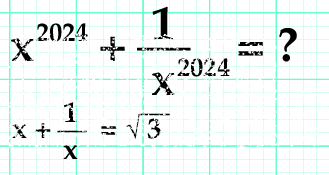Tácticas  matemáticas. Mathematical  ploys.⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

Español

Enunciado

x + 1/x = √ 3 , 1 qué vale x ²⁰²⁴ + ―― x ²⁰²⁴

Este tipo de problemas pertenecen al ámbito de las funciones simétricas y aunque es posible solucionarlos de una forma algebraica , vamos a seguir la senda del análisis combinatorio .

Preliminares

x = α , 1/x = β

-a₁= (1) = ∑ α = α + β = √ 3

a₂= (1²) = ∑ α β = α ∙ β = 1

Nos facilitan los valores de las funciones simétricas elementales (1), (1²).
Nos piden determinar el valor de la suma de potencias de índice 2024.

s₂₀₂₄ = (2024) = ∑α ²⁰²⁴= α ²⁰²⁴ + β ²⁰²⁴

Desarrollo

La relación entre las funciones simétricas elementales y la suma de potencias es la razón de ser de las identidades de Newton ,

s_n − a₁s_n-1 + a₂s_n-2 − ... + (−1)ⁿna_n = 0

Esta ecuación nos permite establecer una relación de recurrencia en s_n

s₁ = a₁
...
s_n = a₁s_n-1 − a₂s_n-2 + ... + (−1)^{n + 1}na_n

s₁= − √ 3
s₂= (− √ 3 ∙ − √ 3 ) − (2 ∙ 1) = 1

a_n= 0 , n > 2

s_n+2= − √ 3 ∙ s_n+1 − s_n

Hemos obtenido una recurrencia de orden dos, su ecuación característica determina el término general de la sucesión,

p² + √ 3 p + 1 = 0

Con soluciones,

p = e^{± i ∙5/6∙π}

De la naturaleza de las soluciones de la ecuación característica inferimos que la sucesión es periódica,

5/6 ∙ n = 2k
5n = 12k
n = 12

∴ s_n+12= s_n
s_n+6 = -s_n

Resolución

Solución

2024 ≡ 8 mod 12

s₂₀₂₄ = s₈= - s₂

s₂₀₂₄ = - 1

∎

English

Español

Statement

x + 1/x = √ 3 , 1 calculate x ²⁰²⁴ + ―― x ²⁰²⁴

This is a problem on symmetric functions , solvable by pure algebraic methods, but here we are taking the combinatorial route and seeing...

Prelude

x = α , 1/x = β

-a₁= (1) = ∑ α = α + β = √ 3

a₂= (1²) = ∑ α β = α ∙ β = 1

We know value of the elementary symmetric functions (1), (1²).
We are asked for the value of the powers sum with 2024 index .

s₂₀₂₄ = (2024) = ∑α ²⁰²⁴= α ²⁰²⁴ + β ²⁰²⁴

Development

Symmetric elementary functions related to powers sum ones by means of the Newtonian identities ,

s_n − a₁s_n-1 + a₂s_n-2 − ... + (−1)ⁿna_n = 0

That is a recurrence relation on s_n,

s₁ = a₁
...
s_n = a₁s_n-1 − a₂s_n-2 + ... + (−1)^{n + 1}na_n

s₁= − √ 3
s₂= (− √ 3 ∙ − √ 3 ) − (2 ∙ 1) = 1

a_n= 0 , n > 2

s_n+2= − √ 3 ∙ s_n+1 − s_n

We have a recurrence of second order, the general term is formed with solutions of its characteristic equation ,

p² + √ 3 p + 1 = 0

p = e^{± i ∙5/6∙π}

We can infer that the sequence is periodic as the solutions of its charaterisitic equation .

5/6 ∙ n = 2k
5n = 12k
n = 12

∴ s_n+12= s_n
s_n+6 = -s_n

Solution

Answer

2024 ≡ 8 mod 12

s₂₀₂₄ = s₈= - s₂

s₂₀₂₄ = - 1

∎

Media

Sort:

Trending

[-]

hivebuzz 6 months ago

Congratulations @j2e2xae! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)

You distributed more than 300 upvotes.
Your next target is to reach 400 upvotes.

_{You can view your badges on your board and compare yourself to others in the Ranking}
_{If you no longer want to receive notifications, reply to this comment with the word STOP}

0.00 VYB

Tácticas matemáticas. Mathematical ploys.⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

Enunciado

x + 1/x = √ 3 , 1qué vale x 2024 + ―― x 2024

Preliminares

x = α , 1/x = β-a1 = (1) = ∑ α = α + β = √ 3 a2 = (12 ) = ∑ α β = α ∙ β = 1

s2024 = (2024) = ∑α 2024 = α 2024 + β 2024

Desarrollo

sn − a1sn-1 + a2sn-2 − ... + (−1)nnan = 0

s1 = a1 ... sn = a1sn-1 − a2sn-2 + ... + (−1)n + 1nan

s1 = − √ 3 s2 = (− √ 3 ∙ − √ 3 ) − (2 ∙ 1) = 1 an = 0 , n > 2 sn+2 = − √ 3 ∙ sn+1 − sn

p2 + √ 3 p + 1 = 0

p = e ± i ∙5/6∙π

5/6 ∙ n = 2k 5n = 12k n = 12 ∴ sn+12 = sn sn+6 = -sn

Resolución

Solución

2024 ≡ 8 mod 12s2024 = s8 = - s2s2024 = - 1

Statement

x + 1/x = √ 3 , 1calculate x 2024 + ―― x 2024

Prelude

x = α , 1/x = β-a1 = (1) = ∑ α = α + β = √ 3 a2 = (12 ) = ∑ α β = α ∙ β = 1

s2024 = (2024) = ∑α 2024 = α 2024 + β 2024

Development

sn − a1sn-1 + a2sn-2 − ... + (−1)nnan = 0

s1 = a1 ... sn = a1sn-1 − a2sn-2 + ... + (−1)n + 1nan

s1 = − √ 3 s2 = (− √ 3 ∙ − √ 3 ) − (2 ∙ 1) = 1 an = 0 , n > 2 sn+2 = − √ 3 ∙ sn+1 − sn

p2 + √ 3 p + 1 = 0

p = e ± i ∙5/6∙π

5/6 ∙ n = 2k 5n = 12k n = 12 ∴ sn+12 = sn sn+6 = -sn

Solution

Answer

2024 ≡ 8 mod 12s2024 = s8 = - s2s2024 = - 1

Tácticas  matemáticas. Mathematical  ploys.⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀

x + 1/x = √ 3 ,

1
qué vale x ²⁰²⁴ + ――
x ²⁰²⁴

x = α , 1/x = β

-a₁= (1) = ∑ α = α + β = √ 3

a₂= (1²) = ∑ α β = α ∙ β = 1

s₂₀₂₄ = (2024) = ∑α ²⁰²⁴= α ²⁰²⁴ + β ²⁰²⁴

s_n − a₁s_n-1 + a₂s_n-2 − ... + (−1)ⁿna_n = 0

s₁ = a₁
...
s_n = a₁s_n-1 − a₂s_n-2 + ... + (−1)^{n + 1}na_n

s₁= − √ 3
s₂= (− √ 3 ∙ − √ 3 ) − (2 ∙ 1) = 1

a_n= 0 , n > 2

s_n+2= − √ 3 ∙ s_n+1 − s_n

p² + √ 3 p + 1 = 0

p = e^{± i ∙5/6∙π}

5/6 ∙ n = 2k
5n = 12k
n = 12

∴ s_n+12= s_n
s_n+6 = -s_n

2024 ≡ 8 mod 12

s₂₀₂₄ = s₈= - s₂

s₂₀₂₄ = - 1

x + 1/x = √ 3 ,

1
calculate x ²⁰²⁴ + ――
x ²⁰²⁴

x = α , 1/x = β

-a₁= (1) = ∑ α = α + β = √ 3

a₂= (1²) = ∑ α β = α ∙ β = 1

s₂₀₂₄ = (2024) = ∑α ²⁰²⁴= α ²⁰²⁴ + β ²⁰²⁴

s_n − a₁s_n-1 + a₂s_n-2 − ... + (−1)ⁿna_n = 0

s₁ = a₁
...
s_n = a₁s_n-1 − a₂s_n-2 + ... + (−1)^{n + 1}na_n

s₁= − √ 3
s₂= (− √ 3 ∙ − √ 3 ) − (2 ∙ 1) = 1

a_n= 0 , n > 2

s_n+2= − √ 3 ∙ s_n+1 − s_n

p² + √ 3 p + 1 = 0

p = e^{± i ∙5/6∙π}

5/6 ∙ n = 2k
5n = 12k
n = 12

∴ s_n+12= s_n
s_n+6 = -s_n

2024 ≡ 8 mod 12

s₂₀₂₄ = s₈= - s₂

s₂₀₂₄ = - 1