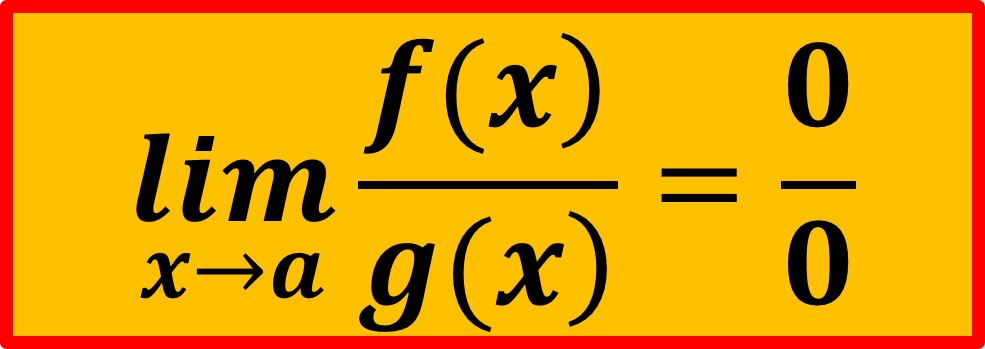
Let's start with the following one:
Find the following limit:
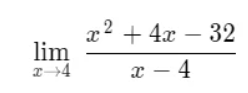
On evaluating the limit, we find that it is of the form 0/0, i.e., it is an indeterminate limit.
This is:
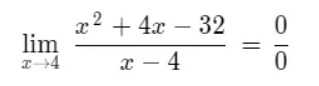
To eliminate the indeterminacy we are going to apply Ruffini's Rule to factor a polynomial.
First, we must make sure that the polynomial that we are going to factor, applying this rule, is ordered preferably in decreasing order.
Let's get started:
In this case, the polynomial to be factored is in the numerator, is of degree 2, is complete and is in decreasing order.
So, let's get started:
In the image below, you will notice that first I have identified the coefficients of the polynomial, they are: 1,4 and 32; then, below the coefficients, I have drawn a galley, in the upper left area of the galley we place the value to which the x tends, in this case it is 4. Then we lower the coefficient 1 below the galley and multiply it by 4, the result of this we place it below the coefficient 4, and as both have the same sign, we add them and it gives us 8; this 8 we multiply it by 4 and it gives us 32 positive, which we place below -32, and we add, as both have different signs, this gives us 0, which is the desired result.
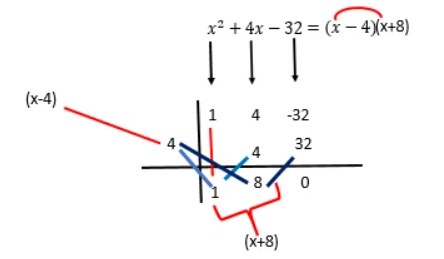
From here we get two factors, the first one is (x-4) which is obtained by subtracting to the variable x the value to which the x tends; and the second factor is (x+8), which results from the identification of the values that are under the galley, they are: 1 and 8, then the factor is 1x+8=x+8.
Finally:
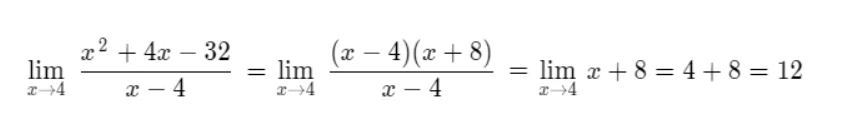
This leads to the desired result.
Here is another example:
Find the following limit:
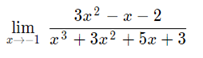
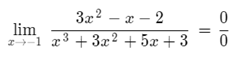
When evaluated we get indeterminate
Let's apply Ruffini
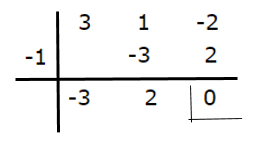
The factorization of the numerator is as follows:
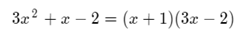
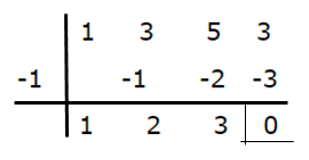
Let's continue with the denominator
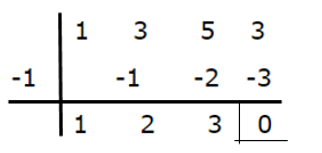
The factorization of the denominator is as follows:
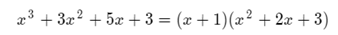
In short, this is the development of the exercise and its solution:


The text and images are completely original.

