Introduction
Hartree-Fock theory is used to describe chemical systems and predict properties such as bond angle, bond length. For this purpose, various approximations are made to the exact quantum mechanical description of the system and then the Schrödinger equation is solved.
So, the first thing we need to clarify is what the Schrödinger equation is all about. The Schrödinger equation represents a partial differential equation, which acts on a wave function. It represents a postulate of the quantum mechanics that all particles can be described with a wave function. The Schrödinger equation has the following form:
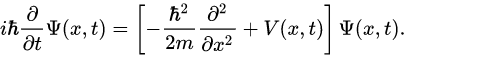
The first part in the brackets stands for the kinetic energy, represented by the momentum operator, while the second part describes the potential energy.
Now what about the chemistry part?!
As you probably know, electrons and protons are not the smallest possible particles. There are numerous other particles in the so-called particle zoo. In chemistry, however, the properties of bonds are mainly described by the behavior of the electrons or atomic nuclei. So the first assumption we make is that we define the atomic nuclei and electrons as our elementary particles.
We describe the interactions between the different particles by means of the classical Couloumb forces. We define the Hamilton operator as follows:
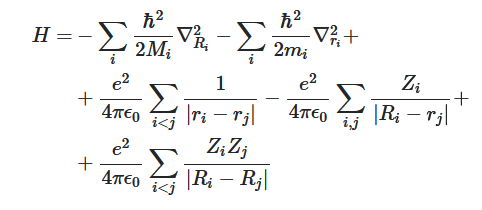
Hamilton operator describing a system of nuclei and electrons.
Already here it becomes clear that without further assumptions we will have a hard time to solve this equation for arbitrary systems. After all it is a well known fact that there is no closed solution for the N-body problem with N > 2.
So we introduce the next approximation. The Born-Oppenheimer approximation. Since the nuclei are much heavier than the electrons, we assume that the nuclei are stationary from the point of view of the electrons. The equation can then be separated into a product of two independent equations. One describes the behavior of the nucleus and one the behavior of the electrons.
Now the question arises how to solve the equation describing the electrons. After all, this is still a many-particle problem. This many-particle problem cannot actually be separated because of the Coulomb forces. Nevertheless, we assume that we can write the wave function for each electron individually and use a product of all wave functions as the total wave function. However, the wave function must satisfy the antisymmetry principle. This means that the wave function must change sign when two electrons are exchanged. This is not the case with a simple product. Therefore, we use the Slater determinant as the product.
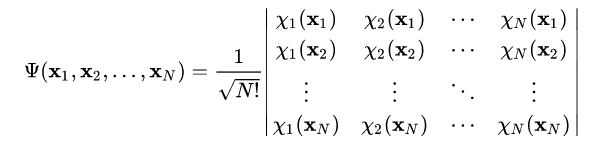
The slater determinant which approximates our many electron wave function.
As a basis for the Slater determinant we now choose one particle functions, so-called orbitals.
Minimize the energy!
Now the task is to choose the one-particle functions optimally. The variation principle helps us to do this. It states that the minimum possible energy corresponds to the ground state energy. So we can try to minimize the energy and the smaller the energy becomes, the closer we are to the exact energy. We use a well-known tool from mathematics called Lagrange multipliers to find the orbitals that minimize the energy. This leads us to the Hartree-Fock equations:
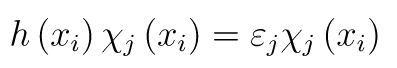
The Hartree-Fock equations.
Introduce a basis
But even these equations are still difficult to solve. For this we now use the following trick. We introduce a set of known functions and represent the unknown functions as a linear combination of the known functions. Therefore we only have to find the coefficients of the linear combination which minimize the energy. This results in the Roothaan-Hall equations:
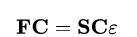
The Roothaan-Hall matrix equation.
These equations can be solved using an initial guess and the self-consistent field method. This is an iterative method.
Conclusions
There are quite a few approximations and assumptions that go into the Hartree-Fock theory. Nevertheless, it describes certain systems with good accuracy and it can be further improved e.g. with perturbation calculations.
Sources
[1] Szabo A. & Ostlund N. S. (1996). Modern quantum chemistry : introduction to advanced electronic structure theory. Dover Publications.
[2] Cramer C. J. (2008). Essentials of computational chemistry : theories and models (2nd ed. repr). Wiley.
