▶️ Watch on 3Speak - Odysee - BitChute - Rumble - YouTube - PDF notes

---

In this video I go over the end-of-chapter Problems Plus advanced math problems for the Vectors and Geometry of Space chapter. There are 8 problems in total and cover 3D geometry, surfaces, vectors, vector projections, and applications to physics and airplane dynamics. It's 4 hours of advanced math so buckle up!

Timestamps

• Intro: 0:00
• Calculus Book Reference: 0:56
• Sections in Calculus Book Chapter: 1:10
• Topics to Cover: 2:02
• Review: Concept Check: 19 Questions: 2:19

1. Problem 1: Tightly packed balls in a box: 2:22
   • Hint: Use analogy problem solving strategy: 3:32
   • Solution: Solving the 2D case first: 4:51
   • Solving the 3D case: 9:32
2. Problem 2: Volume around a box: 18:25
   • Solution: Solving the 2D case first: 19:07
   • Solving the 3D case: 22:19
3. Problem 3: Intersecting planes: 33:57
   • Solution to (a): Symmetric equations for the line: 34:56
   • Solution to (b): Curve of intersection as c varies: 1:02:13
   • Solution to (c): Volume of hyperboloid surface: 1:23:25
4. Problem 4: Playing flying in wind: 1:27:32
   • Solution to (a): Wind velocity: 1:28:30
   • Solution to (b): Modified plane velocity: 1:39:21
5. Problem 5: Sum of vector projections: 1:50:46
   • Recap on the Geometric series: 2:10:31
6. Problem 6: Largest sphere in a sphere: 2:13:27
7. Problem 7: Block on an inclined plane: 2:41:46
   • Solution to (a): Coefficient of static friction: 2:46:29
   • Solution to (b): Applying a minimal horizontal force: 2:51:16
   • Solution to (c): Minimal horizontal force formula: 3:05:16
   • Solution to (d): Maximum horizontal force: 3:15:47
8. Problem 8: Volume of a solid from its shadows: 3:35:32
   • Solution to (a): Volume of largest such solid: 3:37:24
   • Solution to (b): No smallest volume: 4:08:26

• Outro: 4:11:21

---

Video sections playlist - Vectors and the Geometry of Space playlist

---

View Video Notes Below!

---

Become a MES Super Fan - Donate - Subscribe via email - MES merchandise

• MES Links webpage - MES Links Telegram - MES Truth

Reuse of my videos:

• Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

• Bookmark sites/channels/accounts and check periodically.
• Remember to always archive website pages in case they get deleted/changed.

Recommended Books: "Where Did the Towers Go?" by Dr. Judy Wood

Join my forums: Hive community - Reddit - Discord

Follow along my epic video series: MES Science - MES Experiments - Anti-Gravity (MES Duality) - Free Energy - PG

---

NOTE 1: If you don't have time to watch this whole video:

• Skip to the end for Summary and Conclusions (if available)
• Play this video at a faster speed.
  -- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
  -- MES tutorial
• Download and read video notes.
• Read notes on the Hive blockchain $HIVE
• Watch the video in parts.
  -- Timestamps of all parts are in the description.

Browser extension recommendations: Increase video speed - Increase video audio - Text to speech (Android app) – Archive webpages

---

Vectors and the Geometry of Space: Review

Concept Check: Review

---

Sections in Calculus Book Chapter

I have made a list of the sections in this particular chapter with links to the Hive post of the videos I have already finished.

Note that I have started splitting each long video into sections and made a playlist for each.

Vectors and the Geometry of Space

1. 3-D Coordinate Systems
2. Vectors
   • Complex Numbers as Rotation Matrices (Playlist)
3. The Dot Product - Playlist
4. The Cross Product - Playlist
   • Discovery Project: The Geometry of a Tetrahedron - Playlist
5. Equations of Lines and Planes - Playlist
   • Laboratory Project: Putting 3D in Perspective - Playlist
6. Cylinders and Quadric Surfaces - playlist
7. Review - playlist
   • True-False Quiz
8. Problems Plus - ▶️

---

Topics to Cover

Note that the timestamps will be included in the video description for each topic listed below.

1. Problem 1: Tightly packed balls in a box
2. Problem 2: Volume around a solid box
3. Problem 3: Intersecting Planes
4. Problem 4: Plane flying in wind
5. Problem 5: Sum of vector projections
6. Problem 6: Largest sphere in a sphere
7. Problem 7: Block on an inclined plane
8. Problem 8: Volume of a solid from its shadows

---

Problems Plus

---

Problem 1: Tightly packed balls in a box

Each edge of a cubical box has length 1 m.

The box contains nine spherical balls with the same radius r.

The center of one ball is at the center of the cube and it touches the other eight balls.

Each of the other eight balls touches three sides of the box.

Thus the balls are tightly packed in the box, as in the figure below.

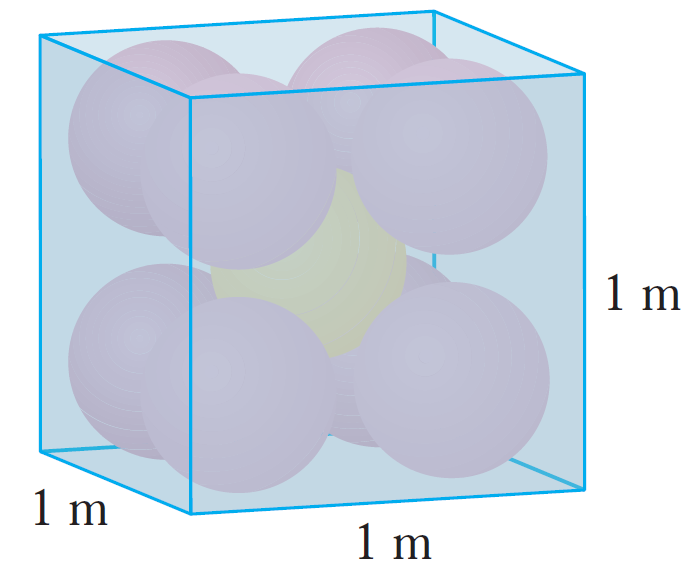
Find r.

Hint: If you have trouble with this problem, read about the problem-solving strategy:

Use Analogy

Try to think of an analogous problem, that is, a similar problem, a related problem, but one that is easier than the original problem.

If you can solve the similar, simpler problem, then it might give you the clues you need to solve the original, more difficult problem.

For instance, if a problem involves very large numbers, you could first try a similar problem with smaller numbers.

Or if the problem involves three-dimensional geometry, you could look for a similar problem in two-dimensional geometry.

Or if the problem starts with is a general one, you could first try a special case.

Solution: Solving the 2D Case First

Since three-dimensional situations are often difficult to visualize and work with, let us first try to find an analogous problem in two dimensions.

The analogue of a cube is a square and the analogue of a sphere is a circle.

Thus a similar problem in two dimensions is the following:

If five circles with the same radius r are contained in a square of side 1 m so that the circles touch each other and four of the circles touch two sides of the square, find r.

The diagonal of the square can be determined by the Pythagorean theorem:

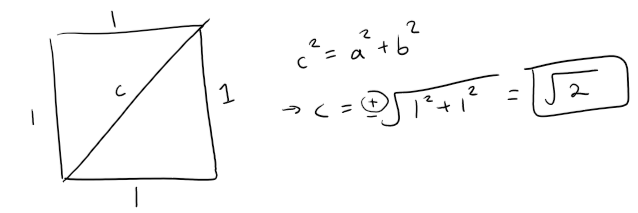
Let's write the diagonal of the square as a function of r and x, where x is the diagonal of a smaller square of side r, and solve for r.

Solving the 3D Case

Let's use these ideas to solve the original three-dimensional problem.

The diagonal of the cube can be determined using the distance formula in 3D:

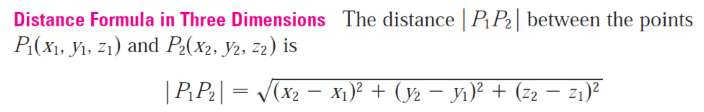
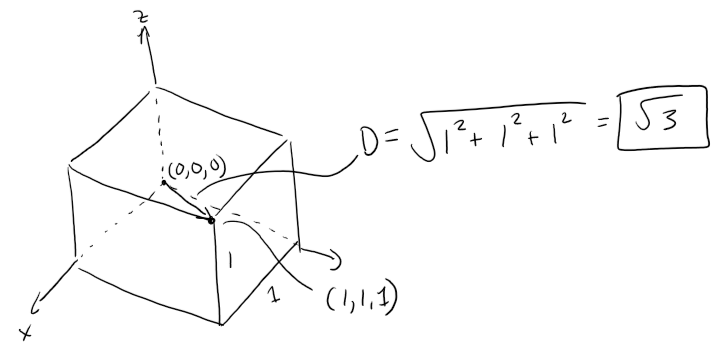
Let's write the diagonal of the cube as a function of r and x, where x is the diagonal of a smaller cube with edge r, and solve for r.

---

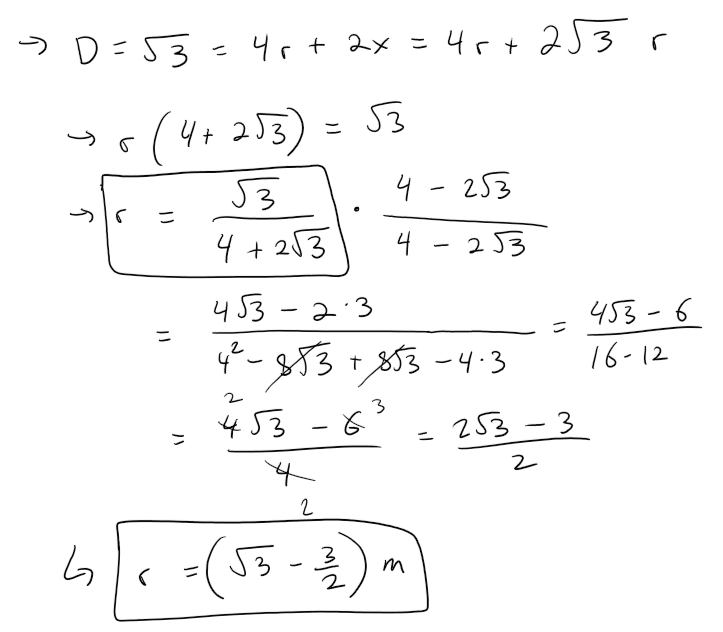
Problem 2: Volume around a solid box

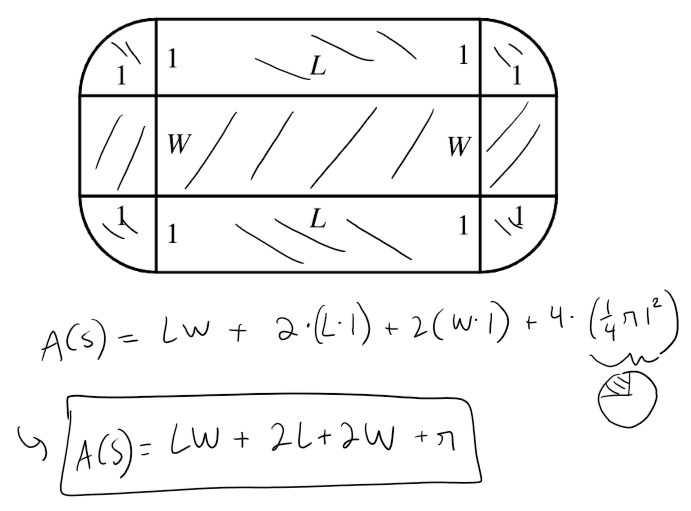
Let B be a solid box with length L, width W, and height H.

Let S be the set of all points that are a distance at most 1 from some point on B.

Express the volume of S in terms of L, W, and H.

Solution: Solve the 2D Case First

Let's try an analogous problem in two dimensions first.

Consider a rectangle with length L and width W and find the area of S in terms of L and W.

Solving the 3D Case

Now in three dimensions, the volume of S is:

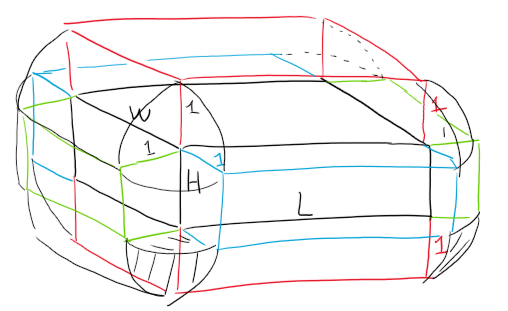
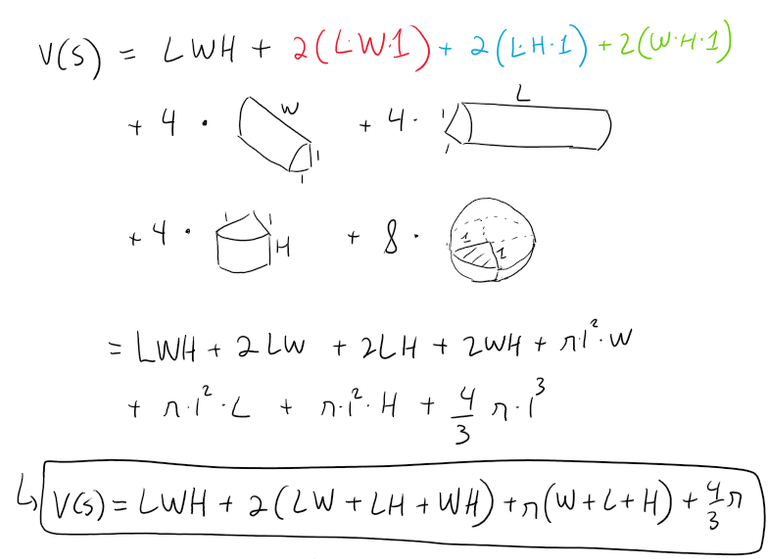
Note the equation of a sphere is 4/3∙πr³.

---

Problem 3: Intersecting Planes

Let L be the line of intersection of the planes:

cx + y + z = c

x - cy + cz = -1

where c is a real number.

(a) Find the symmetric equations for L.

(b) As the number c varies, the line L sweeps out a surface S.

Find an equation for the curve of intersection of S with the horizontal plane z = t (the trace of S in the plane z = t).

(c) Find the volume of the solid bounded by S and the planes z = 0 and z = 1.

Solution to (a):

We can find the line of intersection L as in my earlier example.

Observe that the point (-1, c, c) lies on both planes.

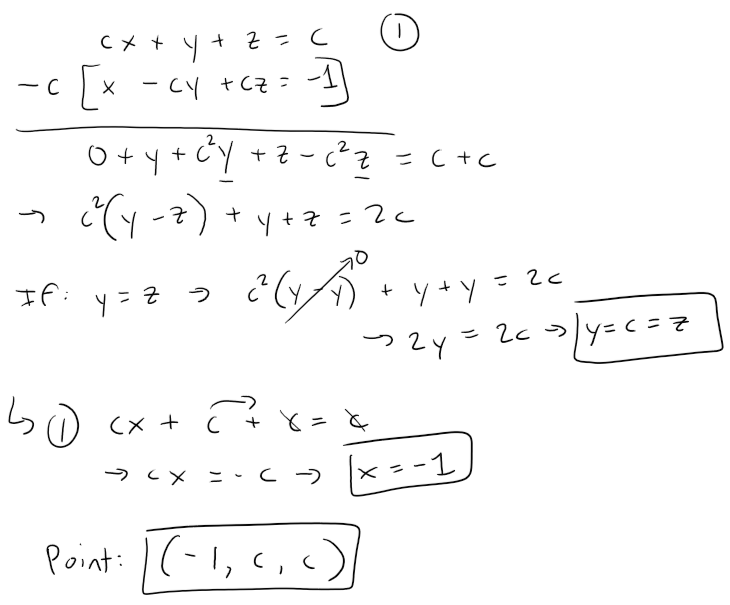
Recall also that the normal vectors of each plane is included in their linear equations, as per my earlier video.

Now since L lies in both planes, it is perpendicular to both the normal vectors n₁ and n₂, thus parallel to their cross product.

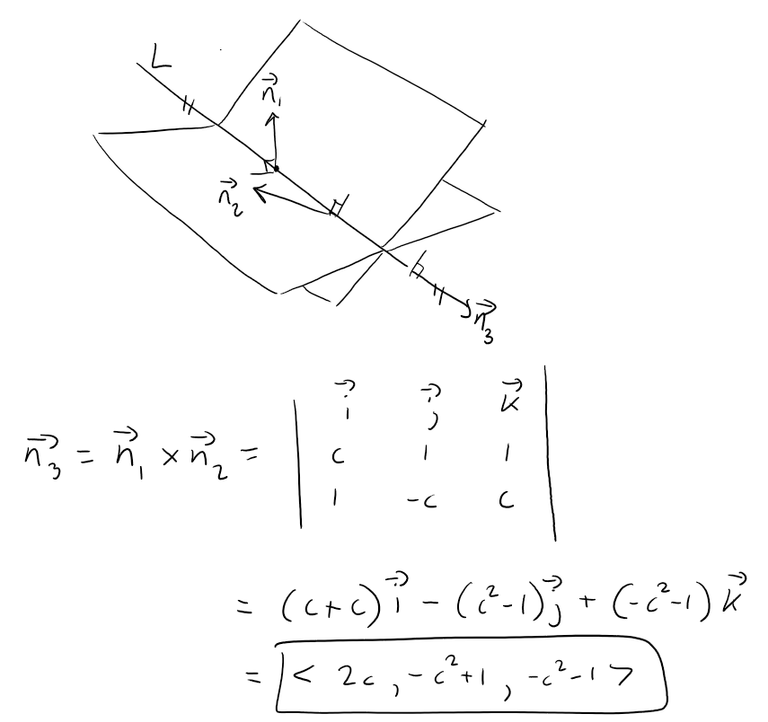
Thus we can obtain the symmetric equations of L:

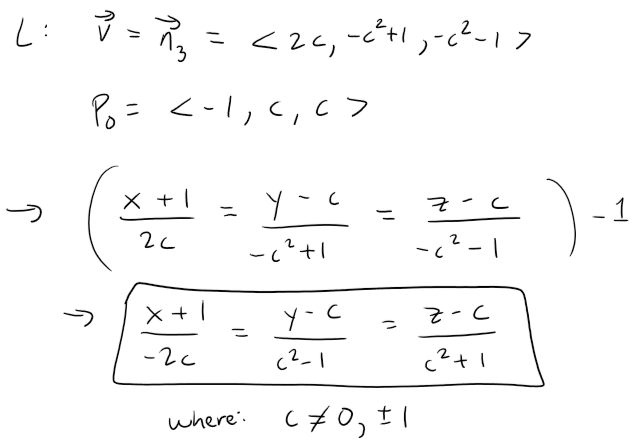
If c = 0, then the two planes are given by the equations:

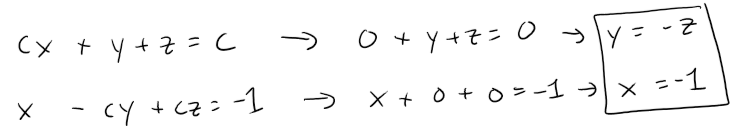
If c = -1, then the two planes are given by the equations.

Note that the solution manual made a typo in this part, and is wrong.

If c = 1, then the two planes are given by the equations:

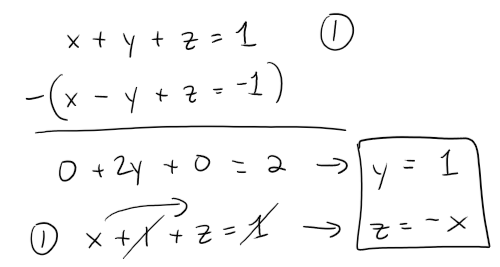
Note that the solution manual made a typo in this part as well.

We can double check our work by graphing in the GeoGebra 3D graphing calculator:
https://www.geogebra.org/calculator/qq2rx3zd

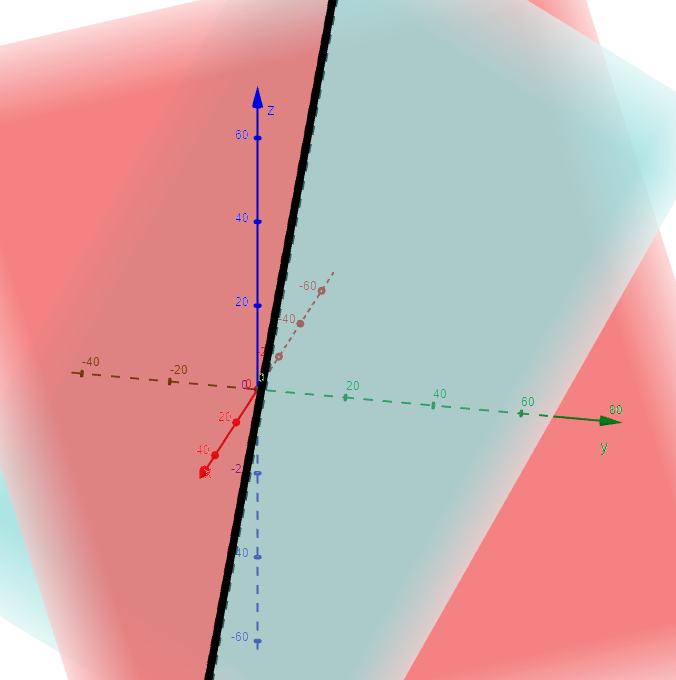
Solution to (b)

Let's visualize the question.

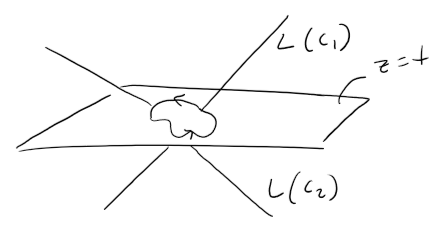
If we set z = t in the symmetric equations and solve for x and y separately we get:

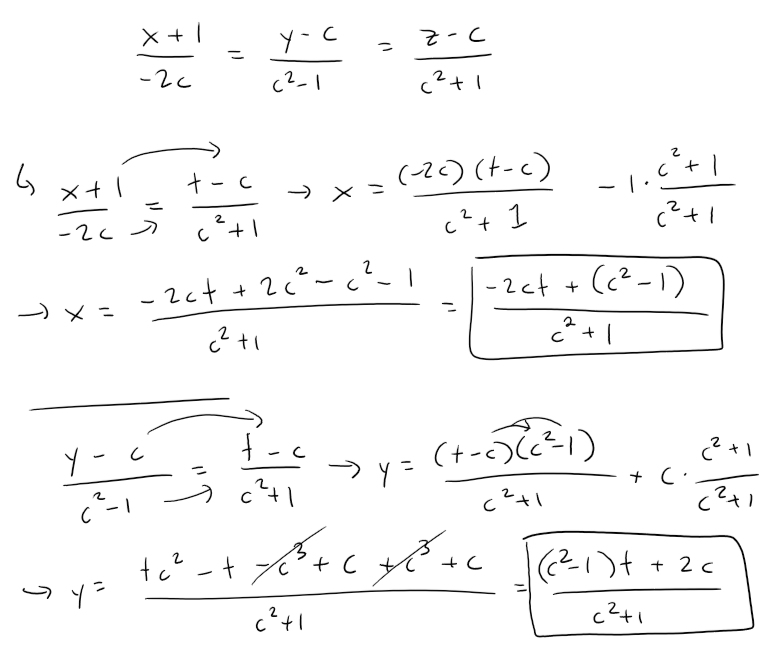
To eliminate c from these equations, we can work with the squares x² and y²:

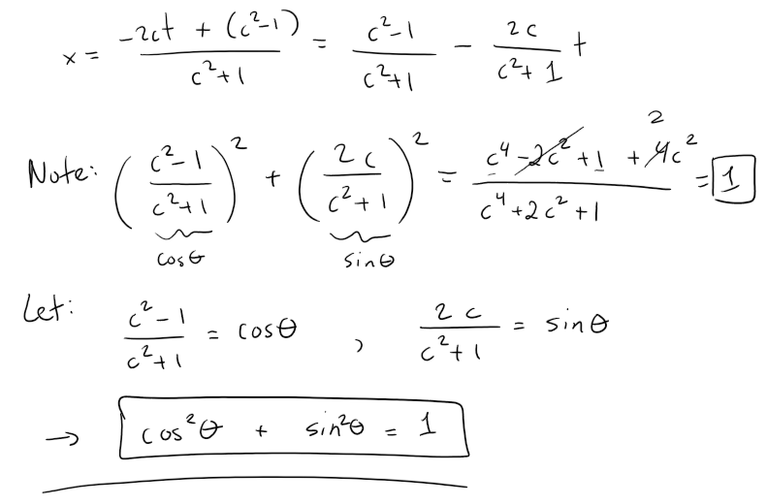
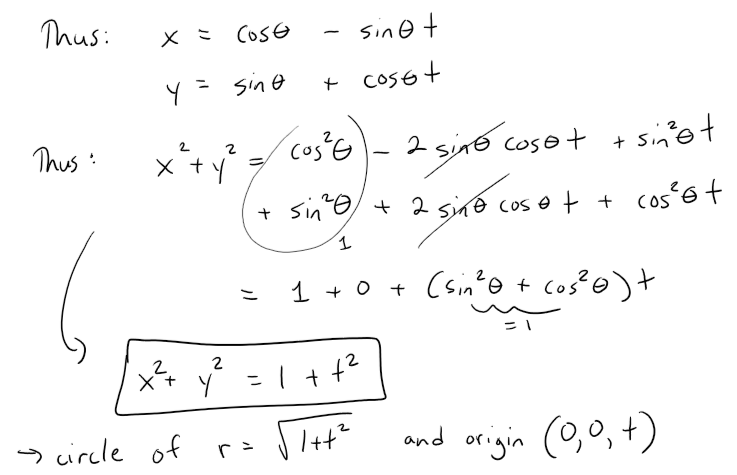
We can graph this out in GeoGebra: https://www.geogebra.org/calculator/qq2rx3zd

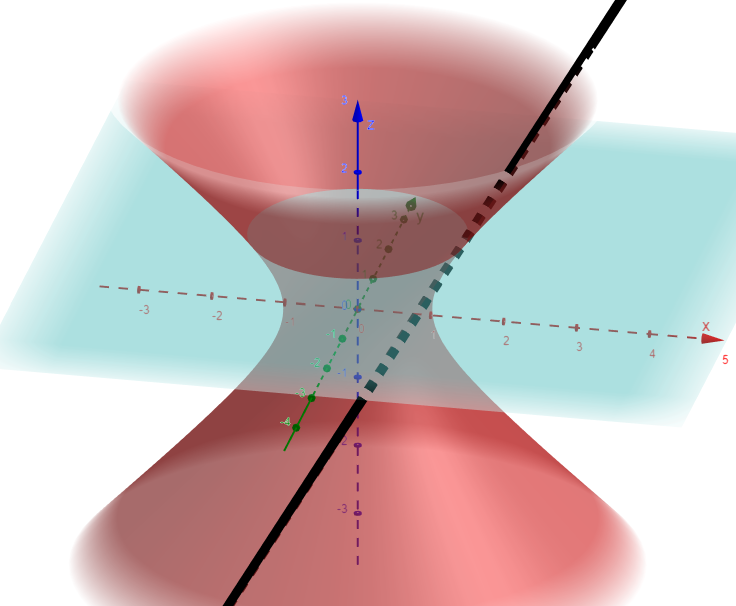
Note the surface S(x² + y² - z² = 1), is a hyperboloid of one sheet.

Solution to (c)

Since we know the cross section of the hyperboloid of one sheet surface S is a circle and its radius, we can determine the volume of S between the planes z = 0 and z = 1.

---

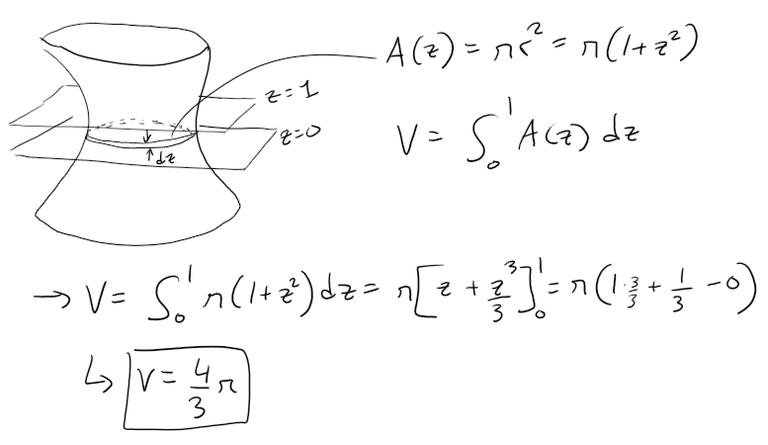
Problem 4: Plane flying in wind

A plane is capable of flying at a speed of 180 km/h in still air.

The pilot takes off from an airfield and heads due north according to the plane's compass.

After 30 minutes of flight time, the pilot notices that, due to the wind, the plane has actually traveled 80 km at an angle 5° east of North.

(a) What is the wind velocity?

(b) In what direction should the pilot have headed to reach the intended destination?

Solution to (a)

We consider velocity vectors for the plane and the wind.

Let vi be the initial, intended velocity for the plane and vg the actual velocity relative to the ground.

If w is the velocity of the wind, v_g is the resultant, that is, the vector sum v_i + w as shown in the figure.

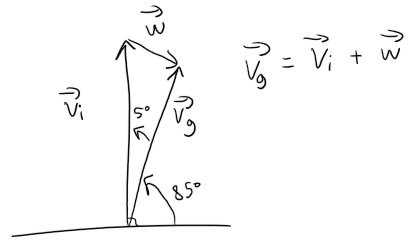
We know that v_i = 180 j (due North), and since the plane flew 80 km in 1/2 hour, |v_g| = 160 km/h.

Thus we have:

Calculation Check:

160 * cos(85) = 13.9449188396253
160 * sin(85) = 159.3911516946793

Now we can solve for the wind velocity.

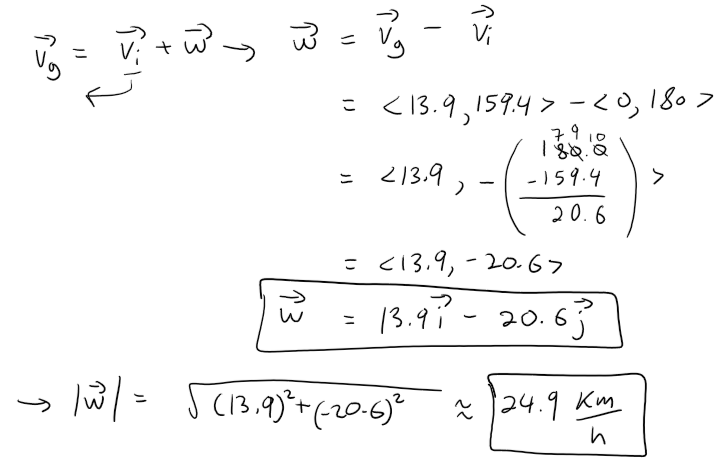
Calculation Check:

sqrt(13.9^2 + (-20.6)^2) = 24.85095571602831
159.4 - 180 = -20.6

Solution to (b)

Let v be the velocity the pilot should have taken.

The pilot would need to head a little west of north to compensate for the wind, so let θ be the angle v makes with the north direction.

With the effect of the wind, the actual velocity (with respect to the ground) will be v + w, which we want to be due north.

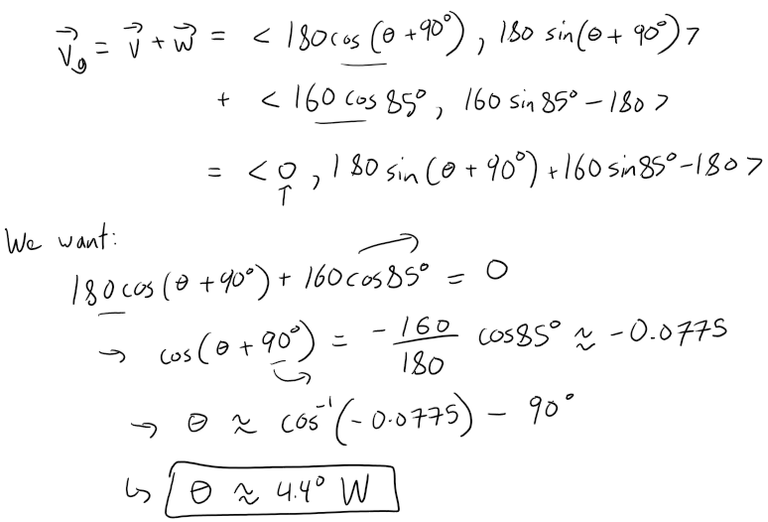
Thus the pilot should have headed about 4.4° west of north.

Calculation Check:

-160/180 * cos(85) = -0.0774717713312517
acos(-160/180*cos(85)) - 90 = 4.443257756886709

180 * sin(4.4+90)+160 * sin(85)-180 = 158.860647095525

The final ground speed is approximately 158.9 km/h, which is a bit slower than the previous 160 km/h because this time we are heading more head on against the wind.

---

Problem 5: Sum of vector projections

Suppose v₁ and v₂ are vectors with |v₁| = 2, |v₂| = 3, and v₁∙v₂ = 5.

Let v₃ = proj_v1v₂, v₄ = proj_v2v₃, v₅ = proj_v3v₄, and so on.

Compute ∑^∞_n=1 |v_n|

Solution:

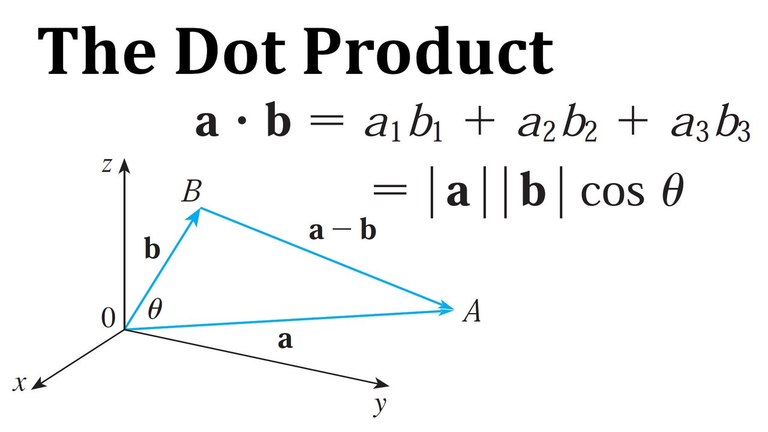
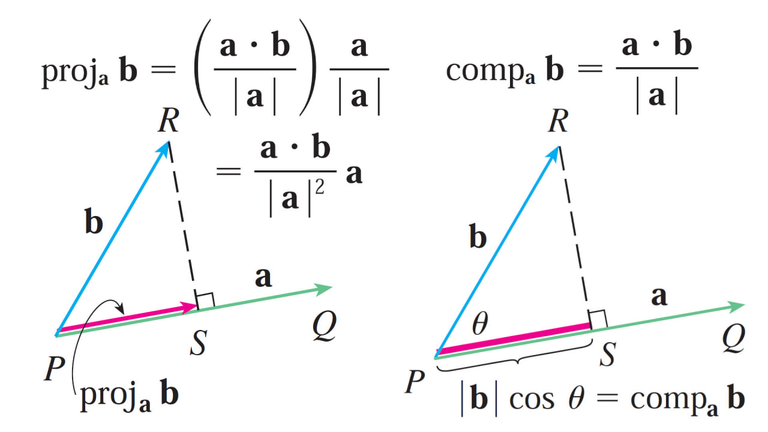
Recall the Dot Product and vector projections:

Let's calculate out the projections and try to find a pattern.

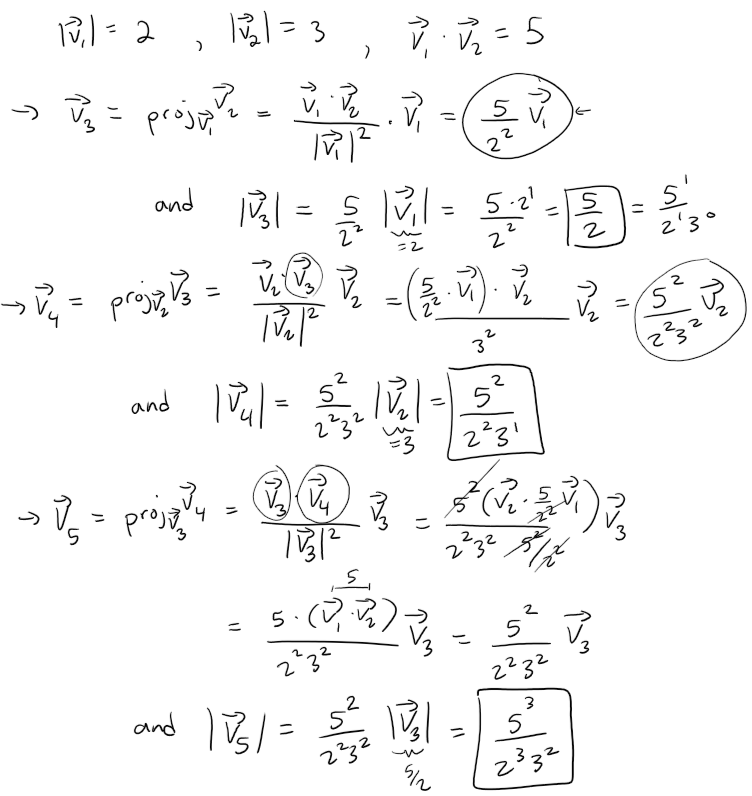
Recall the Sum of the Geometric Series formula I used.

Problem 6: Largest sphere in a sphere

Find an equation of the largest sphere that passes through the point Q(-1, 1, 4) and is such that each of the points (x, y, z) inside the sphere satisfies the condition:

x² + y² + z² < 136 + 2(x + 2y + 3z)

Solution:

Let's complete all the squares first.

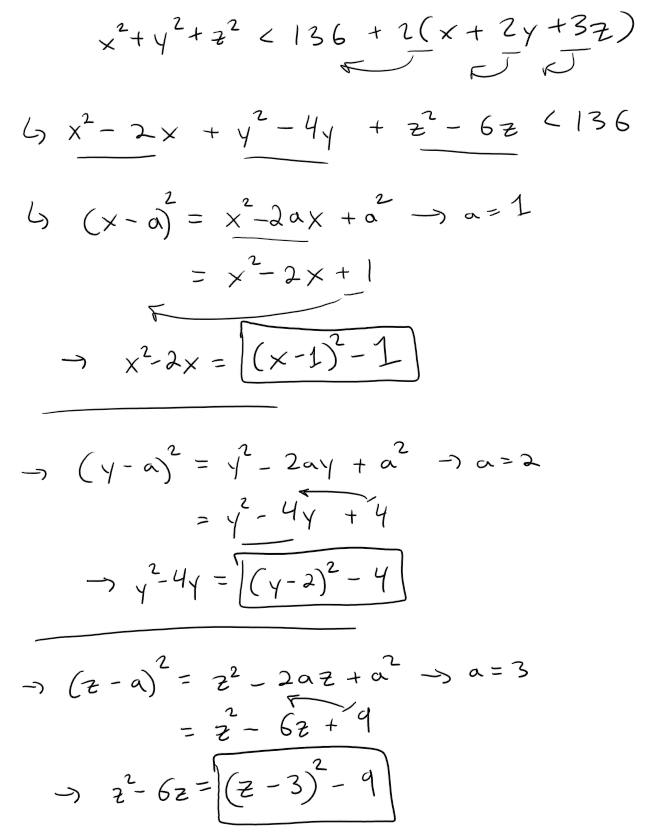
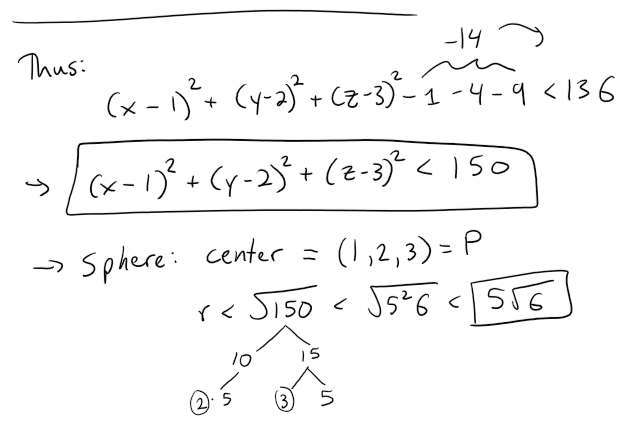
This is a sphere which describes the set of all points (x, y, z) whose distance from the point P(1, 2, 3) is less than 5(61/2).

The distance from P to Q(-1, 1, 4) is:

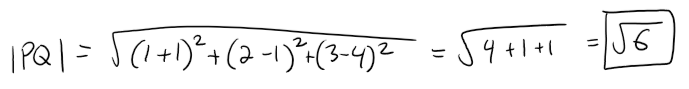
Thus the largest possible sphere that passes through Q and satisfies the stated conditions extends 5(6^1/2) units in the opposite direction, giving a diameter of 6(6^1/2), as in the diagram below.

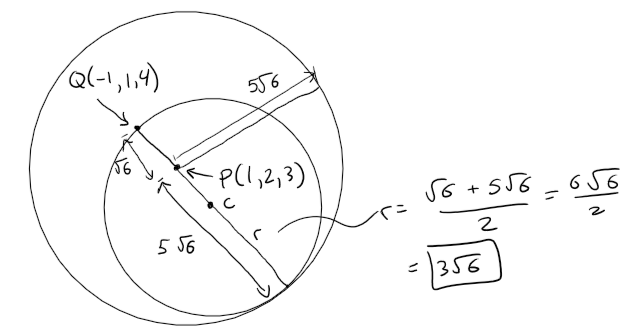
Thus the radius of the desired sphere is 3(6^1/2), and its center is 3(6^1/2) units from Q in the direction of P.

We can use a unit vector in this direction, but first recall unit vectors.

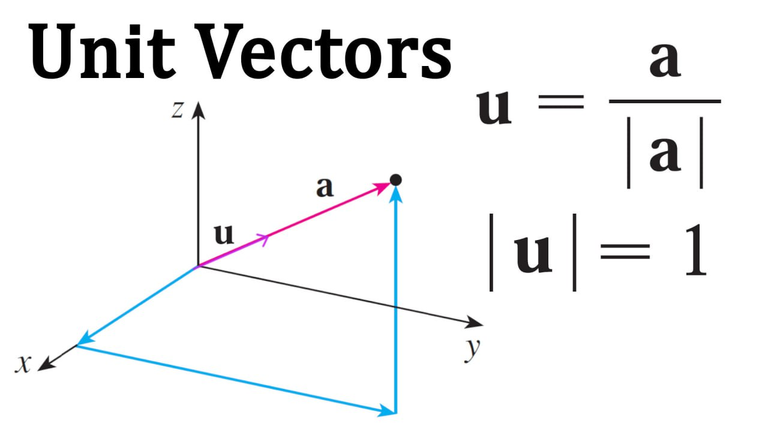
Thus a unit vector in the direction from Q to P is:

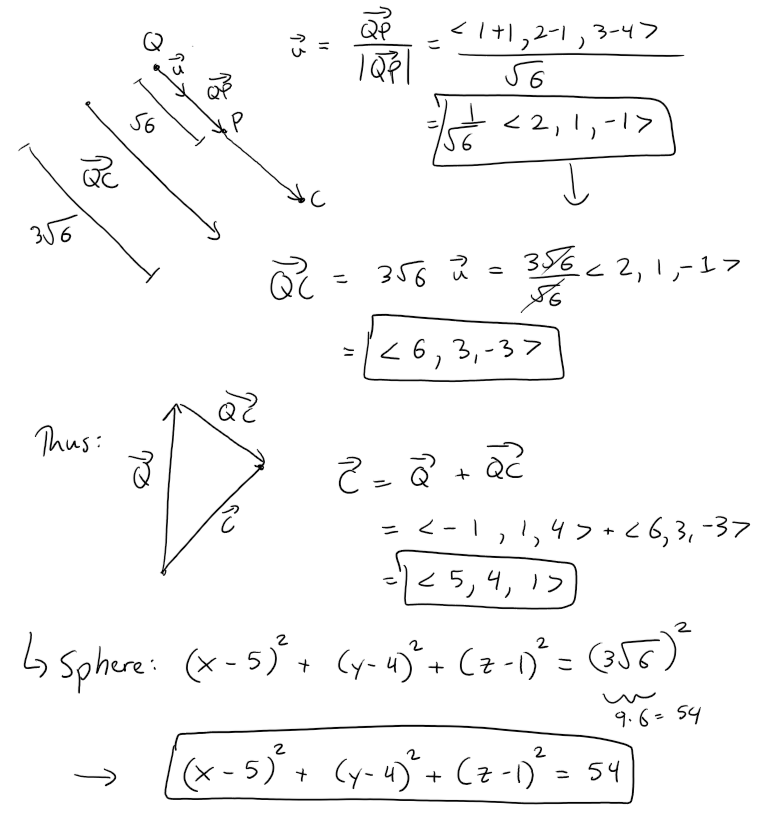
This is the largest sphere under the conditions of the question.

We can graph this using GeoGebra: https://www.geogebra.org/3d/dtdpukqs

---

Problem 7: Block on an inclined plane

Suppose a block of mass m is placed on an inclined plane, as shown in the figure below.

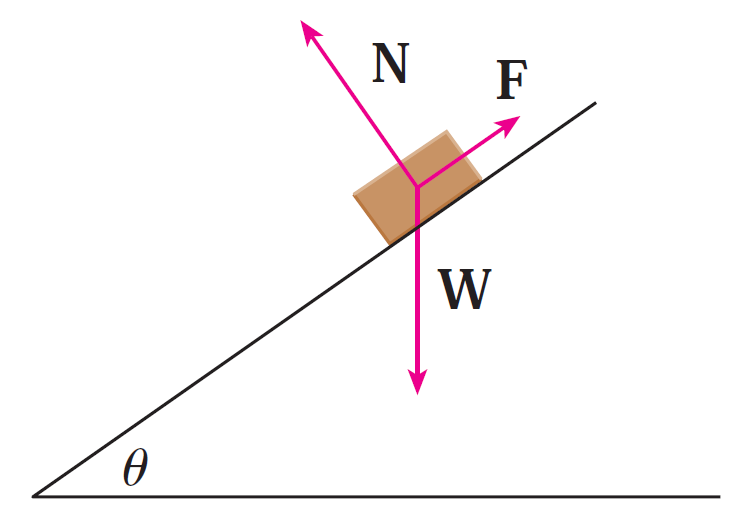
The block's descent down the plane is slowed by friction; if θ is not too large, friction will prevent the block from moving at all.

The forces acting on the block are the weight W, where |W| = mg (g is the acceleration due to gravity); the normal force N (the normal component of the reactionary force of the plane on the block), where |N| = n; and the force F due to friction, which acts parallel to the inclined plane, opposing the direction of the motion.

If the block is at rest and θ is increased, |F| must also increase until ultimately |F| reaches its maximum, beyond which the block begins to slide.

At this angle θ_s, it has been observed that |F| is proportional to n.

Thus, when |F| is maximal, we can say that |F| = µ_sn, where µ_s is called the coefficient of static friction and depends on the materials that are in contact.

(a) Observe that N + F + W = 0 and deduce that µs = tan(θ_s).

(b) Suppose that, for θ > θ_s, an additional outside force H is applied to the block, horizontally from the left, and let |H| = h.

If h is small, the block may still slide down the plane; if h is large enough, the block will move up the plane.

Let h_min be the smallest value of h that allows the block to remain motionless (so that |F| is maximal).

By choosing the coordinate axes so that F lies along the x-axis, resolve each force into components parallel and perpendicular to the inclined plane and show that:

h_minsinθ + mg∙cosθ = n and h_mincosθ + µ_sn = mg∙sinθ

(c) Show that:

h_min = mg∙tan(θ - θ_s)

Does this equation seem reasonable?

Does it make sense for θ = θ_s? As θ → 90°? Explain.

(d) Let hmax be the largest value of h that allows the block to remain motionless.

In which direction is F heading?

Show that:

h_max = mg∙tan(θ + θ_s)

Does this equation seem reasonable? Explain.

Solution to (a)

When θ = θ_s, the block is not moving, so the sum of the forces on the block must be 0, thus: N + F + W = 0.

This relationship is illustrated geometrically in the figure below.

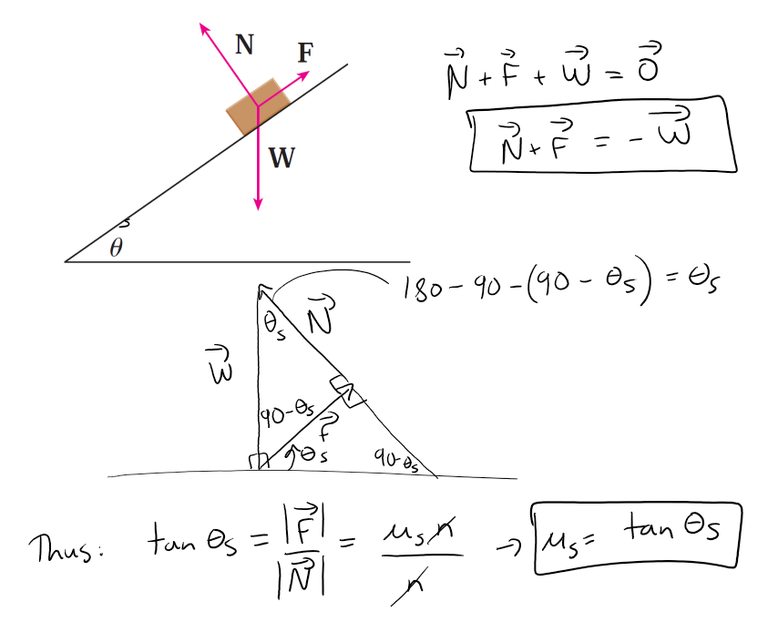
Solution to (b)

We place the block at the origin and sketch the force vectors acting on the block including the additional horizontal force H, with initial points at the origin.

We then rotate this system so that F lies along the positive x-axis and the inclined plane is parallel to the x-axis, as in the following figure.

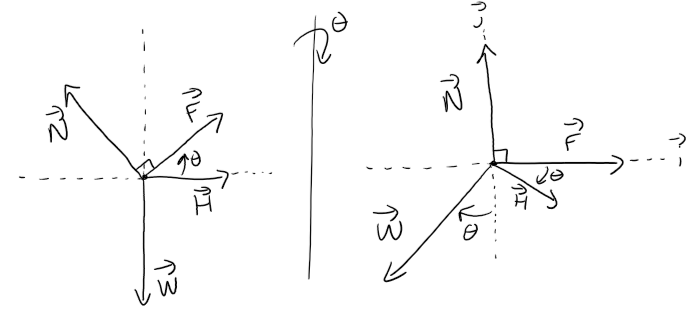
|F| is maximal, so |F| = µ_sn for θ > θ_s.

Then the vectors, in terms of components parallel and perpendicular to the inclined plane, are:

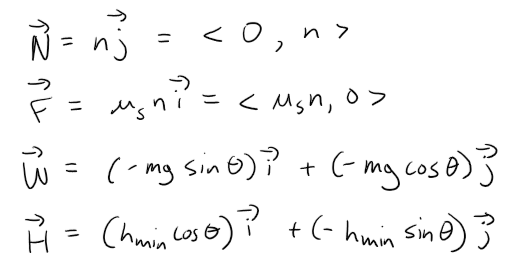
Equating components, we have:

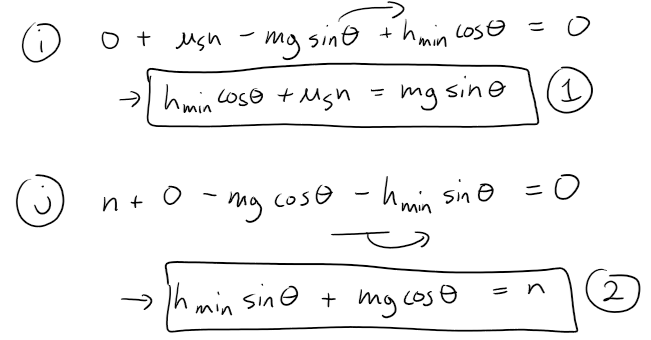
Solution to (c)

Since Equation 2 is solved for n, we can substitute it into Equation 1.

Note the trigonometric identity I used:

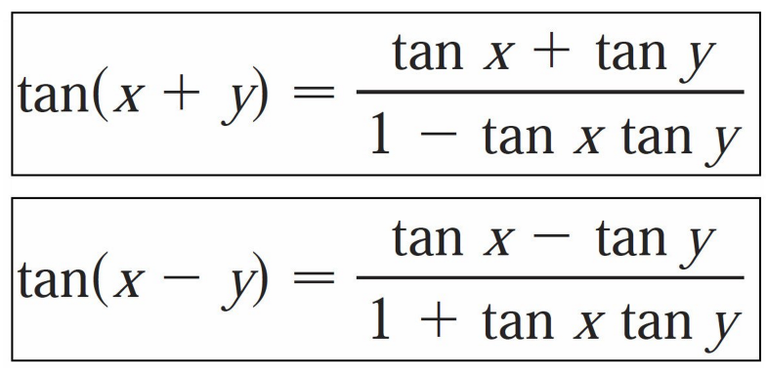
Note that for θ = θ_s, h_min = mg tan 0 = 0, which makes sense since the block is at rest for θ_s, thus no additional force H is necessary to prevent it from moving.

As θ increases, the factor tan(θ - θ_s), and hence the value of h_min, increases slowly for small values of θ - θ_s but much more rapidly as θ - θ_s becomes significant.

This seems reasonable, as the steeper the inclined plane, the less the horizontal components of the various forces affect the movement of the block, so we need a much larger magnitude of horizontal force to keep the block motionless.

If we allow θ → 90°, corresponding to the inclined plane being placed vertically, the value of hmin is quite large; this is to be expected, as it takes a great amount of horizontal force to keep an object from moving vertically.

In fact, without friction (so θ_s = 0), we would have θ → 90° and thus h_min → ∞, and it would be impossible to keep the block from slipping.

Solution to (d)

Since h_max is the largest value of h that keeps the block from slipping, the force of friction is keeping the block from moving up the inclined plane; thus, F is directed down the plane.

Our system of forces is similar to that in part (b), then, except that we have the friction force F = -(µ_sn)i.

Note that |F| is again maximal.

Following our procedure in parts (b) and (c), we can equate components:

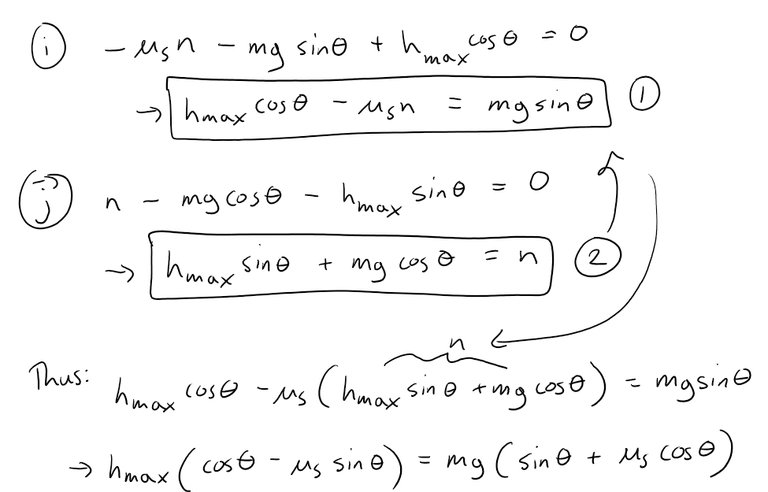
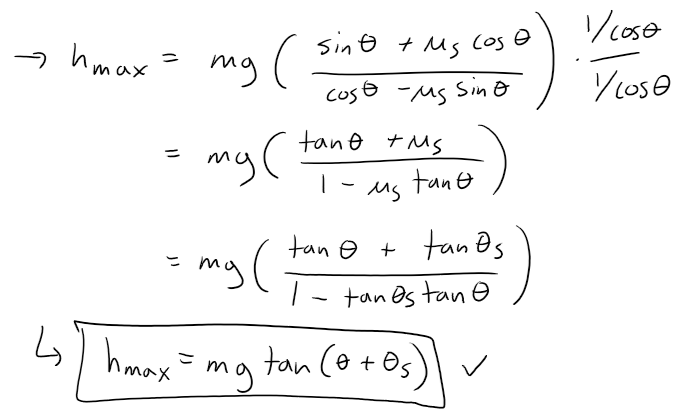
We would expect h_max to increase as θ increases, with similar behavior as we established for h_min, but with h_max values larger than h_min.

We can see this is the case if we graph h_max as a function of θ, as the curve is the graph of h_min translated 2θ_s to the left, so the equation does seem reasonable.

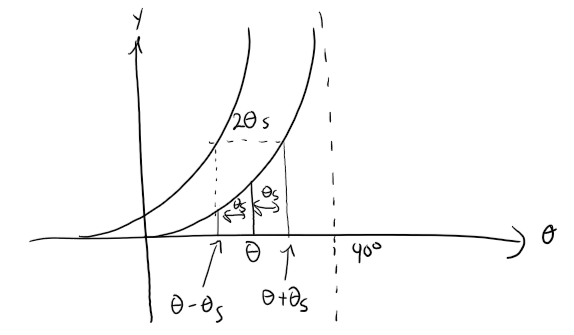
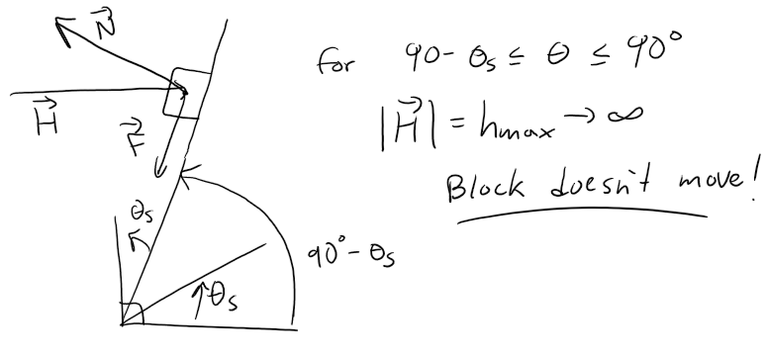
Notice that the equation predicts h_max → ∞ as θ → (90° - θ_s).

In fact, as h_max increases, the normal force increases as well.

When (90° - θ_s) ≤ θ ≤ 90° , the horizontal force is completely counteracted by the sum of the normal and friction forces, so no part of the horizontal force contributes to moving the block up the plane no matter how large its magnitude.

---

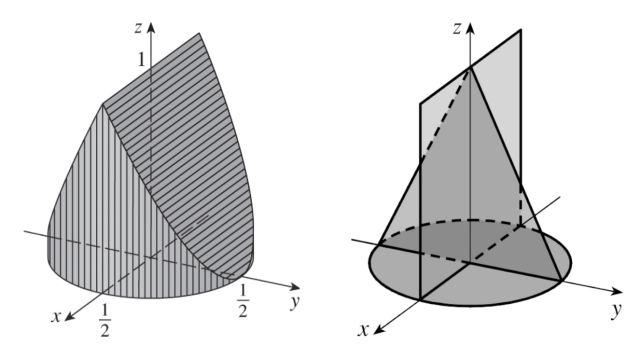
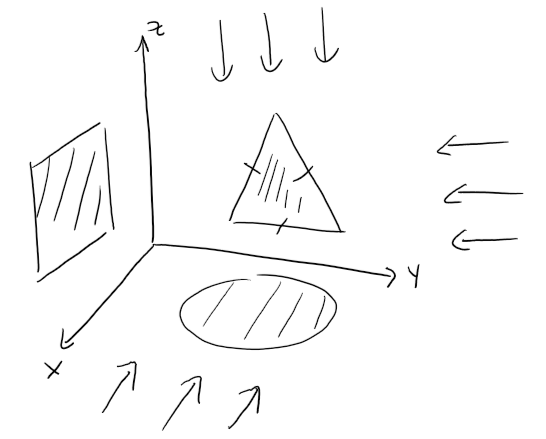
Problem 8: Volume of a solid from its shadows

A solid has the following properties.

When illuminated by rays parallel to the z-axis, its shadow is a circular disk.

If the rays are parallel to the y-axis, its shadow is a square.

If the rays are parallel to the x-axis, its shadow is an isosceles triangle.

In Exercise 44 in Section 12.1 (of my Calculus Book) you were asked to describe and sketch an example of such a solid, but there are many such solids.

Assume the projection onto the xz-plane is a square whose sides have length 1.

(a) What is the volume of the largest such solid?

(b) Is there a smallest volume?

Solution to (a)

Let's first draw our shadows.

The largest possible solid with these shadows is achieved by starting with a circular cylinder of diameter 1 with axis being the z-axis and with a height of 1.

This is the largest solid that creates a square shadow with side length 1 in the y-direction and a circular disk shadow in the z-direction.

For convenience, we place the base of the cylinder on the xy-plane so that it intersects the x and y-axes at ±1/2.

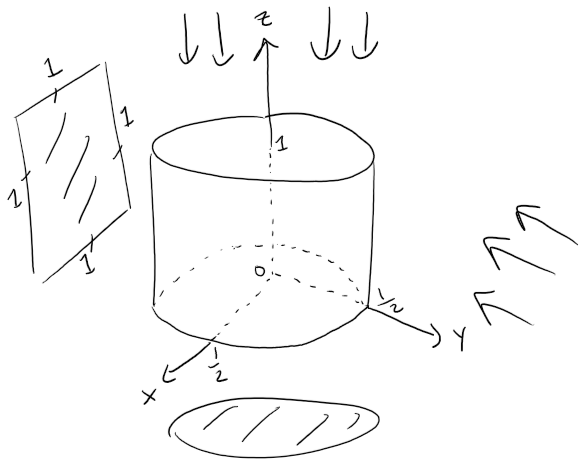
We then remove as little as possible from the solid that leaves an isosceles triangle shadow in the x-direction.

This is achieved by cutting the solid with planes parallel to the x-axis that intersect the z-axis at 1 and the y-axis at ±1/2, as in the figure below.

To compute the volume of this solid, we can take vertical slices parallel to the xz-plane.

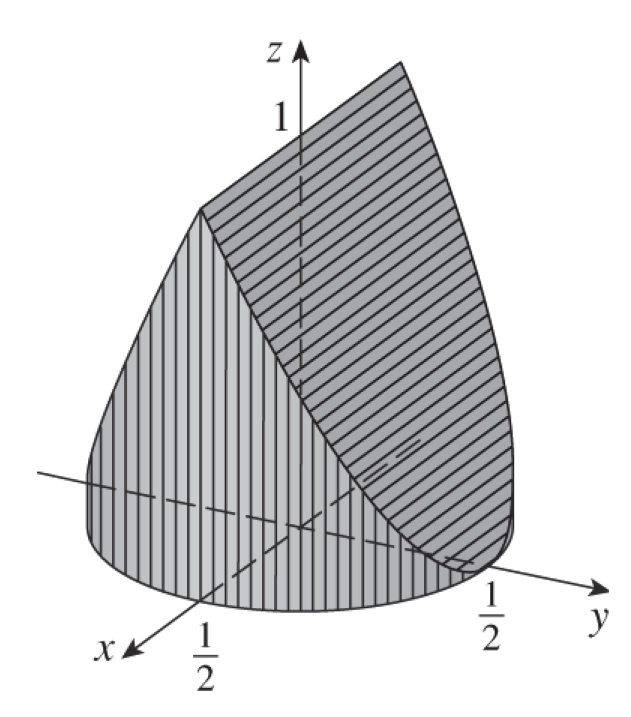
The equation of the base of the solid is the circle with radius 1/2, thus we can obtain the length of a cross section of the solid to the right of the origin.

We can also obtain the height as a function of y and thus the area of the cross section.

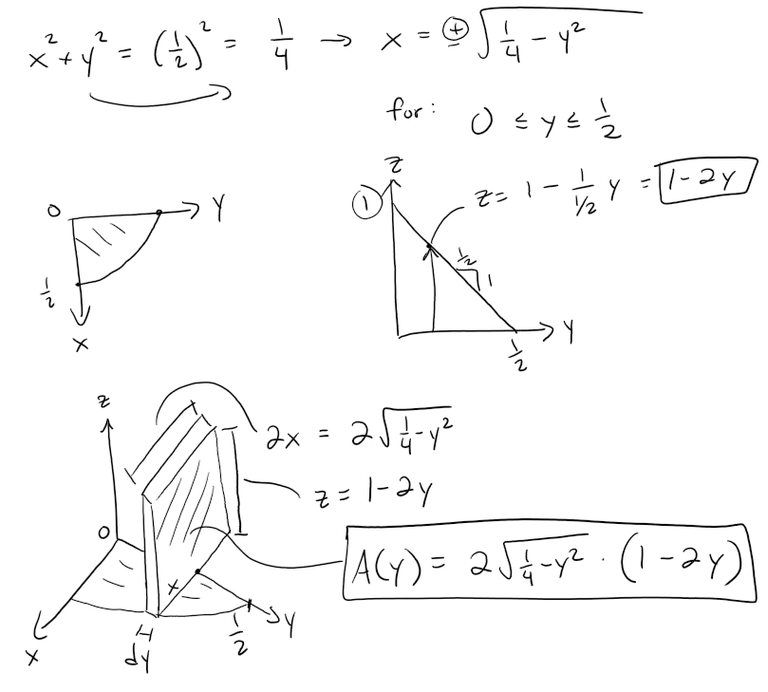
We can now solve the volume of the solid by taking an integral, and multiplying by 2 because of symmetry:

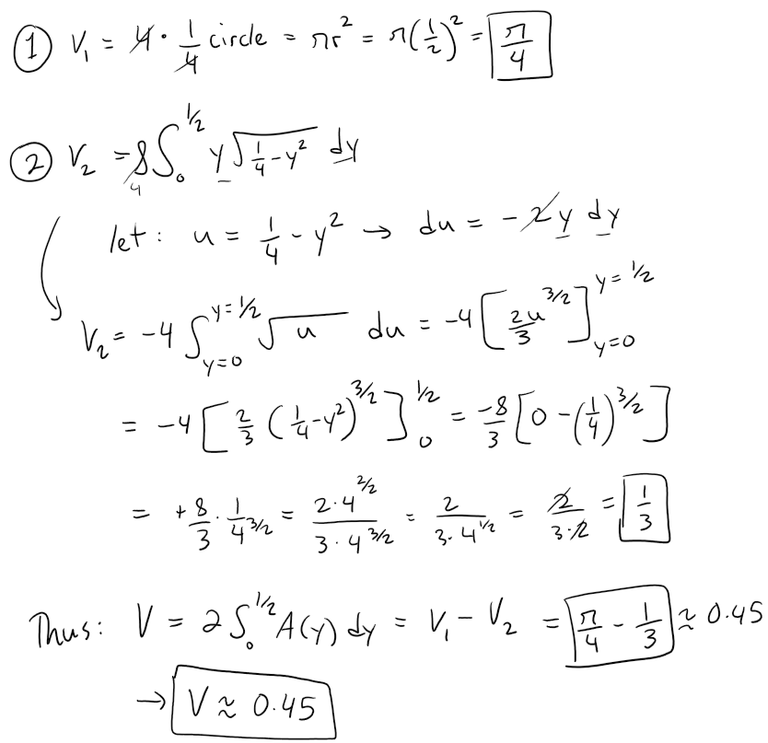
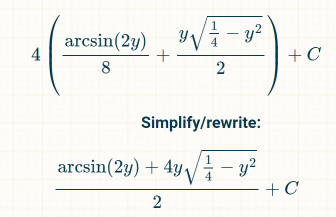
Calculation Check:

https://www.integral-calculator.com/#expr=4sqrt%281%2F4-y%5E2%29&intvar=y&lbound=0&ubound=1%2F2

https://www.integral-calculator.com/#expr=8ysqrt%281%2F4-y%5E2%29&intvar=y&lbound=0&ubound=1%2F2

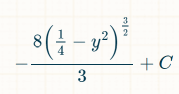
pi/4 - 1/3 = 0.452064830064115

Solution to (b)

There is not a smallest volume.

We can remove portions of the solid from part (a) to create smaller and smaller volumes as long as we leave the "skeleton" shown in the figure intact (which has no volume at all and is not a solid).

Thus we can create solids with arbitrarily small volume.