Cubic Formula Proof Step 1: Removing x^2 term via PQ Substitution

mes in #hive-128780 • 4 days ago

▶️ Watch on 3Speak

In this video I go over the first step in deriving the Cubic Formula, which is to eliminate the x² term from the Cubic Equation by using the PQ Substitution method. This allows us to later apply Vieta's substitution to obtain a quadratic formula, which we can solve. As in the PQ Quadratic Formula method, I set x = y + k and then expand the powers and select a k value such that the x² terms get eliminated. Then rearranging and defining p and q as the terms for the coefficients of the x¹ and x⁰, we obtain the PQ version of the Cubic Equation.

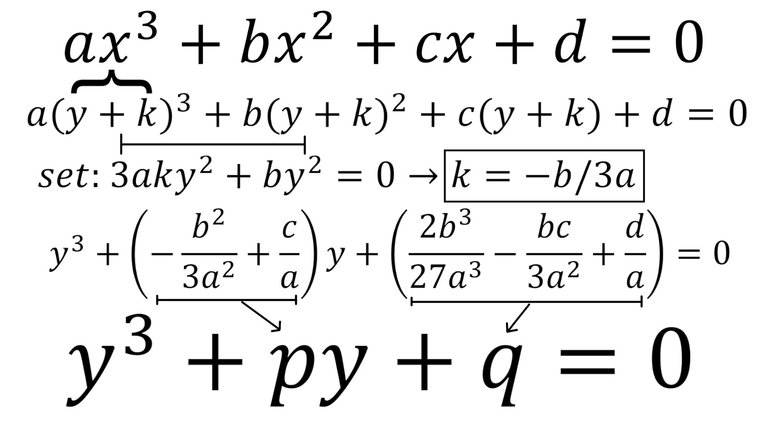
2 Step 1 Remove Square Power PQ.jpeg

Time stamps

Step 1: Get rid of x² term using PQ Substitution in order to later apply Vieta's substitution to get a quadratic formula: 0:00
Applying PQ substitution to cubic equation by letting x = y + k: 1:46
Expanding out the y² terms only: 3:20
Equate y² terms to equal zero and solve for k: 5:10
Recap of Pascal's Triangle: https://en.wikipedia.org/wiki/Pascal%27s_triangle 6:00
Plugging in our k to cancel out terms and rearrange equation: 7:43
Divide new Cubic Equation by a: 13:40
Substitute p and k to obtain the new PQ Cubic Equation: 14:45

Notes and playlists

Summary: https://peakd.com/hive-128780/@mes/wwtmttrs
Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0EF05ExjzLbB64NgUjoV1hl
Notes: https://peakd.com/hive-128780/@mes/dzekfnxh .

Become a MES Super Fan! https://www.youtube.com/channel/UCUUBq1GPBvvGNz7dpgO14Ow/join

DONATE! ʕ •ᴥ•ʔ https://mes.fm/donate

SUBSCRIBE via EMAIL: https://mes.fm/subscribe

MES Links: https://mes.fm/links

MES Truth: https://mes.fm/truth
Official Website: https://MES.fm
Hive: https://peakd.com/@mes

Email me: contact@mes.fm

Free Calculators: https://mes.fm/calculators

BMI Calculator: https://bmicalculator.mes.fm
Grade Calculator: https://gradecalculator.mes.fm
Mortgage Calculator: https://mortgagecalculator.mes.fm
Percentage Calculator: https://percentagecalculator.mes.fm

Free Online Tools: https://mes.fm/tools

iPhone and Android Apps: https://mes.fm/mobile-apps

▶️ 3Speak

#math #science #education #stemgeeks #chessbrothers #stemsocial #palnet #proofofbrain #algebra #mathematics

Sort:

mes 4 days ago

!summarize

conscript 4 days ago

You don't have an active Creator Subscription to @mightpossibly. Subscribe for immediate access

mes 3 days ago

!summarize

conscript 3 days ago

You don't have an active Creator Subscription to @mightpossibly. Subscribe for immediate access

mes 3 days ago

@mightpossibly I keep getting this error, even though I continued my subscription 7 hours ago. Would you know why?

mightpossibly 3 days ago

Ahh, something is definitely not working correctly with this. Apologies, I will look into it. Your sub is active now and I added a couple of days for your trouble

mes 3 days ago

Amazing thanks! Yeah hopefully it gets fixed up.

mes 4 days ago

!summarize

conscript 4 days ago

You don't have an active Creator Subscription to @mightpossibly. Subscribe for immediate access

mes 3 days ago

!summarize

ai-summaries 3 days ago

Part 1/5:

Understanding the PQ Substitution Method for Cubic Functions

The process of solving cubic equations can often seem daunting, especially when you come across terms that complicate the equation, like the (x^2) term. However, one effective method known as the PQ Substitution Method aids in simplifying and solving these cubic functions, allowing for greater clarity and ease in finding solutions.

The Aim of PQ Substitution

The primary goal in using the PQ substitution method is to eliminate the (x^2) term in a cubic function. When we have a general cubic equation structured as:

[

a x^3 + b x^2 + c x + d = 0

]

ai-summaries 3 days ago

Part 2/5:

we will manipulate this equation by substituting (x) with a new variable adjustment, ultimately transitioning to a form manageable with quadratic formulas. This approach opens the door to simplification and ultimately solving the cubic equation using techniques similar to those employed in quadratic equations.

Applying the PQ Substitution Method

Step 1: Restructuring the Variable

We initiate this process by letting:

[

x = y + k

]

This substitution is aimed at removing the (x^2) term. After applying this substitution to the original cubic equation, we expand it leading us to new expressions for each term—especially focusing on how to set (k) in a way that ensures the elimination of (y^2).

Step 2: Choosing (k) to Cancel Out (y^2)

ai-summaries 3 days ago

Part 3/5:

To effectively cancel out all appearances of (y^2), we identify the contributions each expanded term provides. Upon careful arrangement and addition of the coefficients of (y^2), we ultimately derive the value of (k):

[

k = \frac{b}{3a}

]

This manipulation is crucial, as it allows all (y^2) terms to sum to zero in our transformed equation.

Moving Forward with Expanded Functions

After substituting (k) back into our cubic function, our equations begin to take on a new shape. It becomes paramount to expand these functions systematically, employing tools like Pascal's Triangle to aid in accurately managing the coefficients during binomial expansions.

Understanding Coefficients Using Pascal's Triangle

ai-summaries 3 days ago

Part 4/5:

Pascal's Triangle plays a significant role in understanding the connections between coefficients in polynomial expansions. For instance:

The coefficients for ((x + 1)^2) are (1, 2, 1).
The coefficients for ((x + 1)^3) are (1, 3, 3, 1).

These coefficients track with the pattern in the triangle, allowing us to predict outcomes without manual expansion.

Final Transformation

With all the pieces in place, we now systematically replace (k) into our expanded cubic equation. Each component must be collected, and discrepancies in (y^2) terms should be canceled. Once completed, the focus should shift to isolating (y^3):

[

y^3 + p y + q = 0

]

ai-summaries 3 days ago

Part 5/5:

Here, (p) and (q) comprise the collective linear and constant outcomes of our rearranged equation, capturing the essence of our cubic function in a quadratic-like format, which can be solved using familiar quadratic techniques.

Conclusion

The PQ substitution method is a powerful tool for transforming cubic equations into simpler forms that can be tackled using established quadratic formulas. This method, while requiring precision through variable substitution and polynomial expansion, culminates in a streamlined process, allowing easier solutions to otherwise complex cubic equations. By mastering this technique, one can gain significant advantages in understanding and solving the realm of cubic functions.