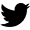Is this prime?
So ich habe Berlin Web3 erfolgreich hinter mich gebracht. Ich bin froh, dass ich dieses Event mitgenommen habe. Dank @alucians und @kikihamster konnte ich auch noch Sonntag miterleben und nicht nur Samstag. Als Bezahlung haben wir uns auf eine Print HiQ geeinigt. 🤪
Ich habe einige Hivians zum 2. Mal getroffen und natürlich auch einige zum 1. Mal. Wie
So I have successfully completed Berlin Web3. I'm glad I took this event with me. Thanks to @alucians and @kikihamster I was also able to experience Sunday and not just Saturday. As payment we agreed on a print HiQ. 🤪
I met some Hivians for the 2nd time and of course some for the 1st time. Like
@flauwy, @broxi, @crimsonclad, @arcange, @elindos, @e-rich1, @detlev, @solarwarrior, @starkerz, @louis88, @rivalzzz, @bastisvlogs, @stortebeker, @gtg
Es waren einige prägende Erinnerungen dabei und wir haben einigen Besuchern der Messe hoffentlich Hive schmackhaft machen können.
Zum Abschied konnte @detlev mit seiner Delegation noch einen BEER Sponsor auftreiben. Grund genug für uns einen #beersaturday am Sonntag zu veranstalten.
Nach dem BEER pilgerten einige von uns noch zu McDonald's. Auch wenn ich nur sehr widerwillig mit bin. Ich war bewusst bestimmt schon über 10 Jahre nicht mehr bei McDonald's, LOOL. Bei der Bestellung bekamen wir alle eine Wartenummer. Als ich klagend anmerkte, dass meine 175 keine Primzahl ist, entgegnete @solarwarrior, dass er eine Primzahl hat - 173.
There were some formative memories and hopefully we were able to make Hive palatable to some visitors of the fair.
As a farewell, @detlev and his delegation were able to find a BEER sponsor. Reason enough for us to have a #beersaturday on Sunday.
After the BEER, some of us made a pilgrimage to McDonald's. Even though I was very reluctant to go. I'm sure I haven't been to McDonald's for over 10 years, LOOL. When we ordered, we were all given a waiting number. When I complained that my 175 was not a prime number, @solarwarrior replied that he had a prime number - 173.
Nun musste ich doch dank BEER etwa eine halbe Minute drüber nachdenken. BEER ist auch keine gute Droge für Zahlentheorie. Das ist eher was für Stochastik, LOOL. Wie dem auch sei. Dank dem Primzahlsieb von Eratosthenes und einer Prise Zahlentheorie weiß ich natürlich, dass es ausreicht die Primteiler zu überprüfen, die kleiner sind als die Quadratwurzel aus 173.
Da 132 = 169 < 173 und 172 = (20-3)2 = 400-120+9=289 > 173 (sry wusste gerade 172 nicht auswendig. Aber so sind binomische Formeln auch an einem Beersaturday mal nützlich. LOOL). Folglich kommen als Primteiler von 173 nur 2, 3, 5, 7 und 11 in Frage.
Jetzt checken wir das noch kurz. 2 ist kein Teiler, da 173 ungerade ist. 5 ist kein Teil, da 173 nicht 175 ist, LOOL. 3 ist kein Teiler, da die Quersumme von 173 11 ist und 11 ist nicht durch 3 teilbar. 11 ist kein Teiler von 173, da die alternierende Quersumme, nennen wir sie AQS, nicht 0 ist. (AQS(11) = 1-7+3 = -3)
Ok, das war easy. Jetzt fehlt nur noch die 7. 173 = -2 = 5 mod 7. Dies ist ungleich 0. Also ist auch 7 kein Teiler von 173. Offensichtlich ist 173 also eine Primzahl. Das hat mich ca. eine halbe Minute gekostet. Aber wie lange hat dies @solarworrior gekostet?
Mit diesen Cliffhanger entlasse ich euch jetzt. Falls ihr mehr wissen wollt, dann müsst ihr euch bis Donnerstag gedulden, denn auf @hiq.redaktion erfahrt ihr mehr.
PS: Und danke an @moneyfox für das BEER.
Well, I had to think about it for half a minute thanks to BEER. BEER is also not a good drug for number theory. It's more for stochastic, LOOL. Anyway. Thanks to Eratosthenes' prime number sieve and a pinch of number theory, I know of course that it is enough to check the prime divisors that are smaller than the square root of 173.
Since 132= 169 < 173 and 172 = (20-3)2 = 400-120+9=289 > 173 (sry, I didn't know 172 by heart just now. But so the binomial formula are also useful on a Beersaturday. LOOL). Consequently, only 2, 3, 5, 7 and 11 are possible prime divisors of 173.
Now let's check this for a moment. 2 is not a divisor because 173 is odd. 5 is not a divisor because 173 is not 175, LOOL. 3 is not a divisor because the sum of the digits of 173 equals 11 and 11 is not divisible by 3. 11 is not a divisor of 173 because the alternating sum of the digits, let's call it ASotD, is not 0. (ASotD(11) = 1-7+3 = -3)
Ok, that was easy. Now only 7 is missing. 173 = -2 = 5 mod 7. This is not equal to 0. So 7 is also not a divisor of 173. Obviously 173 is a prime number. That took me about half a minute. But how long did this cost @solarwarrior?
With that cliffhanger, I'll let you go now. If you want to know more, you'll have to wait until Thursday, because you can find out more on @hiq.redaktion.
PS: And thanks to @moneyfox for the BEER.