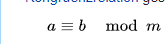created with bingGPT. LOOL
Das Ergebnis von 1 durch 7
Es ist mal wieder Zeit für einen Mathe-Post. Dieser Post soll sich wie die Überschrift hoffentlich schon verrät, um das Ergebnis von 1 durch 7 drehen. Jetzt denkt sich vielleicht der eine oder andere Leser, der in der Schule aufgepasst hat und der Bruchrechnung einigermaßen mächtig ist: "Was soll daran so besonders sein?"
Wenn man sich aber ein wenig mit dem Thema auseinander setzt, stellt man fest, dass überraschend viel Mathematik dahinter steckt. 1/7 ist erst mal ein Bruch. Wir könnten jetzt auf die Idee kommen diesen Bruch in eine Dezimalzahl umzuwandeln. Dafür könnte man zum Beispiel schriftliche Division verwenden. (Sagt bloß nicht zu frühpubertierenden Schwanzrechnung, LOOL.)
0.142857142857142857....
Die Sequenz von 142857 scheint sich immer wieder zu wiederholen. Wir nennen sowas eine Periode. Periodische Dezimalzahlen sind euch bestimmt schon öfter begegnet. Wir könnten uns jetzt einfach damit zufrieden geben oder wir könnten uns auch krasse Fragen stellen. Natürlich machen wir das Zweitere.
- Wann treten periodische Dezimalzahlen auf?
- Wie lang wird ihre Periode sein und können wir die Periodenlänge vorhersehen?
Die erste Frage ist recht leicht zu beantworten. Die zweite Frage eher nicht so und genau diese wird auch interessant werden.
Haben wir einen Bruch der Form a/10n, dann lässt sich dieser sehr leicht in eine endliche Dezimalzahl überführen. Zum Beispiel ist 142857/10000000=0.142857. LOOL
Folglich sind solche Brüche immer endliche Dezimahlzahlen. Aber es gibt auch andere Nenner, die keine Perioden erzeugen. Wann aber bekommen wir eine Periode?
In der Schule wird gerne zwischen gemischt-periodischen und rein-periodische Brüchen unterschieden. Welchen der 3 Fälle man vor sich hat, erkennt man an den Primteilern des Nenners. Hat der Nenner nur die Primteile 2 und/oder 5, dann bekommen wir eine endliche Dezimalzahl. Hat der Nenner weder die 2 noch die 5 als Primteiler, ist die Dezimalzahl rein-periodisch. Und haben wir neben 2 und/oder 5 noch andere Primteiler, bekommen wir eine gemischt-periodische Dezimalzahl.
Um uns jetzt der 2. Frage etwas annähern zu können, brauchen wir etwas Gruppentheorie. Da man das in der Schule nicht hat, werde ich ein wenig über Gruppen schwurbeln. Erst mal haben wir eine Menge. In der Regel sind in dieser Menge Zahlen drin. Es müssen aber keine Zahlen in der Menge sein. In einer Menge könnten auch andere Dinge sein wie Matrizen, Punkte, Funktionen und was nicht noch so alles schönes gibt. Die Menge könnte endlich oder unendlich sein. Wir werden mit Mengen zu tun haben, die endlich sind und es sind auch Zahlen drin. (Müssten es aber nicht, LOOL.)
Unsere Menge G hat jetzt noch eine Rechnenoperation ·. Im folgenden mit (G, ·) benannt. Die Rechenoperation sieht zwar zum verwecheln ähnlich aus zur Multiplikation, es könnte aber auch eine völlig andere Operation sein. (G, ·) muss verschiedene Eigenschaften erfüllen, damit es eine Gruppe ist - sogenannte Axiome. Damit wir auf der Gruppe rechnen können, muss unsere Gruppe immer abgeschlossen bezüglich der Rechenoperation sein. D.h. die Ergebnis einer jeden Rechnung muss wieder in der Gruppe sein. (G, ·) muss außerdem folgende Axiome erfüllen, um sich eine Gruppe nennen zu dürfen:
- Existenz eines neutralen Elementes
- Existenz eines Inversen Elementes
- Assoziativgesetzt
- Kommutativitätsgesetz
Das 4. Gesetzt ist genaugenommen kein Gruppenaxiom. Gilt nämlich zusätzlich das 4. Gesetz, handelt es sich um eine abelsche oder kommutative Gruppe. Wir wollen uns nun folgendes Beispiel reinziehen. Sei G={1,2,3,4,5,6} und sei sei die Rechenoperation die Multiplikation Modulo 7. Die Multiplikationtafel würde nun wie folgt aussehen:
| · | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 3 | 6 | 2 | 5 | 1 | 3 |
| 4 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 6 | 5 | 4 | 3 | 2 | 1 |
Wie wir durch Ausprobieren aller möglichen Multiplikationen sehen können, ist die Multiplikation Modulo 7 abgeschlossen, da es nur die Ergebnisse 1, 2, 3, 4, 5, 6 gibt. Wer Modulorechnung nicht kennt, es handelt sich um Teilen mit Rest, wo nur die Reste als Ergebnis rauskommen. Zum Beispiel ist 5·5=25=4 mod 7.
Das neutrale Element ist hier die 1, da es das Ergebnis nicht beeinflusst. Inverse Elemente erkennt man daran, dass als Ergebnis das neutrale Element, d.h. 1, raus kommt. Zum Beispiel gilt 3·5=15=1 mod 7. Also ist das Inverse zu 3 die 5. (Und umgekehrt.) Wenn jedes Element ein Inverses besitzt, ist dieses Gruppenaxiom erfüllt. Das Assoziativ gesetzt gilt hier auch. Das werden wir aber nicht nachprüfen. Auch das Kommutativgesetzt gilt hier. Beide Gesetze folgen übrigens daraus, dass wir hier Modulo rechnen.
Nun können Gruppen noch eine Ordnung haben. Unsere Gruppe hat die Ordnung 6, da G={1,2,3,4,5,6} 6 Elemente hat. 1/7=0.142857... hat die Periodenlänge 6. Zufall?
Sollte der Nenner p eines Bruches eine Primzahl sein, die nicht 2 oder 5 ist, dann ist die größtmögliche Periodenlänge p-1. Man kann natürlich überall noch viel tiefer reingehen. Wir konzentrieren uns hier aber weiter auf 1/7. Wie schon erwähnt erhalten wir eine Dezimaldarstellung von 1/7, wenn wir eine Schwanzrechnung machen.
1:7=0....
Jetzt rechnet man eigentlich 10 durch 7 und notiert sich den Rest. Man rechnet also Modulo 7. (Und ihr dachtet bestimmt der Bogen kommt nie ;)) Und das wiederholen wir nach den Regeln von Adam Riese.
1:7=0.142857...
10
3
30
2
20
6
60
4
40
5
50
1
10
.
.
.
In der Schwanzrechnung habe ich mal die Reste fett markiert. Würden wir jetzt weiter machen, würde sich die Sequenz 142857 einfach immer wiederholen. Man könnte es fast zyklisch nennen. Wie der Zufall so will, gibt es in der Gruppentheorie zyklische Gruppen. Und unsere Gruppe G ist so eine. Eine Gruppe ist dann zyklisch, wenn es mindestens ein Element in dieser Gruppe gibt, was alle Elemente der Gruppe durch Potenzieren erzeugt - die sogenannte Primitivwurzel. Unsere multiplikative Modulo 7 Gruppe G hat bestimmt so eine. Wir versuchen es mal mit der 3.
31=3 mod 7
32=9=2 mod 7
33=27=6 mod 7
34=4 mod 7
35=5 mod 7
36=1 mod 7
.
.
.
Und zack wir haben eine Primitivwurzel gefunden. Und wenn wir unsere Potenzen mal mit den Resten der schriftlichen Division vergleichen, haben wir exakt die gleichen Reste.
Ok, halten wir mal fest, was wir bis hier hin gesammelt haben. Wenn wir einen Bruch der Form 1/p haben und p eine Primzahl ist (außer 2 und 5), dann ist die größtmögliche Periodenlänge p-1. Da man bei der schriftlichen Division immer 10ner-Potenzen durch p teilt, können wir davon ausgehen, dass wir dann die maximale Periodenlänge erhalten, wenn 10 eine Primitivwurzel von der multiplikativen Mopulo p Gruppe ist. Man könnte jetzt noch auf viele weitere Dinge eingehen, aber wir werden uns hier auf Nenner beschränken, die eine Primzahl sind.
Zurück zu unserer 7. 10=3 mod 7. Daher habe ich auch die 3 genommen und geschaut, ob diese eine Primitivwurzel ist. Wie schon amgemerkt, teilt man bei der schriftlichen Division eigentlich 10k durch 7 (oder eine andere Zahl, falls wir einen anderen Nenner hätten).
101=31=3 mod 7
102=32=2 mod 7
103=33=6 mod 7
104=34=4 mod 7
105=35=5 mod 7
106=33=1 mod 7
.
.
.
Wie schon weiter oben erwähnt, ist ein Element der multiplikativen Gruppe eine Primitivwurzel, falls sie durch potenzieren die ganz Gruppe erzeugt. Da 106=33=1 mod 7, ist auch 6 die Ordnung dieser Gruppe. Es ist nämlich das erste k, welches 1 mod p ist, was gerade die Ordnung der Gruppe ist. Und da unsere Gruppe 6 Elemente hat, ist 10=3 mod 7 eine Primitivwurzel von unserer Gruppe.
Wenn 10 eine Primitivwurzel Module p ist, dann haben übrigens alle weiteren Brüche der Form a/p (gekürzt und a darf kein Vielfaches von 7 sein) auch die maximale Periodenlänge und ihre periodische Ziffernfolge ist die gleiche. Sie ist nur zyklisch verschoben.
1/7=0.142857...
2/7=0.285714...
3/7=0.428571...
4/7=0.571428...
5/7=0.714285...
6/7=0.857142...
Meine Schüler habe ich übrigens am letzten Unterrichtstag mit folgenden Lied beglückt: 142857.
Natürlich werde ich sie nach den Ferien gleich fragen, ob sie denn das Ergebnis von 1 durch 7 noch kennen. Und ich hoffe auch ihr werdet es nie vergessen. Es hat sich übrigens auch der Fürst der Mathematik, Karl Friedrich Gauß, sehr ausführlich mit diesen Thema beschäftigt und sogar Tabellen angelegt mit denen man von sehr abgefahrenen Brüchen die Perioden bestimmen konnte. Man bedenke auch, dass er noch keine Computer zur Verfügung hatte.

created with bingGPT. LOOL
The result of 1 divided by 7
It's time for another math post. As the title hopefully already reveals, this post is about the result of 1 divided by 7. Some readers who paid attention at school and have a reasonable grasp of fractions might be thinking: "What's so special about that?"
But if you look into the subject a little, you realize that there is a surprising amount of math behind it. First of all, 1/7 is a fraction. We could now come up with the idea of converting this fraction into a decimal number. For example, we could use written division. (Just don't say anything about early pubescent tail math, LOOL.)
0.142857142857142857....
The sequence of 142857 seems to repeat itself again and again. We call this a period. You've probably come across periodic decimal numbers before. We could just be content with that, or we could ask ourselves some blatant questions. Of course, we'll do the latter.
- when do periodic decimals occur?
- how long will their period be and can we predict the period length?
The first question is quite easy to answer. The second question is not so easy, and this one will also be the interesting one.
If we have a fraction of the form a/10n, then it is very easy to convert it into a finite decimal number. For example is 142857/10000000=0.142857. LOOL
Consequently, such fractions are always finite decimals. But there are also other denominators that do not produce periods. But when do we get a period?
In school, a distinction is often made between mixed-periodic and pure-periodic fractions. Which of the 3 cases you have in front of you can be recognized by the prime divisors of the denominator. If the denominator only has the prime divisors 2 and/or 5, then we get a finite decimal number. If the denominator has neither 2 nor 5 as prime divisors, the decimal number is purely periodic. And if we have other prime divisors in addition to 2 and/or 5, we get a mixed-periodic decimal number.
In order to get a little closer to the second question, we need some group theory. Since you don't have that in school, I'm going to ramble a bit about groups. First of all, we have a set. As a rule, this set contains numbers. But there don't have to be numbers in the set. A set could also contain other things such as matrices, points, functions and all sorts of other things. The set could be finite or infinite. We will be dealing with sets that are finite and there are also numbers in them. (But they don't have to be, LOOL.)
Our set G now has an arithmetic operation ·. Named (G, ·) in the following. Although the arithmetic operation looks confusingly similar to multiplication, it could also be a completely different operation. (G, ·) must fulfill various properties in order to be a group - so-called axioms. So that we can calculate on the group, our group must always be closed with respect to the arithmetic operation. This means that the result of each calculation must be in the group again. (G, ·) must also fulfill the following axioms in order to be called a group:
- existence of a neutral element
- existence of an inverse element
- associative law
- commutativity law
Strictly speaking, the 4th law is not a group axiom. If the 4th law also applies, it is an abelian or commutative group. Let us now consider the following example. Let G={1,2,3,4,5,6} and let the arithmetic operation be the multiplication modulo 7. The multiplication table would now look like this:
| · | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 3 | 6 | 2 | 5 | 1 | 3 |
| 4 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 6 | 5 | 4 | 3 | 2 | 1 |
As we can see by trying out all possible multiplications, the multiplication modulo 7 is complete, as there are only the results 1, 2, 3, 4, 5, 6. For those who are not familiar with modulo arithmetic, this is a division with remainder, where only the remainders come out as the result. For example, 5·5=25=4 mod 7.
The neutral element here is 1, as it does not affect the result. Inverse elements can be recognized by the fact that the result is the neutral element, i.e. 1. For example, 3·5=15=1 mod 7, so the inverse of 3 is 5. (And vice versa.) If every element has an inverse, this group axiom is fulfilled. The associative set also applies here. However, we will not check this. The commutative law also applies here. Incidentally, both laws follow from the fact that we are calculating modulo here.
Now groups can still have an order. Our group has the order 6, since G={1,2,3,4,5,6} has 6 elements. 1/7=0.142857... has a period length of 6. Coincidence?
If the denominator p of a fraction is a prime number that is not 2 or 5, then the largest possible period length is p-1. Of course, you can go much deeper everywhere. However, we will continue to concentrate on 1/7 here. As already mentioned, we get a decimal representation of 1/7 if we do a tail calculation.
1:7=0....
Now you actually divide 10 by 7 and write down the remainder. So you calculate modulo 7 (and you probably thought the arc would never come ;)) And we repeat this according to the rules of Adam Riese.
1:7=0.142857...
10
3
30
2
20
6
60
4
40
5
50
1
10
.
.
.
I have marked the remainders in bold in the tail calculation. If we were to continue now, the sequence 142857 would simply keep repeating itself. You could almost call it cyclic. As luck would have it, there are cyclic groups in group theory. And our group G is one of these. A group is cyclic if there is at least one element in this group that generates all the elements of the group by exponentiation - the so-called primitive root. Our multiplicative modulo 7 group G certainly has one of these. Let's try it with the 3.
31=3 mod 7
32=9=2 mod 7
33=27=6 mod 7
34=4 mod 7
35=5 mod 7
36=1 mod 7
.
.
.
And bang, we have found a primitive root. And if we compare our powers with the remainders of the written division, we have exactly the same remainders.
Ok, let's record what we have gathered so far. If we have a fraction of the form 1/p and p is a prime number (except 2 and 5), then the greatest possible period length is p-1. Since we always divide powers of 10 by p in written division, we can assume that we get the maximum period length if 10 is a primitive root of the multiplicative mopulo p group. We could go into many more things, but we will limit ourselves here to denominators that are prime numbers.
Back to our 7. 10=3 mod 7, so I also took the 3 and looked to see if it was a primitive root. As already noted, in written division you actually divide 10k by 7 (or another number if we had a different denominator).
101=31=3 mod 7
102=32=2 mod 7
103=33=6 mod 7
104=34=4 mod 7
105=35=5 mod 7
106=33=1 mod 7
.
.
.
As already mentioned above, an element of the multiplicative group is a primitive root if it generates the whole group by exponentiation. Since 106=33=1 mod 7, 6 is also the order of this group. This is because it is the first k that is 1 mod p, which is the order of the group. And since our group has 6 elements, 10=3 mod 7 is a primitive root of our group.
If 10 is a primitive root of module p, then all other fractions of the form a/p (truncated and a must not be a multiple of 7) also have the maximum period length and their periodic number sequence is the same. It is only shifted cyclically.
1/7=0.142857...
2/7=0.285714...
3/7=0.428571...
4/7=0.571428...
5/7=0.714285...
6/7=0.857142...
Incidentally, I treated my pupils to the following song on the last day of class: 142857.
Of course I will ask them right after the vacations whether they still know the result of 1 divided by 7. And I hope you will never forget it either. Incidentally, the prince of mathematics, Karl Friedrich Gauss, also dealt with this topic in great detail and even created tables that could be used to determine the periods of very unusual fractions. Bear in mind that he did not yet have computers at his disposal.