
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
12-11-2024 - Linear Algebra - kernel and image [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_080)
Kernel and image of linear applications
Kernel of linear applications
The kernel of linear applications is a fundamental concept to understand the properties of linear transformations between vector spaces. The core of linear applications is also called kernel
Definition of the core of a linear transformation
Suppose we have a linear transformation

where V and W are vector spaces.
The kernel of T is given as follows
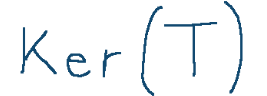
(Ker derives from the word kernel)
is defined as the set of all vectors in V that are sent to the null vector of W via T.
Algebraically it is written as follows:
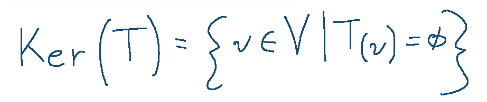
In other words, we can say that the kernel T is the set of all vectors of V that, after the application of T, are nullified.
Image of linear applications
The image of a linear application is a concept that is used to understand how a linear transformation acts on the elements of a vector space.
Let's now try to define what the image of a linear transformation is.
Suppose that

is a linear transformation from a vector space V to a vector space W.
The image of T is given as follows:
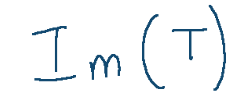
The image T is defined as the set of all vectors in W that can be obtained by applying T to some vector of V.
In other words we can say that the image of T is the set of values that T reaches when applied to all vectors.
Considerations:
The image of a linear transformation is always a vector subspace of W.
The image of T provides information on the surjectivity of the transformation because if Im(T) = W then T is surjective. This means that every vector in W is reachable from a vector in V via T
The size of the image of T indicates the number of "independent directions" in W reachable via T.
Conclusions
The kernel and the image of a linear application are useful for understanding two fundamental aspects of a linear transformation:
-The kernel indicates which vectors of the starting space V are cancelled by the transformation, i.e. transformed into the null vector in the target space W
-The image represents all the vectors of the target space W that can be reached by applying the transformation to some vector of V
Question
Second kernel and image of linear applications are starting to be difficult concepts to understand in the context of linear algebra, is this the case for you too?

[ITALIAN]
12-11-2024 - Algebra lineare - nucleo e immagine [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_080)
Nucleo e immagine delle applicazioni lineari
Nucleo delle applicazioni lineari
Il nucleo delle applicazioni lineari è un concetto fondamentale per comprendere le proprietà delle trasformazioni lineari tra spazi vettoriali. Il nucleo delle applicazioni lineari è detto anche kernel
Definizione del nucleo di una trasformazione lineare
Supponiamo di avere una trasformazione lineare

dove V e W sono spazi vettoriali.
Il nucleo di T viene indicato come segue
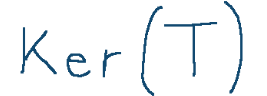
(Ker deriva appunto dalla parola kernel)
è definito come l'insieme di tutti i vettori in V che vengono mandati nel vettore nullo di W tramite T.
Algebricamente si scrive come segue:
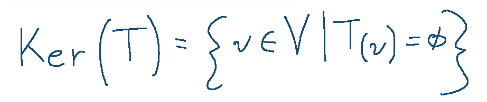
Possiamo dire in altre parole che il nucleo T è l’insieme di tutti i vettori di V che, dopo l’applicazione di T, risultano annullati.
Immagine delle applicazioni lineari
L’immagine di un’applicazione lineare è un concetto che serve per capire come una trasformazione lineare agisca sugli elementi di uno spazio vettoriale.
Proviamo ora a definire cosa è l’immagine di una trasformazione lineare.
Supponiamo che

sia una trasformazione lineare da uno spazio vettoriale V a uno spazio vettoriale W.
L’immagine di T viene indicata come segue:
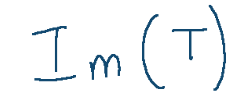
L’immagine T è definita come l’insieme di tutti i vettori in W che possono essere ottenuti applicando T a qualche vettore di V.
In altre parole possiamo dire che l’immagine di T è l’insieme dei valori che T raggiunge quando applicata a tutti i vettori.
Considerazioni:
L’immagine di una trasformazione lineare è sempre un sottospazio vettoriale di W.
L'immagine di T fornisce informazioni sulla suriettività della trasformazione perché se Im(T) = W allora T è suriettiva. QUesto significa che ogni vettore in W è raggiungibile da un vettore in V tramite T
La dimensione dell'immagine di T indica il numero di "direzioni indipendenti" in W raggiungibili tramite T.
Conclusioni
Il nucleo e l’immagine di un'applicazione lineare servono per comprendere due aspetti fondamentali di una trasformazione lineare:
-Il nucleo indica quali vettori dello spazio di partenza V vengono annullati dalla trasformazione, ossia trasformati nel vettore nullo nello spazio di arrivo W
-L'immagine rappresenta tutti i vettori dello spazio di arrivo W che possono essere raggiunti applicando la trasformazione a qualche vettore di V
Domanda
Secondo nucleo e immagine delle applicazioni lineari iniziano ad essere concetti difficili da comprendere nell'ambito dell'algebra lineare, anche per voi è così?
THE END


