
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
17-02-2025 - Analytic Geometry - Affine Subspaces [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_69)
Affine Subspaces
In analytical geometry, affine subspaces are sets of points that generalize the concept of line and plane in Euclidean space. They can be seen as translations of vector subspaces and maintain an affine but not vectorial structure.
Definition
An affine subspace A of a vector space R^n is a set of the following form:
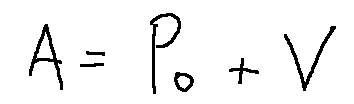
Where:
-P0 is a fixed point in the space (called reference point or also base point)
-V is a vector subspace of R^n (called direction of the affine subspace)
The mutual position of affine subspaces is quite similar to that of vector subspaces, but there is an important difference, because,
contrary to what happens with vector subspaces, affine subspaces may not intersect.
Pills on affine subspaces
-The point: an affine subspace of dimension 0 is a single point 𝑃0.
-Affine line: a line in the space is an affine subspace of dimension 1, and is defined as:
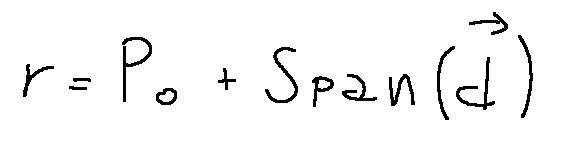
Exercise
Let's now take a parametric form, here it is:
Let's now try to understand which of the following parametric forms represents a line parallel to the line with shape parametric
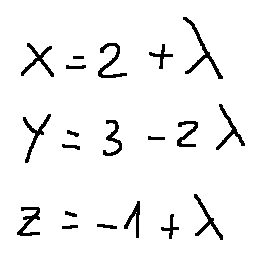
in space?
Here are four shapes, one of which is the parallel line.
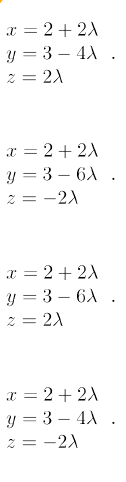
Step 01
First we determine the director vector of the given line
The director vector is obtained from the coefficients of λ:
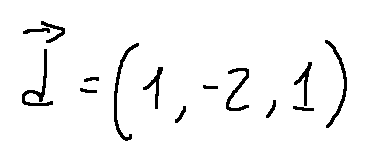
Step 02
We compare the director vectors of the four options
first line
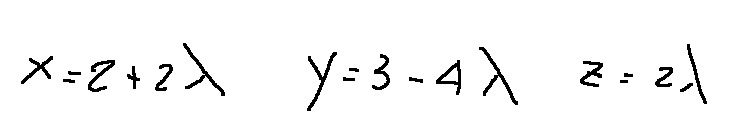
The director vector is:
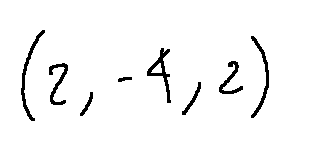
second line
Following the previous procedure we will have that the director vector in this case is:
(2,-6,-2)
Third line
Following the procedure that we followed with the first line, we will have that the director vector in this case is:
(2,-6,2)
Fourth line
Following the procedure that we followed with the first line, we will have that the director vector in this case is:
(2,-4,-2)
Step 03
Let's remember the conditions of parallelism. Two lines are parallel if their director vectors are scalar multiples.
The vector of the given line is
(1,−2,1)
So now we look for a vector that is a multiple of it:
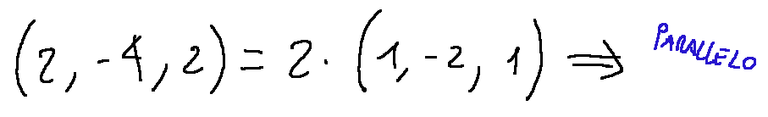
Result
The only line parallel to the given one, of the 4 proposed, is the first line, that is:
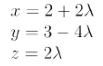
Conclusions
Affine subspaces are fundamental in analytical geometry because they allow us to describe lines, planes and hyperplanes in a more general way. They are used in:
-analytic geometry
-advanced geometric models
-linear algebra
-computer graphics
Question
Have you ever studied affine subspaces at school? Do you remember this topic, perhaps even covered in algebra class?

[ITALIAN]
17-02-2025 - Geometria analitica - I sottospazi affini [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_69)
I sottospazi affini
In geometria analitica, i sottospazi affini sono insiemi di punti che generalizzano il concetto di retta e piano nello spazio euclideo. Essi possono essere visti come traslazioni di sottospazi vettoriali e mantengono una struttura affine ma non vettoriale.
Definizione
Un sottospazio affine A di uno spazio vettoriale R^n è un insieme della seguente forma:
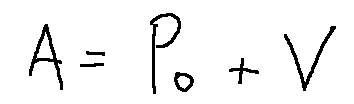
Dove:
-P0 è un punto fissato nello spazio (chiamato punto di riferimento o anche punto base)
-V è un sottospazio vettoriale di R^n (detto direzione del sottospazio affine)
La mutua posizione dei sottospazi affini è abbastanza simile a quella dei sottospazi vettoriali, ma c’è un’importante differenza, perché,
contrariamente a quanto succede con i sottospazi vettoriali, i sottospazi affini possono non intersecarsi.
Pillole sui sottospazi affini
-Il punto: un sottospazio affine di dimensione 0 è un singolo punto 𝑃0.
-Retta affine: una retta nello spazio è un sottospazio affine di dimensione 1, ed è definita come:
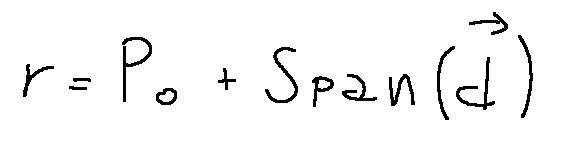
Esercizio
Prendiamo ora una forma parametrica, eccola riportata qui sotto:
Proviamo ora a capire quali delle seguenti forme parametriche rappresenta una retta parallela alla retta con forma parametrica
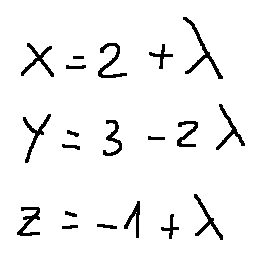
nello spazio?
Qui di seguito quattro forme di cui una è la retta parallela.
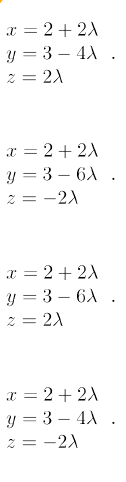
Passo 01
Per prima cosa determiniamo il vettore direttore della retta data
Il vettore direttore è ottenuto dai coefficienti di λ:
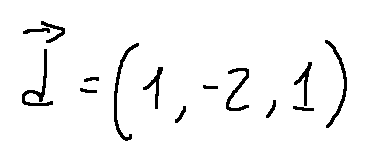
Passo 02
Confrontiamo i vettori direttori delle quattro opzioni
prima retta
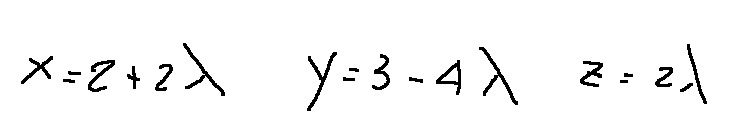
Il vettore direttore è:
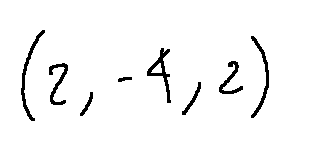
seconda retta
Seguendo il procedimento di prima avremo che il vettore direttore in questo caso è:
(2,-6,-2)
Terza retta
Seguendo il procedimento che abbiamo seguito con la prima retta avremo che il vettore direttore in questo caso è:
(2,-6,2)
Quarta retta
Seguendo il procedimento che abbiamo seguito con la prima retta avremo che il vettore direttore in questo caso è:
(2,-4,-2)
Passo 03
Ricordiamo le condizioni di parallelismo. Due rette sono parallele se i loro vettori direttori sono multipli scalari.
Il vettore della retta data è
(1,−2,1)
Quindi ora cerchiamo un vettore che sia un suo multiplo:
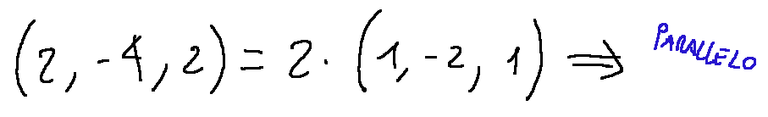
Risultato
L'unica retta parallela a quella data, delle 4 proposte, è la prima retta, ovvero:
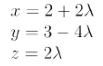
Conclusioni
I sottospazi affini sono fondamentali in geometria analitica perché permettono di descrivere rette, piani e iperpiani in modo più generale. Sono utilizzati in:
-geometria analitica
-modelli geometrici avanzati
-algebra lineare
-grafica computerizzata
Domanda
Avete mai studiato a scuola i sottospazi affini? Ricordate questo argomento, magari svolto anche durante le lezioni di algebra?
THE END


