
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
20-11-2024 - Analytic Geometry - Eigenvalues and Eigenvectors [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_73)
Eigenvalues and Eigenvectors
Description
Eigenvectors and eigenvalues of endomorphisms can be thought of as the directions and the factors of lengthening, or shortening, of an endomorphism, respectively.
With eigenvalues and eigenvectors, linear transformations represented by matrices can be analyzed. These concepts help to understand how a transformation acts on a vector space.
Definition
Let A be a square matrix of dimension n x n, and let v be a non-zero vector of dimension n. If there exists a scalar such that...
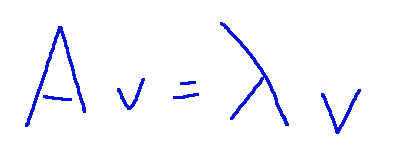
then:
-λ is called the eigenvalue of A
-v is called the eigenvector associated with the eigenvalue
Geometric concept
-Eigenvectors are invariant directions of the transformation A, i.e. directions in space that are not "tilted" by the transformation.
-Eigenvalues represent the scaling factor along those directions.
Example
Find an eigenvector of the following matrix relative to the corresponding eigenvalue (λ)
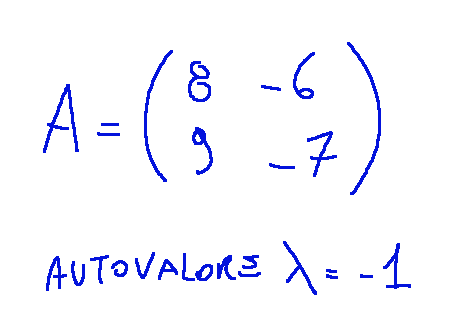
-01
Write A - λI
The matrix A - λI is calculated by subtracting λ from the diagonal of A
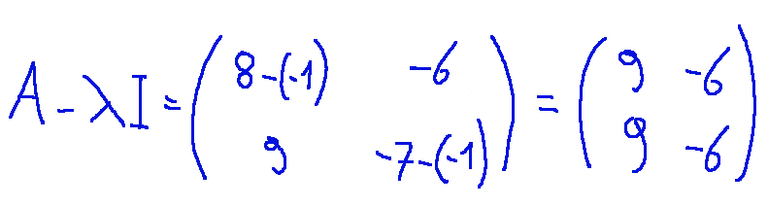
-02 Let us now solve the system (A - λI) v = 0 so…
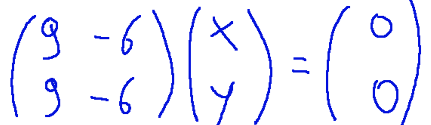
This leads back to the following system linear
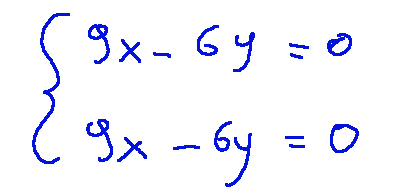
Since the equations are identical we can simplify by choosing just one:
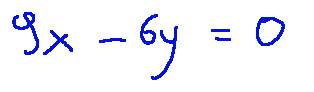
-03
Now let's find the relationship between x and y by simplifying the equation.
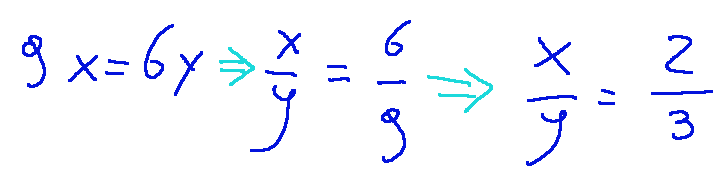
so we get the value of x
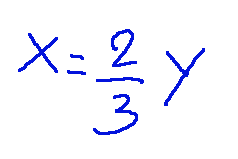
-04
To get an eigenvector we need to assign an arbitrary value to y. Warning: the value must not be 0.
In this case we choose that y = 3.
As a consequence we will have that:
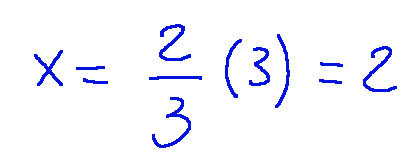
The associated eigenvector is:
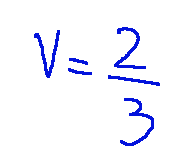
Result
A eigenvector relative to the eigenvalue λ = -1 is…
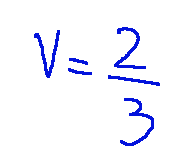
Conclusions
Eigenvalues and eigenvectors are fundamental concepts in linear algebra and analytic geometry, closely related to linear transformations.
Question
Do you remember studying eigenvalues and eigenvectors at school?

[ITALIAN]
20-11-2024 - Geometria analitica - Autovalori e autovettori [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_73)
Autovalori e autovettori
Descrizione
Gli autovettori e gli autovalori degli endomorfismi possono essere pensati rispettivamente come le direzioni e i fattori di allungamento, o di accorciamento, di un endomorfismo.
Con gli autovalori e autovettori si possono analizzare trasformazioni lineari rappresentate da matrici. Questi concetti aiutano a comprendere come una trasformazione agisce su uno spazio vettoriale.
Definizione
Sia A una matrice quadrata di dimensione n x n, e sia v un vettore non nullo di dimensione n. Se esiste uno scalare tale che...
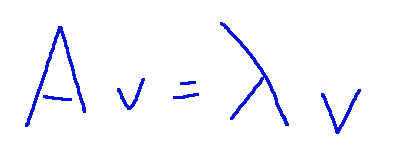
allora:
-λ è detto autovalore di A
-v è detto autovettore associato all’autovalore
Concetto geometrico
-Gli autovettori sono direzioni invarianti della trasformazione A, cioè direzioni nello spazio che non vengono "inclinate" dalla trasformazione.
-Gli autovalori rappresentano il fattore di scalatura lungo quelle direzioni.
Esempio
Trovare un autovettore della seguente matrice relativamente al corrispondente autovalore (λ)
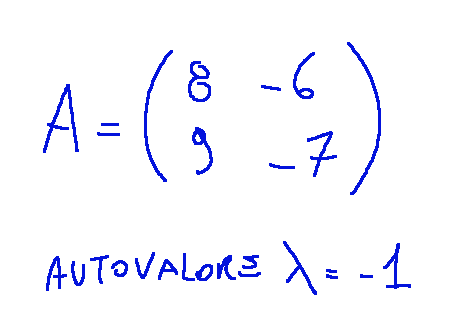
-01
Scrivere A - λI
La matrice A - λI si calcola sottraendo λ dalla diagonale di A
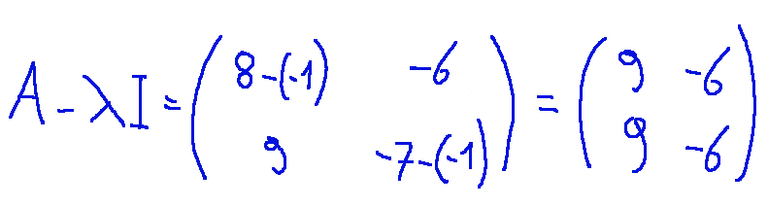
-02
Risolviamo ora il sistema (A - λI) v = 0
quindi…
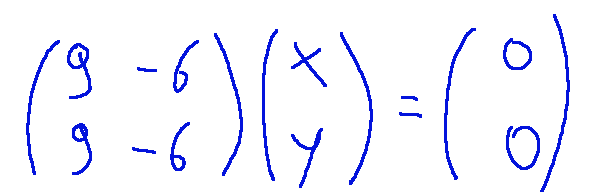
Questo si riconduce al seguente sistema lineare
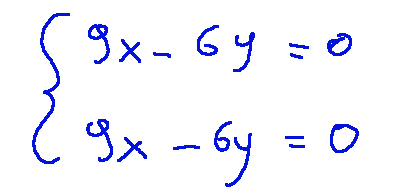
Siccome le equazioni sono identiche possiamo semplificare scegliendone una sola:
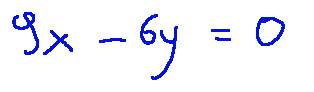
-03
Troviamo ora la relazione tra x e y semplificando l’equazione.
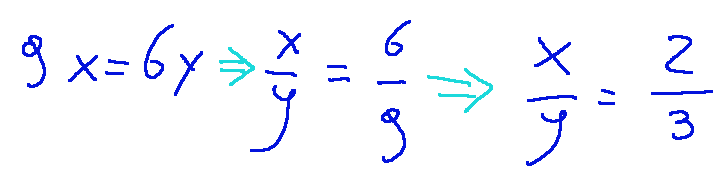
quindi otteniamo il valore di x
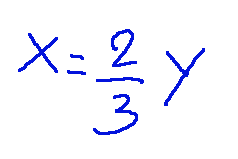
-04
Per ottenere un autovettore dobbiamo assegnare un valore arbitrario a y. Attenzione il valore non deve essere 0.
In questo caso scegliamo che y = 3.
Di conseguenza avremo che:
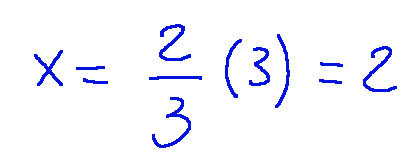
L'autovettore associato è:
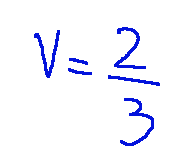
Risultato
Un autovettore relativo all’autovalore λ = -1 è…
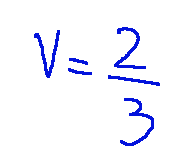
Conclusioni
Gli autovalori e gli autovettori sono concetti fondamentali in algebra lineare e geometria analitica, strettamente legati alle trasformazioni lineari.
Domanda
Ricordato di aver studiato a scuola gli autovalori e autovettori?
THE END


